本人这次侥幸省1,特做题解复习,哈哈哈…

1.进制转换(5分):
问题描述:

直接计算 2 + 2 * 9 + 2 * 9 * 9 * 9
答案: 1478
2.顺子日期(5分)

这题有争议: 主要在于0等不能开头:如 20220121
本人认为0不能作为开头 (因为例题中20220123 说明的顺子为123并不是012):
所以顺子日期有: 20220123 20221123 20221230 20221231
答案 :4
3.刷题统计(10分)

解题思路:
考虑 a=1,b=1,n=1e18 情况,不能一天一天计算,会超时5 * a+2 * b 为一周的刷题量,先除法计算多少周,剩余的天数一直减就是了if (n <= 0)break; 要放在第一位参考代码:
#include<iostream>using namespace std;int main(){ long long a, b, n; cin >> a >> b >> n; long long day = 0; long long t = n / (5 * a + 2 * b); day += t * 7; //先算多少周 n = n % (5 * a + 2 * b); for (int i = 1; i <= 7; i++) { //再算天数 if (n <= 0)break; if (i > 5)n -= b; else n -= a; day++; } cout << day; return 0;}4.修剪灌木(10分)

思路:
对于每一个点都需要考虑 距离1端点的距离 和 n端点的距离因为来回剪,所以需要将距离 * 2再取两者大值即可最后特判 1的情况参考代码:
#include<iostream>using namespace std;int main(){ int n; cin >> n; if (n == 1) { cout << 1 << endl; return 0; } for (int i = 1; i <= n; i++) { cout << max(2 * (i - 1), 2 * (n - i))<< endl; }}5.X进制减法(15分)


算法 : 简单的贪心
先分析一下题干的65是怎么出来的:
第一数位每一个数代表的必然是1第二数位是由第一数位的二进制上来的,所以第二数位每一个数代表的是2第三数位是由第二数位十进制进位上来的,所以第三数位每一个数代表的是2 * 10 = 20所以 : X(321) = 3 * 20 + 2 * 2 + 1 * 1 = 65;
参考代码:
#include<iostream>using namespace std;const int N = 1e5 + 10,MOD=1e9+7;int a[N], b[N];int n, ma, mb;int main(){cin >> n;cin >> ma;for (int i = ma - 1; i >= 0; i--)cin >> a[i];cin >> mb;for (int i = mb - 1; i >= 0; i--)cin >> b[i];long long t = 1; //到每一个的底数long long ans=0;for (int i = 0; i < ma; i++) {int c = max(a[i], b[i]) + 1; //贪心取得最小的进制if (c < 2)c = 2; //最小为2进制ans = (ans+(a[i] - b[i]) * t)%MOD;t = (t * c) % MOD; }cout<<ans;}6.统计子矩阵(15分)

算法 :二维前缀和
注意 : 理论上朴素前缀和,在100%的数据上会超时 ,需要优化,只需不重复计算子矩阵就行
#include<iostream>using namespace std;const int N = 510;int g[N][N];int n, m, k;int main(){cin >> n >> m >> k;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> g[i][j];g[i][j] += g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1];}}/*for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << g[i][j] << " ";}cout << endl;}*/int ans = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {for (int x = i; x <= n; x++) {for (int y = j; y <= m; y++) {if (g[x][y] - g[x][j - 1] - g[i - 1][y] + g[i - 1][y - 1] <= k)ans++;}}}}cout << ans;}7.积木画(20分)

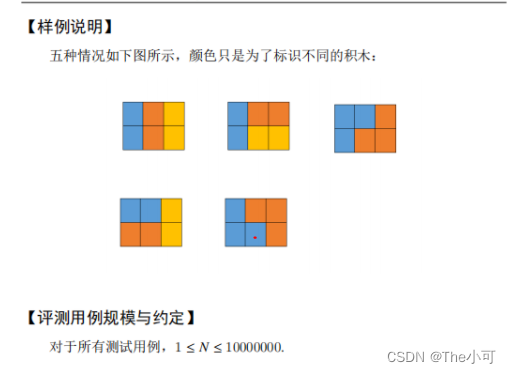
算法 : 动态规划
思路 :
转换方程 : dp[i] 由 dp[i-1] , dp[i-2], dp[i-3] 状态转换过来
由dp[i-1] 转到 dp[i] 只有一种可能
所以 dp[i] = dp[i-1] * 1
由dp[i-2] 转到 dp[i] 只有一种可能(需要排除1中的情况)
所以 dp[i] = dp[i-2] * 1
由 dp[i-3] 转到 dp[i] 有两种可能(需要排除1,2 的情况)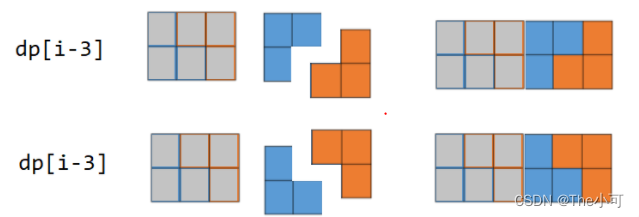
所以 dp[i] = dp[i-3] * 2
综上 : dp[i] = dp[i-1] + dp[i-2] +dp[i-3] * 2
初始状态 : dp[0] = 1 , dp[1] = 1 , dp[2] = 2
最终状态转移方程 : dp[i] = (dp[i - 1] + dp[i - 2] + dp[i - 3] * 2)%MOD;
参考代码:
#include <iostream>using namespace std;const int N = 1e7 + 4, MOD = 1000000007;int dp[N]; //dp[i]表示长度为i有dp[i]个拼法int n;int main() { cin >> n; dp[0] = 1; dp[1] = 1; dp[2] = 2; for (int i = 3; i <= n; i++) { dp[i] = (dp[i - 1] + dp[i - 2] + dp[i - 3] * 2)%MOD; } cout << dp[n] ; return 0;}8.扫雷(20分)

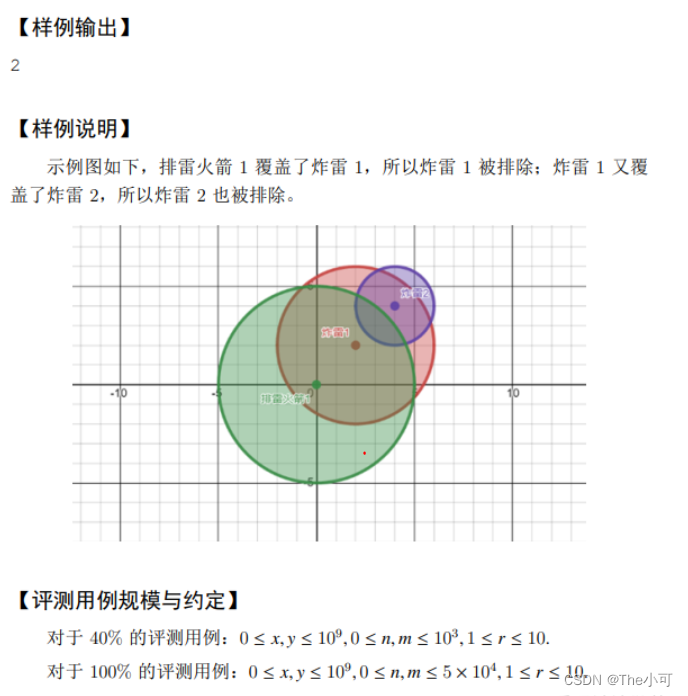
算法 :DFS
思路 :
被引爆的地雷可以认为是一颗排雷火箭每颗排雷火箭引爆,都遍历一下全部地雷,若在范围内,则将这颗雷引爆引爆了的雷需要标记一下,防止重复引爆参考代码:
#include <iostream>using namespace std;const int N = 50010;struct Node { int x, y, r;};int n, m,ans=0;Node mine[N];bool visited[N];Node rocket[N];bool compare(Node a, Node b) { long xx = (a.x-b.x) * (a.x - b.x); long yy = (a.y-b.y) * (a.y - b.y); return sqrt(xx+yy) <= a.r;}void boom(Node node) { for (int i = 0; i < n; i++) { if (visited[i])continue; if (compare(node, mine[i])) { visited[i] = true; ans++; boom(mine[i]); } }}int main() { cin >> n >> m; int x, y, r; for (int i = 0; i < n; i++) { cin >> x >> y >> r; mine[i] = { x,y,r }; } for (int i = 0; i < m; i++) { cin >> x >> y >> r; rocket[i] = { x,y,r }; } for (int i = 0; i < m; i++) { boom(rocket[i]); } cout << ans; return 0;}9.李白打酒加强版


算法 : 动态规划
状态表示:f[i][j][k] 表示访问前i个位置时,恰好访问j个店并且酒量恰好为k的时候的方案数;
状态转移:
看花 : f[i][j][k] = f[i-1][j-1][k+1]遇店 : f[i][j][k] = f[i-1][j][k/2];起始状态 :f[0][0][2] 刚开始2斗酒
注意:
看花时,需要保证 j>1 (不可能在上一次zhi前看完了花,这次还看花)看店时 需要保证这是酒的数量是偶数,因为加倍永远是偶数参考代码:
#include <iostream>using namespace std;const int N = 110,MOD = 1e9+7;int n, m;int f[2*N][N][N]; //f[i][j][k] 表示在第i个位置(共有 n+m个位置),遇到j个花,目前还剩 k斗酒int main() { cin >> n >> m; f[0][0][2] = 1; for (int i = 1; i <= n + m; i++) { for (int j = 0; j <= m; j++) { for (int k = 0; k <= m; k++) { //酒的最大数量为m,如果大于m,就算后面的全是花也喝不完酒 //遇到花 if(j>=1) f[i][j][k] =f[i - 1][j - 1][k + 1]; //遇到酒 if (k % 2 == 0) { // f[i][j][k] = (f[i][j][k]+f[i - 1][j][k / 2])%MOD; } } } } cout << f[n + m - 1][m - 1][1]; return 0;}10.砍竹子


先做前面的,没做出来!!!!
最后总结:
蓝桥杯已经变了,不再是以前的暴力杯了,考验的更是思维,dfs和动态规划将成为常客。以后的小伙伴要多刷题,刷题,刷题!!!