
目录
1. 二叉树的中序遍历 ★★
2. 平衡二叉树 ★★
3. 二叉树中的最大路径和 ★★★
? 每日一练刷题专栏
C/C++ 每日一练 专栏
Python 每日一练 专栏
1. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回它的 中序 遍历。
示例 1:
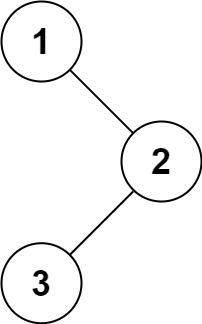
输入:root = [1,null,2,3]输出:[1,3,2]
示例 2:
输入:root = []输出:[]
示例 3:
输入:root = [1]输出:[1]
示例 4:
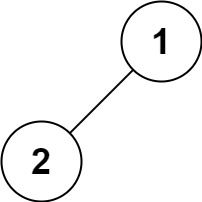
输入:root = [1,2]输出:[2,1]
示例 5:
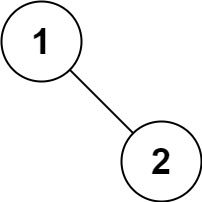
输入:root = [1,null,2]输出:[1,2]
提示:
树中节点数目在范围[0, 100] 内-100 <= Node.val <= 100进阶:递归算法很简单,你可以通过迭代算法完成吗?
代码:
#include <stdio.h>#include <stdlib.h>#define null INT_MINstruct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}};void traverse(struct TreeNode *node, int *result, int *count){ if (node == NULL) { return; } traverse(node->left, result, count); result[*count] = node->val; (*count)++; traverse(node->right, result, count);}int* inorderTraversal(struct TreeNode *root, int *returnSize){ if (root == NULL) { *returnSize = 0; return NULL; } int count = 0; int *result = (int*)malloc(5000 * sizeof(int)); traverse(root, result, &count); *returnSize = count; return result;}TreeNode* createTree(int nums[], int size = 0, int index = 0) { if (index >= size || nums[index] == null) { return NULL; } TreeNode *node = (TreeNode*)malloc(sizeof(TreeNode)); node->val = nums[index]; node->left = createTree(nums, size, 2 * index + 1); node->right = createTree(nums, size, 2 * index + 2); return node;}int main() { int nums[] = {1, null, 2, null, null, 3}; int size = sizeof(nums) / sizeof(nums[0]); TreeNode *root = createTree(nums, size); int count = 0; int *result = inorderTraversal(root, &count); for (int i = 0; i < count; i++) { printf("%d ", result[i]); } printf("\n"); return 0;}输出:
1 3 2
原题用C语言,改用C++代码如下:
#define null INT_MIN#include <iostream>#include <vector>#include <stack>using namespace std;struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}};TreeNode* buildTree(vector<int> arr, int i = 0) { if (i >= arr.size() || arr[i] == null) { return NULL; } TreeNode* root = new TreeNode(arr[i]); if (root == NULL) return NULL; root->left = buildTree(arr, 2 * i + 1); root->right = buildTree(arr, 2 * i + 2); return root;}class Solution{private: void traversal(TreeNode *root, vector<int> &ret) { if (root != NULL) { traversal((*root).left, ret); ret.push_back(root->val); traversal((*root).right, ret); } }public: vector<int> inorderTraversal(TreeNode *root) { vector<int> res; traversal(root, res); return res; }};int main() {Solution s; vector<int> root = {1, null, 2, null, null, 3}; TreeNode* tree = buildTree(root); for (auto val: s.inorderTraversal(tree))cout << val << " ";cout << endl; root = {}; tree = buildTree(root); for (auto val: s.inorderTraversal(tree))cout << val << " ";cout << endl; root = {1}; tree = buildTree(root, 0); for (auto val: s.inorderTraversal(tree))cout << val << " ";cout << endl; return 0;}进阶1:
创建和遍历都不用递归法,其中创建时空节点下的“空”位置就不用再标注出来了,比如:递归创建时使用数组{1,null,2,null,null,3},直接{1,null,2,3}时节点Node(3)会被丢弃。
#include <bits/stdc++.h>#define null INT_MINusing namespace std;struct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}};TreeNode* buildTree(vector<int>& nums){ if (nums.empty()) return nullptr;TreeNode *root = new TreeNode(nums.front()); queue<TreeNode*> q; q.push(root); int i = 1; while(!q.empty() && i < nums.size()) { TreeNode *cur = q.front(); q.pop(); if(i < nums.size() && nums[i] != null) { cur->left = new TreeNode(nums[i]); q.push(cur->left); } i++; if(i < nums.size() && nums[i] != null) { cur->right = new TreeNode(nums[i]); q.push(cur->right); } i++; } return root;}void inorderTraversal(TreeNode* root) { stack<TreeNode*> nodes; TreeNode* p = root; while (p != NULL || !nodes.empty()) { if (p != NULL) { nodes.push(p); p = p->left; } else { p = nodes.top(); nodes.pop(); cout << p->val << " "; p = p->right; } } cout << endl;}int main() { vector<int> nums = {1,null,2,3}; TreeNode *root = buildTree(nums); inorderTraversal(root);nums = {3,9,20,null,null,15,7};root = buildTree(nums); inorderTraversal(root);nums = {1,2,2,3,3,null,null,4,4};root = buildTree(nums); inorderTraversal(root); return 0;}输出:
1 3 2
9 3 15 20 7
4 3 4 2 3 1 2
进阶2:
遍历结果存入数组,再把数组转成某种样式的字符串形式
#include <bits/stdc++.h>#define null INT_MINusing namespace std;struct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}};TreeNode* buildTree(vector<int>& nums){ if (nums.empty()) return nullptr;TreeNode *root = new TreeNode(nums.front()); queue<TreeNode*> q; q.push(root); int i = 1; while(!q.empty() && i < nums.size()) { TreeNode *cur = q.front(); q.pop(); if(i < nums.size() && nums[i] != null) { cur->left = new TreeNode(nums[i]); q.push(cur->left); } i++; if(i < nums.size() && nums[i] != null) { cur->right = new TreeNode(nums[i]); q.push(cur->right); } i++; } return root;}vector<int> inorderTraversal(TreeNode* root) { vector<int> res; stack<TreeNode*> nodes; TreeNode* p = root; while (p != NULL || !nodes.empty()) { if (p != NULL) { nodes.push(p); p = p->left; } else { p = nodes.top(); nodes.pop(); res.push_back(p->val); p = p->right; } } return res;}string vectorToString(vector<int> vect) { stringstream ss;ss << "["; for (int i = 0; i < vect.size(); i++){ ss << (vect[i] == null ? "null" : to_string(vect[i])); ss << (i < vect.size() - 1 ? ", " : "]"); } return ss.str();}int main() { vector<int> nums = {1,null,2,3}; TreeNode *root = buildTree(nums); nums = inorderTraversal(root); cout << vectorToString(nums) << endl;nums = {3,9,20,null,null,15,7};root = buildTree(nums); nums = inorderTraversal(root); cout << vectorToString(nums) << endl;nums = {1,2,2,3,3,null,null,4,4};root = buildTree(nums); nums = inorderTraversal(root); cout << vectorToString(nums) << endl; return 0;}输出:
[1, 3, 2]
[9, 3, 15, 20, 7]
[4, 3, 4, 2, 3, 1, 2]
2. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
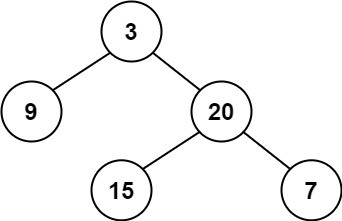
输入:root = [3,9,20,null,null,15,7]输出:true
示例 2:
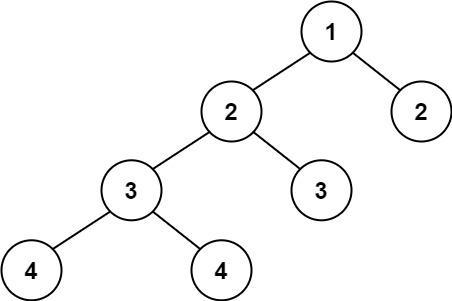
输入:root = [1,2,2,3,3,null,null,4,4]输出:false
示例 3:
输入:root = []输出:true
提示:
树中的节点数在范围[0, 5000] 内-10^4 <= Node.val <= 10^4代码: 递归法
#include <bits/stdc++.h>#define null INT_MINstruct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}};class Solution{public: int depth(TreeNode *root) { if (root == NULL) return 0; int left = depth(root->left); int right = depth(root->right); return fmax(left, right) + 1; } bool isBalanced(TreeNode *root) { if (root == NULL) return true; if (abs(depth(root->left) - depth(root->right)) > 1) return false; else return isBalanced(root->left) && isBalanced(root->right); }};TreeNode* createTree(int nums[], int size = 0, int index = 0) { if (index >= size || nums[index] == null) { return NULL; } TreeNode *node = (TreeNode*)malloc(sizeof(TreeNode)); node->val = nums[index]; node->left = createTree(nums, size, 2 * index + 1); node->right = createTree(nums, size, 2 * index + 2); return node;}int main() { int nums1[] = {3,9,20,null,null,15,7}; int size = sizeof(nums1) / sizeof(nums1[0]); TreeNode *root = createTree(nums1, size); Solution s; printf("%d\n", s.depth(root->left)); printf("%d\n", s.depth(root->right)); printf("%s\n", s.isBalanced(root) ? "true" : "false"); int nums2[] = {1,2,2,3,3,null,null,4,4}; size = sizeof(nums2) / sizeof(nums2[0]); root = createTree(nums2, size); printf("%d\n", s.depth(root->left)); printf("%d\n", s.depth(root->right)); printf("%s\n", s.isBalanced(root) ? "true" : "false"); root = createTree(NULL); printf("%s\n", s.isBalanced(root) ? "true" : "false"); return 0;}输出:
1
2
true
3
1
false
true
进阶: statck / DFS
#include <bits/stdc++.h>#define null INT_MINusing namespace std;struct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}};TreeNode* buildTree(vector<int>& nums){ if (nums.empty()) return nullptr;TreeNode *root = new TreeNode(nums.front()); queue<TreeNode*> q; q.push(root); int i = 1; while(!q.empty() && i < nums.size()) { TreeNode *cur = q.front(); q.pop(); if(i < nums.size() && nums[i] != null) { cur->left = new TreeNode(nums[i]); q.push(cur->left); } i++; if(i < nums.size() && nums[i] != null) { cur->right = new TreeNode(nums[i]); q.push(cur->right); } i++; } return root;}bool isBalanced(TreeNode* root) { stack<TreeNode*> s; TreeNode* p = root; TreeNode* last = nullptr; unordered_map<TreeNode*, int> um; int height = 0; while (p != nullptr || !s.empty()) { while (p != nullptr) { s.push(p); um[p] = ++height; p = p->left; } p = s.top(); if (p->right == nullptr || last == p->right) { int leftHeight = um[p->left]; int rightHeight = um[p->right]; if (abs(leftHeight - rightHeight) > 1) { return false; } height = max(leftHeight, rightHeight); s.pop(); last = p; p = nullptr; } else { p = p->right; } } return true;}int main() { vector<int> nums = {3,9,20,null,null,15,7}; TreeNode *root = buildTree(nums); cout << (isBalanced(root) ? "true" : "false") << endl; nums = {1,2,2,3,3,null,null,4,4}; root = buildTree(nums); cout << (isBalanced(root) ? "true" : "false") << endl; nums = {}; root = buildTree(nums); cout << (isBalanced(root) ? "true" : "false") << endl; return 0;}输出:
true
false
true
3. 二叉树中的最大路径和
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
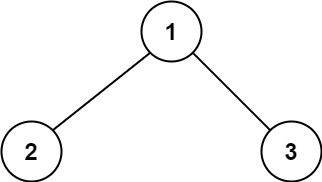
输入:root = [1,2,3]输出:6解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
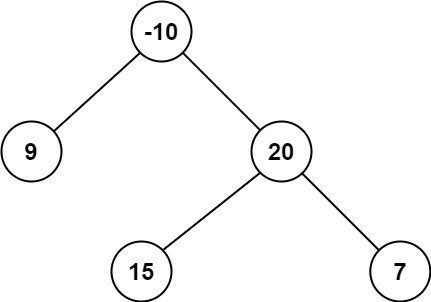
输入:root = [-10,9,20,null,null,15,7]输出:42解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
树中节点数目范围是[1, 3 * 10^4]-1000 <= Node.val <= 1000代码:
#include <bits/stdc++.h>#define null INT_MINusing namespace std;struct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}};class Solution{public: int maxPathSum(TreeNode *root) { if (!root) return 0; vector<TreeNode *> ss; unordered_map<TreeNode *, int> val; ss.push_back(root); int len = 1; queue<TreeNode *> q{{root}}; while (!q.empty()) { TreeNode *t = q.front(); q.pop(); //cout << t->val << endl; if (t->left) { len++; q.push(t->left); ss.push_back(t->left); } if (t->right) { len++; q.push(t->right); ss.push_back(t->right); } } int res = INT_MIN; while (len > 0) { TreeNode *node = ss[--len]; int ps = node->val; int s = ps; int ls = max(0, val[node->left]); int rs = max(0, val[node->right]); ps += max(ls, rs); val[node] = ps; s += ls + rs; res = max(s, res); } return res; }};TreeNode* buildTree(vector<int>& nums){ if (nums.empty()) return nullptr;TreeNode *root = new TreeNode(nums.front()); queue<TreeNode*> q; q.push(root); int i = 1; while(!q.empty() && i < nums.size()) { TreeNode *cur = q.front(); q.pop(); if(i < nums.size() && nums[i] != null) { cur->left = new TreeNode(nums[i]); q.push(cur->left); } i++; if(i < nums.size() && nums[i] != null) { cur->right = new TreeNode(nums[i]); q.push(cur->right); } i++; } return root;}int main(){ vector<int> nums = {1,2,3}; TreeNode *root = buildTree(nums); Solution s; cout << s.maxPathSum(root) << endl; nums = {-10,9,20,null,null,15,7}; root = buildTree(nums); cout << s.maxPathSum(root) << endl; return 0;}输出:
6
42
递归法:
#include <bits/stdc++.h>#define null INT_MINusing namespace std;struct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}};class Solution{public:int maxPathSum(TreeNode* root){ int maxSum = INT_MIN; maxPathSum(root, maxSum); return maxSum;}int maxPathSum(TreeNode* root, int& maxSum){ if (root == nullptr) return 0; int leftSum = max(0, maxPathSum(root->left, maxSum)); int rightSum = max(0, maxPathSum(root->right, maxSum)); int curSum = root->val + leftSum + rightSum; // 经过当前节点的最大路径和 maxSum = max(maxSum, curSum); // 更新最大路径和 return root->val + max(leftSum, rightSum);}};TreeNode* buildTree(vector<int>& nums){ if (nums.empty()) return nullptr;TreeNode *root = new TreeNode(nums.front()); queue<TreeNode*> q; q.push(root); int i = 1; while(!q.empty() && i < nums.size()) { TreeNode *cur = q.front(); q.pop(); if(i < nums.size() && nums[i] != null) { cur->left = new TreeNode(nums[i]); q.push(cur->left); } i++; if(i < nums.size() && nums[i] != null) { cur->right = new TreeNode(nums[i]); q.push(cur->right); } i++; } return root;}int main(){ vector<int> nums = {1,2,3}; TreeNode *root = buildTree(nums); Solution s; cout << s.maxPathSum(root) << endl; nums = {-10,9,20,null,null,15,7}; root = buildTree(nums); cout << s.maxPathSum(root) << endl; return 0;}? 每日一练刷题专栏
✨ 持续,努力奋斗做强刷题搬运工!
? 点赞,你的认可是我坚持的动力!
★ 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
 | C/C++ 每日一练 专栏 |
 | Python 每日一练 专栏 |