目录

1.创建二叉树节点

2.使用前序遍历创建二叉树

3.遍历二叉树 

3.1 前序遍历二叉树

3.2 中序遍历二叉树

3.3 后序遍历二叉树

4. 二叉树是否为空

5. 求二叉树的节点数

6.求二叉树的深度

完整代码

运行测试用例及截图

1.创建二叉树节点

typedef struct TreeNode {char data;//数据域TreeNode* Lchild;//左孩子TreeNode* Rchild;//右孩子}*Tree, TreeNode;

2.使用前序遍历创建二叉树

void CreateTree(Tree& T) {char x;cin >> x;if (x =='*') {T = NULL; return;}else {T = new TreeNode;T->data = x;CreateTree(T->Lchild);CreateTree(T->Rchild);}}

3.遍历二叉树 

3.1 前序遍历二叉树

void Pre_Traversal(const Tree& T) {if (T) {cout << T->data<<" ";Pre_Traversal(T->Lchild);Pre_Traversal(T->Rchild);}}

3.2 中序遍历二叉树

void Ino_Traversal(const Tree& T) {if (T) {Ino_Traversal(T->Lchild);cout << T->data<<" ";Ino_Traversal(T->Rchild);}}

3.3 后序遍历二叉树

void Pos_Traversal(const Tree& T) {if (T) {Pos_Traversal(T->Lchild);Pos_Traversal(T->Rchild);cout << T->data << " ";}}

4. 二叉树是否为空

bool TreeEmpty(const Tree& T) {if (T == NULL){cout << "该二叉树为空！"<<endl; return true;}else{cout << "该二叉树为不为空！"<<endl;return false;}}

5. 求二叉树的节点数

int TreeNodeCount(const Tree& T) {if (T == NULL)return 0;else if (T->Lchild == NULL && T->Rchild == NULL)return 1;elsereturn TreeNodeCount(T->Lchild) + TreeNodeCount(T->Rchild)+1;}

6.求二叉树的深度

int TreeDepth(const Tree& T) {if (T == NULL) return 0;else {int i = TreeDepth(T->Lchild);int j = TreeDepth(T->Rchild);return i > j ? i + 1 : j + 1;}}

完整代码

#include<iostream>using namespace std;typedef struct TreeNode {char data;//数据域TreeNode* Lchild;//左孩子TreeNode* Rchild;//右孩子}*Tree, TreeNode;//前序创建二叉树void CreateTree(Tree& T) {char x;cin >> x;if (x =='*') {T = NULL; return;}else {T = new TreeNode;T->data = x;CreateTree(T->Lchild);CreateTree(T->Rchild);}}//先序遍历void Pre_Traversal(const Tree& T) {if (T) {cout << T->data<<" ";Pre_Traversal(T->Lchild);Pre_Traversal(T->Rchild);}}//中序遍历void Ino_Traversal(const Tree& T) {if (T) {Ino_Traversal(T->Lchild);cout << T->data<<" ";Ino_Traversal(T->Rchild);}}//后序遍历void Pos_Traversal(const Tree& T) {if (T) {Pos_Traversal(T->Lchild);Pos_Traversal(T->Rchild);cout << T->data << " ";}}//二叉树是否为空bool TreeEmpty(const Tree& T) {if (T == NULL){cout << "该二叉树为空！"<<endl; return true;}else{cout << "该二叉树为不为空！"<<endl;return false;}}//求二叉树的节点数int TreeNodeCount(const Tree& T) {if (T == NULL)return 0;else if (T->Lchild == NULL && T->Rchild == NULL)return 1;elsereturn TreeNodeCount(T->Lchild) + TreeNodeCount(T->Rchild)+1;}//求二叉树的深度int TreeDepth(const Tree& T) {if (T == NULL) return 0;else {int i = TreeDepth(T->Lchild);int j = TreeDepth(T->Rchild);return i > j ? i + 1 : j + 1;}}int main(){Tree T;cout << "请按先序遍历的顺序创建二叉树，若其节点的左孩子或右孩子不存在则使用*代替！如：（ABD**E**CF**G**）" << endl;CreateTree(T);TreeEmpty(T);cout << "先序遍历的结果为：";Pre_Traversal(T) ;cout<< endl;cout << "中序遍历的结果为：";Ino_Traversal(T);cout << endl;cout << "后序遍历的结果为：";Pos_Traversal(T);cout << endl;cout << "该树的深度为："<< TreeDepth(T)<< endl;cout << "该树的节点数为：" << TreeNodeCount(T) << endl;system("pause");}

运行测试用例及截图

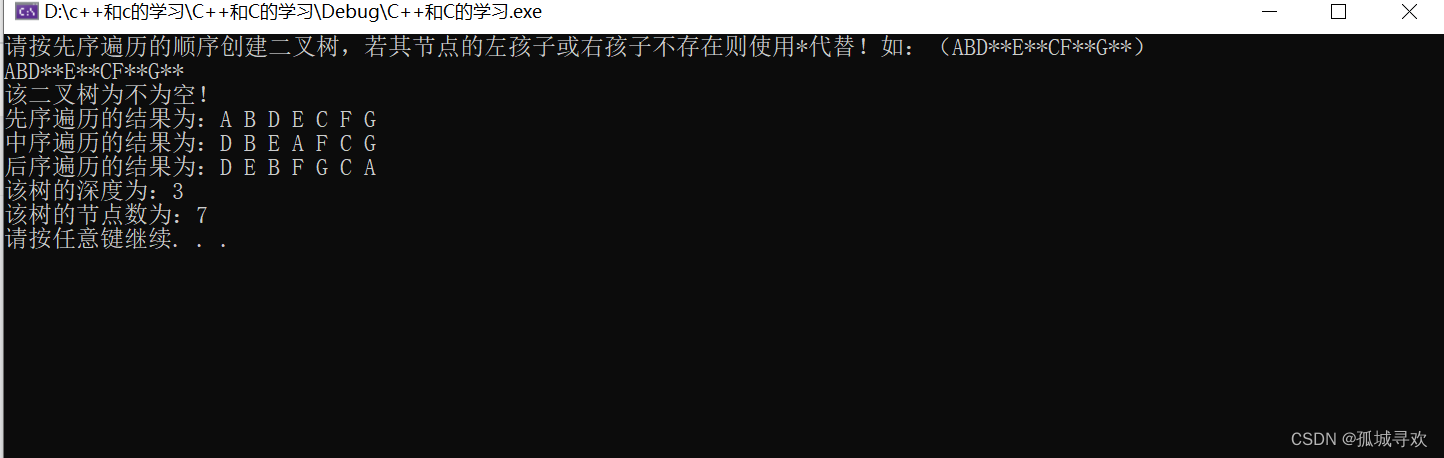
下图为测试用例： (ABD**E**CF**G**)

                        ​​​​​​​

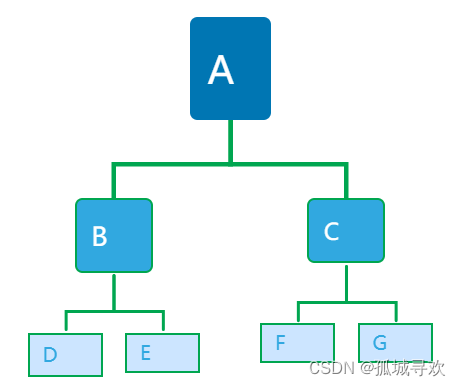
前序遍历：A B D E C F G

中序遍历：D B E A F C G

后序遍历：D E B F G C A

总节点数 ：7

树的深度：3 

运行截图如下：