?大家好,我是白晨,一个不是很能熬夜?,但是也想日更的人✈。如果喜欢这篇文章,点个赞?,关注一下?白晨吧!你的支持就是我最大的动力!???

文章目录
?前言?1.公式选择?2.实现难点解析?3.代码实现?后记
?前言
π π π 一直是一个备受数学界青睐的数字。从古至今,无数的学者都在努力探求着 π π π 精确值。?♂️从祖冲之到欧拉,?从圣经到《数理精蕴》,从东至西,历经几千年的发展,特别是在计算机发明之后,对于 π π π 的求解可以说是一日千里,现在计算到几十亿位以后已经不值得惊讶。
?这篇文章,白晨想带大家去了解利用计算机求解 π π π 的一种方法,其中涉及到 C++,链表,大数四则运算等知识点。我会尽可能详细的讲解每一个难点的实现。
题目参考:
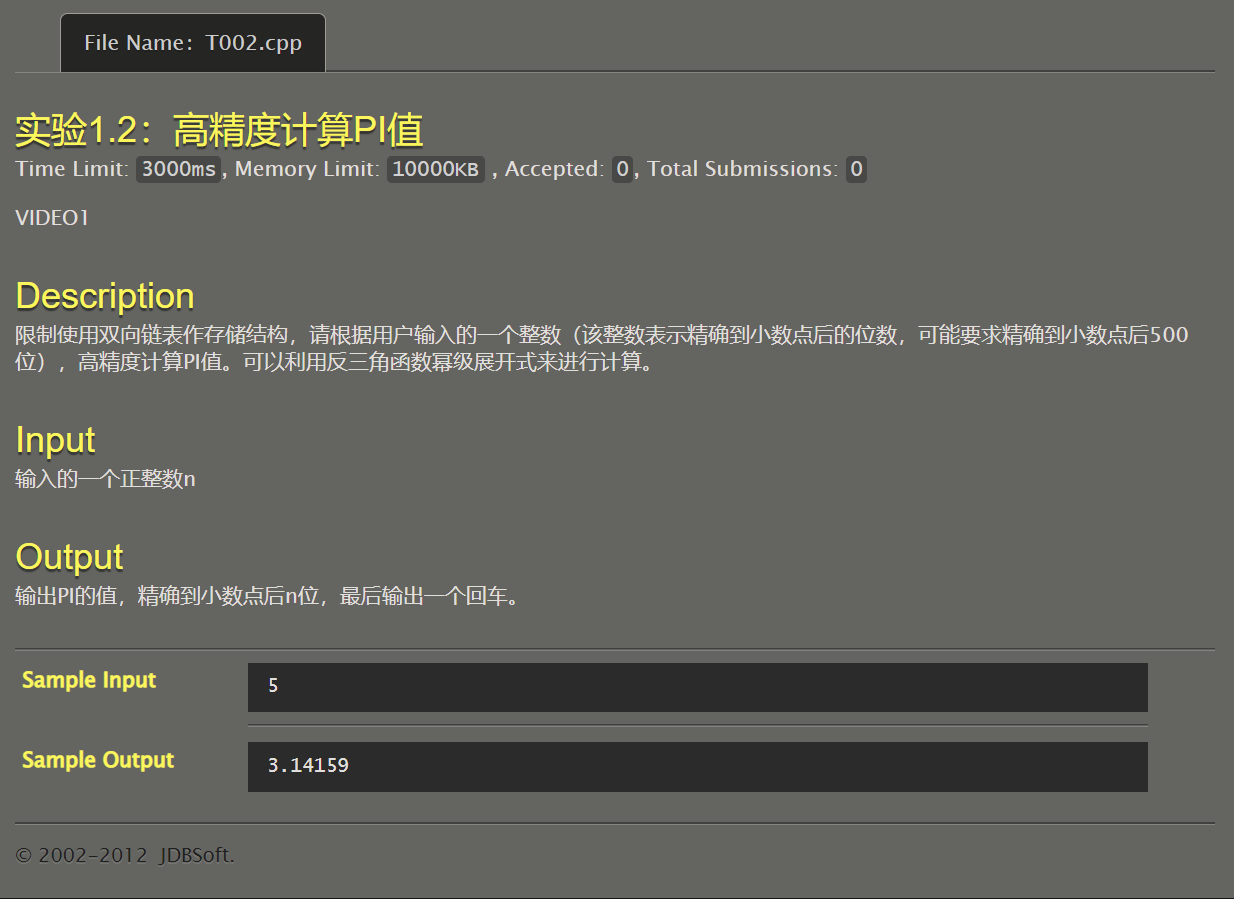
这次我们的最低目标是在3000ms的限制内,实现计算 π π π 到小数点后500位。
?1.公式选择
首先,如果不清楚如何计算 π π π 的同学可以先参考下面的文章,有助于理解下面的公式选择。
π 是怎么算出来的?
相信大家看完后已经对 π π π 的求法有一定的认识了,所以这里给出几个关于 π π π 的几个公式:
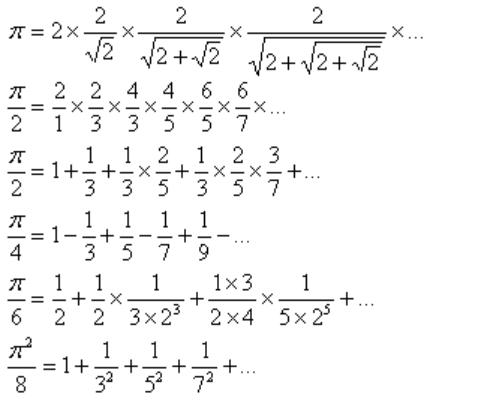
我们这里选择第三个公式,为什么呢?
当然是因为第三个公式是题目给出的反正切函数的幂次展开式啦(bushi)
其实是因为第三个公式是线性收敛,平均每计算一次就会得到0.3个有效数字,相比于第四个 a r c t a n x arctanx arctanx泰勒展开公式(莱布尼茨公式)来说,效率上会高出很多,而且最重要的一点是它比较容易实现,递推公式如下:
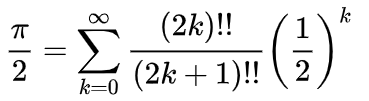
将其展开就是第三个公式,大家可以对比着看。
关于 a r c t a n x arctanx arctanx泰勒展开计算 π π π 可以参考此篇文章:π的计算
反正切函数的幂次展开式的推导具体过程:
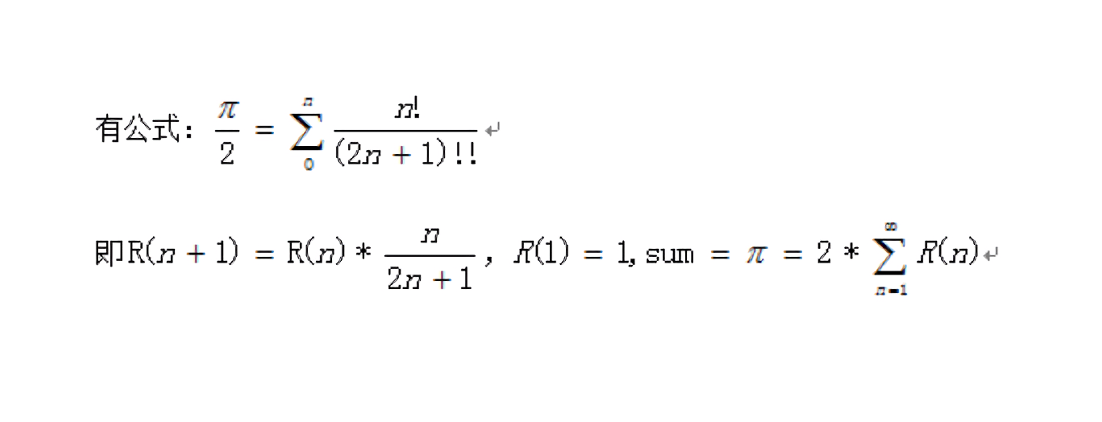
?2.实现难点解析
关于大数实现:
这里我们选择 C++ 模板中的 list 类来实现(也可以使用string类等,只要可以进行大数四则运算就可以,这里为了符合题意使用链表),由于 π π π 的整数部分为3,所以我们只需要一位来存储整数部分,也即front存储整数部分,其余小数点以后的位顺次向后连接。
我们的核心目标是要实现:
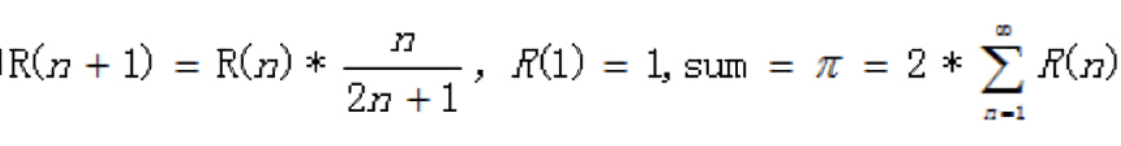
我们将上面的任务拆开,分解成一个个独立的任务
R ( n ) ∗ n R(n) * n R(n)∗n这里我们选择模拟竖式乘法:
从链表尾结点开始,每个结点的数乘n。结点中只能存放个位数,所以当乘得结果大于等于10,需要保存进位。每次计算乘法时,还需要加上前一个数的进位。循环上述过程,直到头节点。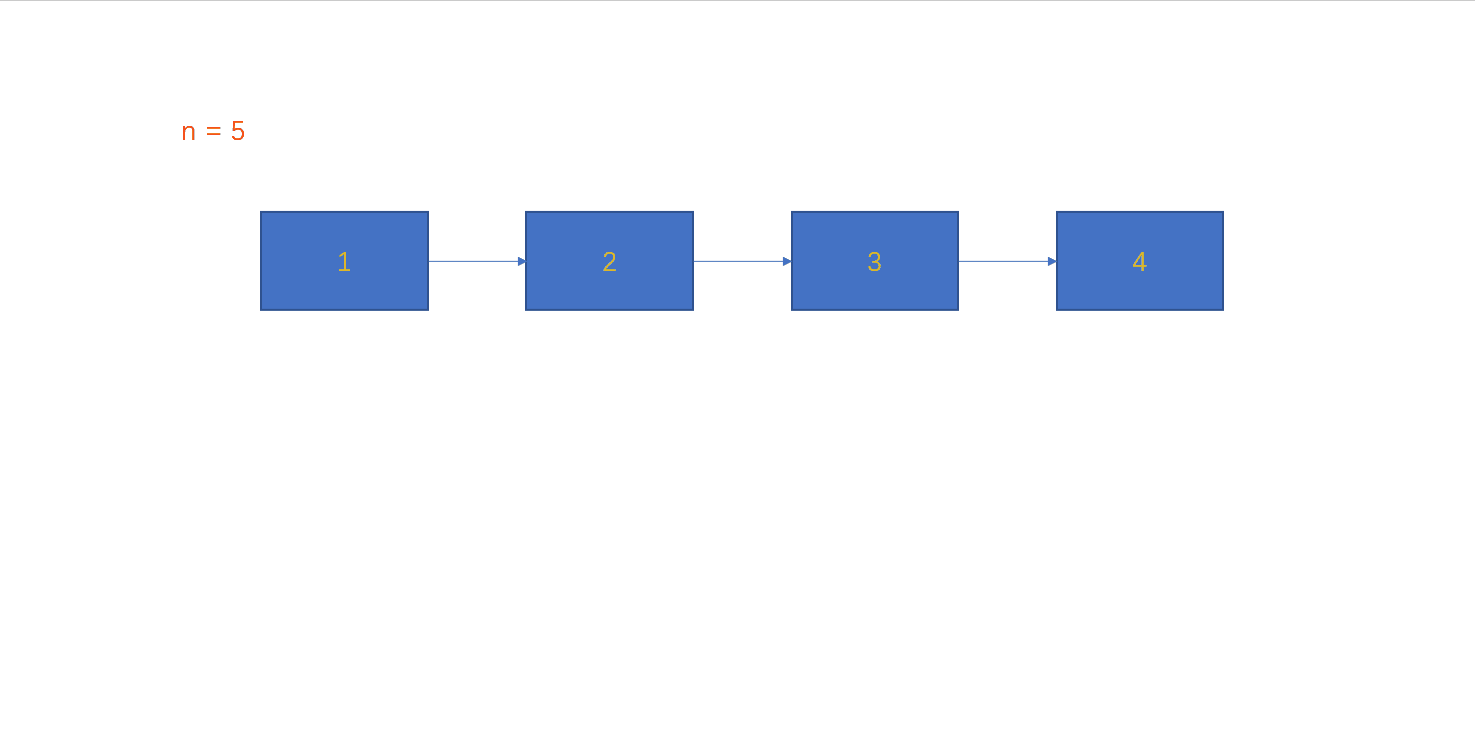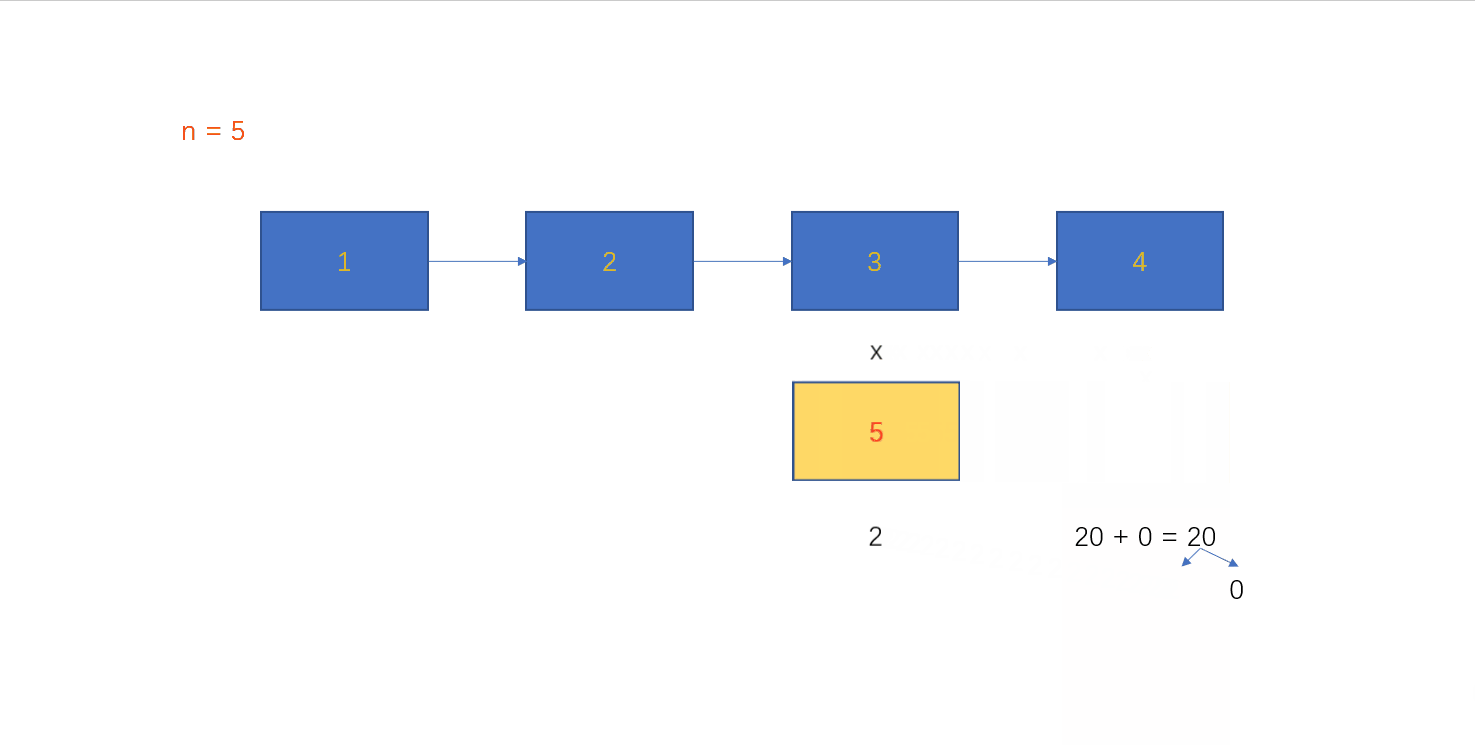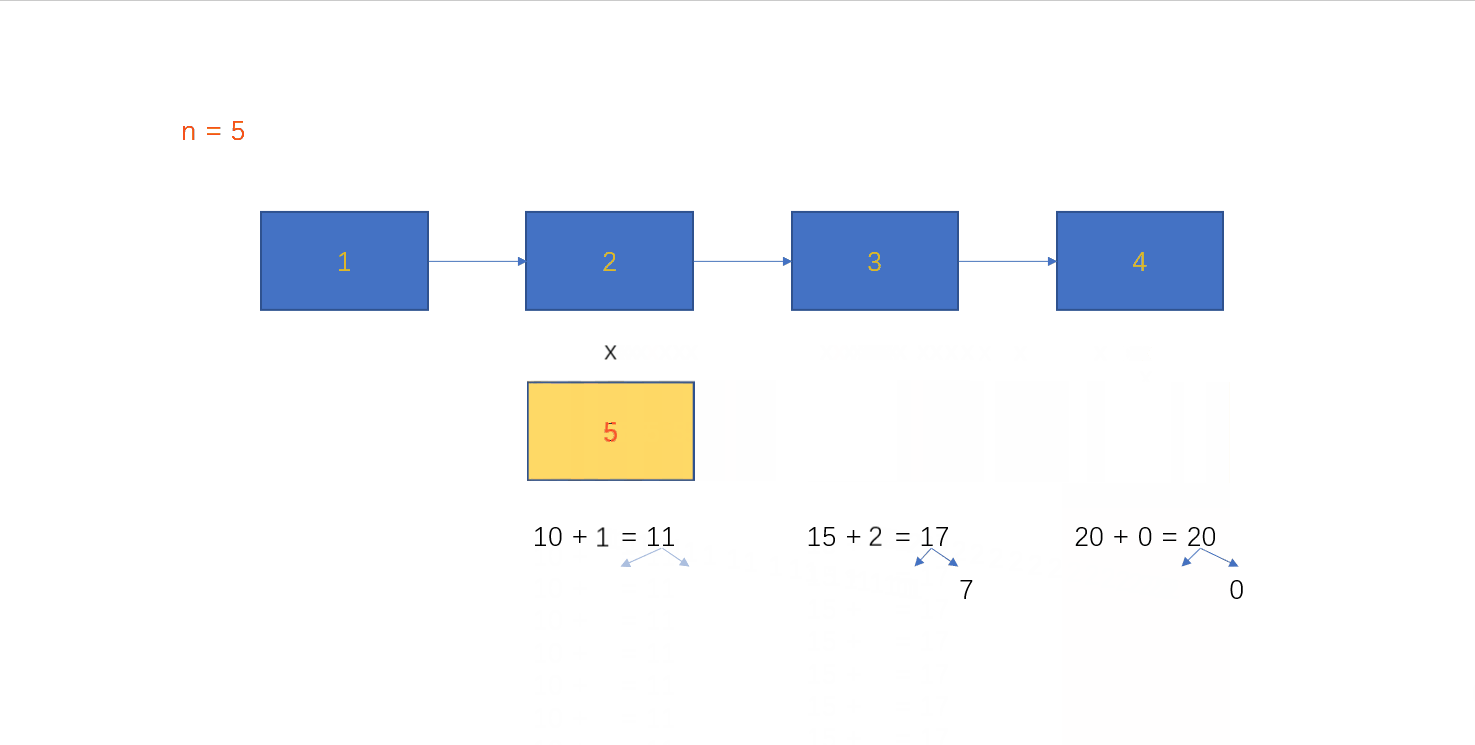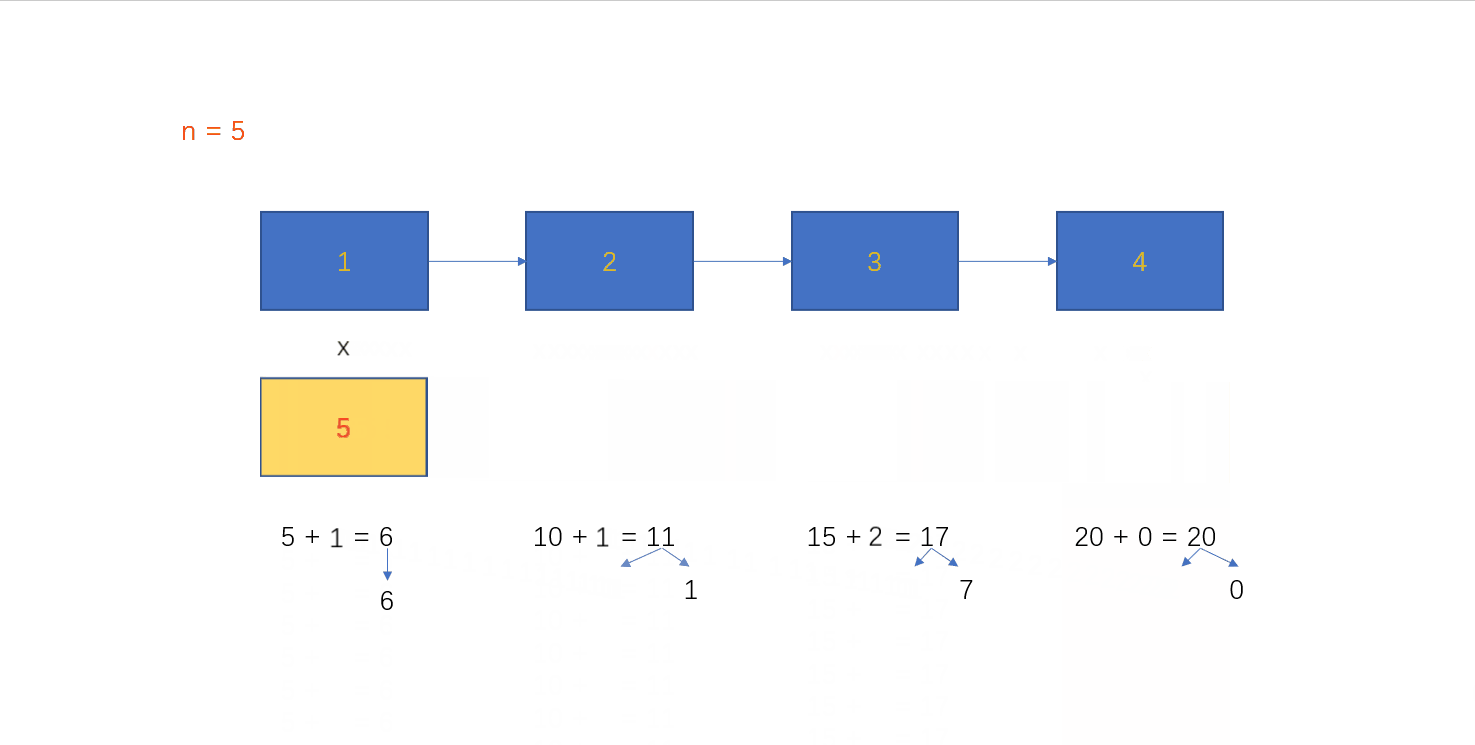
这里我们选择模拟竖式除法:
用上面乘法得到的结果除以(2n + 1)。除法与乘法相反,我们要从头节点开始除法。每一位除以(2n + 1)得到的结果就是:(此节点的值 + 上一个结点的余数*10) /(2n + 1)。再保存这个结点除以(2n + 1)后所得的余数。循环上述过程,直到尾节点此处不再演示,大家可以类比乘法动手模拟一下,其实非常相似,代码也很相似。
S u m ( n + 1 ) = S u m ( n ) + R ( n + 1 ) Sum(n + 1) = Sum(n) + R(n + 1) Sum(n+1)=Sum(n)+R(n+1)这就是递推公式的最后一步,将上面计算得到的 R ( n + 1 ) R(n+1) R(n+1) 加到 S u m ( n ) Sum(n) Sum(n) 上,这其实就是一个大数加法的问题,我们选择模拟竖式加法:
从最低位开始, R ( n + 1 ) R(n+1) R(n+1) 与 S u m ( n ) Sum(n) Sum(n) 对应的位相加。相加得到的值如果大于等于10,需要进位。对应位相加得到的结果需要加上进位循环上述过程,直到头节点此过程与乘法非常相近,在后面的代码实现中我们可以看出。
关于链表结点个数链表结点数代表着小数点后的位数,所以当然是结点越多越精确,但是结点数太多会影响性能。如果我们要实现500位的精确值,我的建议是创建550~600个结点即可。
关于要迭代的次数这里有两种根据所求精度估算大致的迭代的次数的方法:
估算精度
int count(int n) {int i = 1;double sum = 0;int a, b;while(1){a = 2 * i + 1;b = i;sum = sum + log10(a / b);i++;if (sum > n + 1) {return i;}}}参考文章:数据结构实验1.2—高精度计算PI值(西工大)
估算有效数字

int count(int n){double ret = (double)n;return (int)(ret / 0.3);}参考文章:目前求 π 的算法中哪种收敛最快?
以上两种方法都可以使用,根据我在release发布版本的测试下,两种方法没有数量级的差别,所以使用哪一种都可以。
注:如果要提升精度,必须也增大结点个数,不能只增加迭代次数
测试结果:
方法一: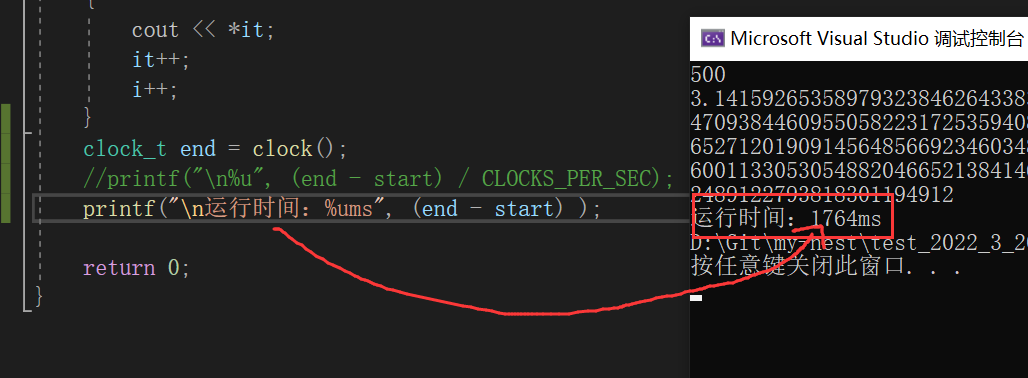
方法二: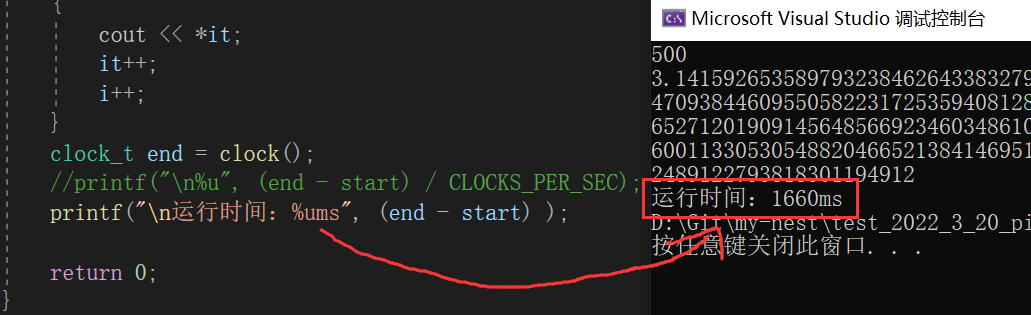
?3.代码实现
#include <time.h>#include <iostream>#include <list>#include<math.h>using namespace std;// 估测要计算的次数// 方法一:int count(int n) {int i = 1;double sum = 0;int a, b;while(1){a = 2 * i + 1;b = i;sum = sum + log10(a / b);i++;if (sum > n + 1) {return i;}}}// 方法二:int count(int n){double ret = (double)n;return (int)(ret / 0.3);}int main(){// 定义我们需要多少个结点#define NODE_NUM 550list<int> num(NODE_NUM, 0);// 存放R(n)list<int> sum(NODE_NUM, 0);// 存放Sum(n)int print;// 所需精度cin >> print;int cnt = count(print);// 所需迭代次数 // 我们直接将 R(1) 初始化为2,这样就可以免去后面再统一乘2num.front() = 2;sum.front() = 2;// 这里循环的 i 就是 n for (int i = 1; i <= cnt; ++i){int ret = 0;// 记录进位,补位情况 // 计算R(n + 1)// 计算 R(n) * nfor (list<int>::reverse_iterator cur1 = num.rbegin(); cur1 != num.rend(); cur1++){ // 每一位都是本位乘i,再加上进位int val = *cur1 * i + ret; // 保存进位ret = val / 10; // 保存本位*cur1 = val % 10;}ret = 0;// 计算 R(n) * n / (2n + 1)for (list<int>::iterator cur1 = num.begin(); cur1 != num.end(); cur1++){ // 除数int div = (i << 1) + 1; // 加上前一位的余数int val = *cur1 + ret * 10; // 除法,保存本位*cur1 = val / div; // 保存余数ret = val - *cur1 * div;}ret = 0;// 计算 sum += R(n + 1)for (auto cur2 = sum.rbegin(), cur1 = num.rbegin(); cur2 != sum.rend(); cur2++, cur1++){ // 大数加法int val = *cur1 + *cur2 + ret;*cur2 = val % 10;ret = val / 10;}}// 打印cout << sum.front() << '.';list<int>::iterator it = sum.begin();it++;int i = 0;while (i < print){cout << *it;it++;i++;}return 0;}?后记
这个方法其实还是有改进的细节,比如:
将输入输出更换为scanf和printf,因为其实在效率上 cin和cout 比前者慢了几十倍,在输出大型数字时,效率会受影响。公式限制,其实比反正切幂次展开更高效的公式还是很多,这里只是为了实现简单和逻辑清晰而选择了反正切幂次展开,大家有兴趣可以参考下图公式自己去实现。
参考文章:目前求 π 的算法中哪种收敛最快?
这是一个新的系列 ——【算法】,想来想去将这个计算 π π π 的文章放到了【算法】系列的开篇。因为其中确实有不少算法的实现,并且难度不是很大,很适合想学习C++或者算法的入门学习,在探求 π π π 的实践中一路学习高数?和编程(bushi)。
如果解析有不对之处还请指正,我会尽快修改,多谢大家的包容。
如果大家喜欢这个系列,还请大家多多支持啦?!
如果这篇文章有帮到你,还请给我一个大拇指 ?和小星星 ⭐️支持一下白晨吧!喜欢白晨【算法】系列的话,不如关注?白晨,以便看到最新更新哟!!!
我是不太能熬夜的白晨,我们下篇文章见。