目录
前言NSGA-II非支配排序支配关系非支配关系非支配排序算法算法思想算法伪代码伪代码释义Python代码实现 过渡1拥挤度距离排序算法思想算法伪代码Python代码实现 过渡2二元锦标赛 精英选择策略选择交叉变异生成新种群选择交叉变异Python代码实现 整体流程图测试函数与结果 其他
前言
由于NSGA-II是基于遗传算法的,所以在讲解NSGA-II之前,我们先对遗传算法有一些基本的了解——遗传算法经常用于单目标优化问题,所进行操作的基本流程如下
通过解的二进制值进行交叉变异产生不同的解依据适应度函数,得到每个解的适应值根据适应值的大小来对当前解集合,进行排序筛选。再对筛选出的个体进行新一轮的交叉变异,循环往复使得解集合越来越逼近真实的优化目标。 NSGA-II所做的其实就是把排序的依据改变——就是“如何评判一个解的优劣”,在传统遗传算法中,使用的是适应度函数值,这也是因为传统遗传算法多用在单目标的优化问题中,使用能够使用这一个指标来判断。
下面是遗传算法中一些名词的对应关系:
| 数学概念 | 生物概念 |
|---|---|
| 当前的解集合 | 当前的种群 |
| 解集合中的每个解 | 种群中的个体 |
NSGA-II
但对于一个多目标优化问题来说,它的最优解不再是一个值,而是在多维空间中的一个pareto前沿:一个最优解的集合。因此对于迭代过程中未到达pareto前沿的解来说,评判其优劣应当从两个方面来入手——
收敛性——解靠近pareto前沿的程度(或速度)
分布性——当前解集是否尽可能地覆盖到了pareto前沿。
所以NSGA-II的作者Deb提出了评价当前解集合优劣的两个指标:
下面为了方便讲解,我们以双目标的最小化优化问题举例说明,因为这样能够在几何意义上,放在二维平面图中帮助我们去理解。
m i n F ( x ) = { f 1 ( x ) , f 2 ( x ) } T s t . x ∈ X X ⊂ R 2 min \quad F(x)=\{f_1(x),f_2(x)\}^T\\ st. \quad x\in X \\ \quad \quad X \subset\mathbb R^2 minF(x)={f1(x),f2(x)}Tst.x∈XX⊂R2
非支配排序
支配关系
首先,需要了解两个解的支配关系。我们举例来说明,如果两个目标都是最小化目标的话,说明目标函数值越小,越好。则假设
给定个体 x 0 x_0 x0,
目标函数值 F ( x 0 ) = ( f 1 ( x 0 ) , f 2 ( x 0 ) ) = ( 1 , 1 ) F(x_0) =(f_1(x_0),f_2(x_0))=(1,1) F(x0)=(f1(x0),f2(x0))=(1,1)
再给定另外的个体 x 1 x_1 x1,
目标函数值 F ( x 1 ) = ( f 1 ( x 1 ) , f 2 ( x 1 ) ) = ( 2 , 2 ) F(x_1) =(f_1(x_1),f_2(x_1))=(2,2) F(x1)=(f1(x1),f2(x1))=(2,2)
我们可以发现, 在两个目标函数方向(objective), x 0 x_0 x0 所求的目标函数值 ( 1 , 1 ) (1,1) (1,1) 都比 x 1 x_1 x1 的目标函数值 ( 2 , 2 ) (2,2) (2,2) 小,而同时两个优化方向都是最小化。所以 x 0 x_0 x0 所得解的效果要要好于 x 1 x_1 x1 ,即 x 0 x_0 x0 支配 x 1 x_1 x1。
同样的,当一个方向上相等,支配关系又另一个方向目标函数值的大小来决定,例如: ( 1 , 2 ) (1,2) (1,2) 支配 ( 2 , 2 ) (2,2) (2,2)。
如果在二维平面图上用几何意义来理解的话,就是由原点开始向外做同心圆,内侧圆上的点支配外侧圆上的点。(当然仅限于两个目标,且优化方向都是最小化)
非支配关系
但是我们会遇到另外一种情况,例如 ( 1 , 2 ) (1,2) (1,2) 和 ( 2 , 1 ) (2,1) (2,1) ,显然在一个方向上2 > 1,但在另一个方向上1 < 2,对应在几何意义上,就是这两个点在同一个圆上。像这种彼此没有明确的支配关系,即双方无法支配对方的时候,两者的关系就是非支配关系。
综上对于两个个体而言,他们的大小关系便可以对应为两者的支配关系。所以在类定义中,我重载了小于号的方法,方便在代码中比较两个个体的支配关系。
# 重载小于号“<” def __lt__(self, other): v1 = list(self.objective.values()) v2 = list(other.objective.values()) for i in range(len(v1)): if v1[i] > v2[i]: return 0 # 但凡有一个位置是 v1大于v2的 直接返回0,如果相等的话比较下一个目标值 return 1非支配排序算法
算法思想
由上,显然支配关系能够作为一个指标来衡量这个解的优劣程度,因此我们利用个体间的支配关系,将现有种群进行分层。最靠近pareto前沿的解它的等级(rank)最高,为第一层。然后依次判断每个个体处在第几层中,给每个个体的rank赋值。几何上来看,类似于画同心圆,看看这个解在第几个同心圆中。然后依据每个个体的rank值来进排序选择。
算法伪代码
下面是原文作者的伪代码:
伪代码释义
这里面需要了解其中几个变量的含义——
n p n_p np:解 p p p 被几个解所支配,是一个数值(左下部分点的个数)
S p S_p Sp:解 p p p 支配哪些解,是一个解集合(右上部分点的内容)
F i F_i Fi:第 i i i 层的解集合(显然同一层内的解互相都是非支配解)
p r a n k p_{rank} prank:解 p p p 所在层的等级(越小越好)
伪代码主要进行了两步:
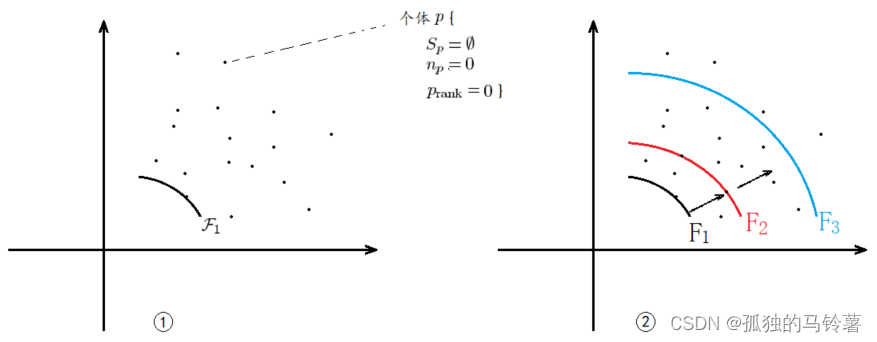
Python代码实现
def fast_non_dominated_sort(P): """ 非支配排序 :param P: 种群 P :return F: F=(F_1, F_2, ...) 将种群 P 分为了不同的层, 返回值类型是dict,键为层号,值为 List 类型,存放着该层的个体 """ F = defaultdict(list) for p in P: p.S = [] p.n = 0 for q in P: if p < q: # if p dominate q p.S.append(q) # Add q to the set of solutions dominated by p elif q < p: p.n += 1 # Increment the domination counter of p if p.n == 0: p.rank = 1 F[1].append(p) i = 1 while F[i]: Q = [] for p in F[i]: for q in p.S: q.n = q.n - 1 if q.n == 0: q.rank = i + 1 Q.append(q) i = i + 1 F[i] = Q return F过渡1
上面描述的非支配排序方法从解的收敛性,或者说靠近pareto的前沿的程度来衡量解的优劣。以此,我们假设现在待选择种群个体有120个,我们的种群规模为100,即要选择前100个作为父代进入下一次迭代。
通过非支配排序,若得到 F 1 F_1 F1 有30个, F 2 F_2 F2 有60个, F 3 F_3 F3 有10个, F 4 F_4 F4 有20个。很显然,我们只选择 F 1 F_1 F1 , F 2 F_2 F2 , F 3 F_3 F3 中的个体就可以了。但上述情况是刚刚好的,我们需要考虑比较一般的情况——
如果划分的线切在了 F i F_i Fi 层中,即如果 F 3 F_3 F3 有30个,要从中选择10个,剔除20个,这种情况该如何选择呢?即对于处在同一层中,rank属性值相同的个体,我们应当依据什么来对他们进行排序呢?
拥挤度距离排序
算法思想
由此,作者为了保证种群的多样性,即保留解的分布的稀疏程度,放在图上来看的话就是尽可能得让解分散。在这一原则之下,位于两端的解是必留的,而处于中间的点,则通过定义拥挤度距离来进行判断。形象一些来理解的话,就是“你身边距离比较近的同类太多了,只留下你一个能够代表这一段就行了”。
算法伪代码
下面是原文作者的伪代码: 该段代码比较简单,在不同目标方向上,对于两端点(目标值最大和最小的)的拥挤度距离直接设置为正无穷,而对于中间的点遵循一个公式,简单概括为:
该段代码比较简单,在不同目标方向上,对于两端点(目标值最大和最小的)的拥挤度距离直接设置为正无穷,而对于中间的点遵循一个公式,简单概括为:
Python代码实现
def crowding_distance_assignment(L): """ 传进来的参数应该是L = F(i),类型是List""" l = len(L) # number of solution in F for i in range(l): L[i].distance = 0 # initialize distance for m in L[0].objective.keys(): L.sort(key=lambda x: x.objective[m]) # sort using each objective value L[0].distance = float('inf') L[l - 1].distance = float('inf') # so that boundary points are always selected # 排序是由小到大的,所以最大值和最小值分别是 L[l-1] 和 L[0] f_max = L[l - 1].objective[m] f_min = L[0].objective[m] for i in range(1, l - 1): # for all other points L[i].distance = L[i].distance + (L[i + 1].objective[m] - L[i - 1].objective[m]) / (f_max - f_min) # 虽然发生概率较小,但为了防止除0错,当bug发生时请替换为以下代码 # if f_max != f_min: # for i in range(1, l - 1): # for all other points # L[i].distance = L[i].distance + (L[i + 1].objective[m] - L[i - 1].objective[m]) / (f_max - f_min)过渡2
由此介绍完“非支配排序”和“拥挤度距离分配”之后,对于一个已有种群的排序选择的基本流程便可以确定下来——
给定种群中的两个个体,首先比较其rank,该值越小,说明其越靠近pareto前沿,故选择rank值小的。若两个个体的rank值相同,即两个解是非支配解时,比较其crowding_distance,该值越大,表示其所处的位置更稀疏,更能表现出种群的多样性,故选择crowding_distance值大的。二元锦标赛
以上流程便是 “二元锦标赛”选择的基本策略。(二元锦标赛:随机选择两个个体,依据某种指标策略进行比较,较优的个体胜出,作为进行交叉的父本中的一个)
其对应代码如下
def binary_tournament(ind1, ind2): """ 二元锦标赛 :param ind1:个体1号 :param ind2: 个体2号 :return:返回较优的个体 """ if ind1.rank != ind2.rank: # 如果两个个体有支配关系,即在两个不同的rank中,选择rank小的 return ind1 if ind1.rank < ind2.rank else ind2 elif ind1.distance != ind2.distance: # 如果两个个体rank相同,比较拥挤度距离,选择拥挤读距离大的 return ind1 if ind1.distance > ind2.distance else ind2 else: # 如果rank和拥挤度都相同,返回任意一个都可以 return ind1精英选择策略
首先,在传统的遗传算法中,在某一次迭代中,只有该次迭代的父代参与选择交叉变异,从而产生子代,作为下一次迭代的父代。
而在NSGA-II中,为了保证最优解的不丢失,提高算法的收敛速度,作者提出了“精英选择策略”,即将父代 P t P_t Pt 和子代 Q t Q_t Qt 种群,合并为一个种群 R t R_t Rt ,对其整体进行非支配排序和拥挤度距离计算,根据上述方法进行排序和选择作为下一届的父代 P t + 1 P_{t+1} Pt+1 。父代再通过一般的方法进行选择交叉排序产生子代 Q t + 1 Q_{t+1} Qt+1 。
这里同样也是循环的主流程所在!

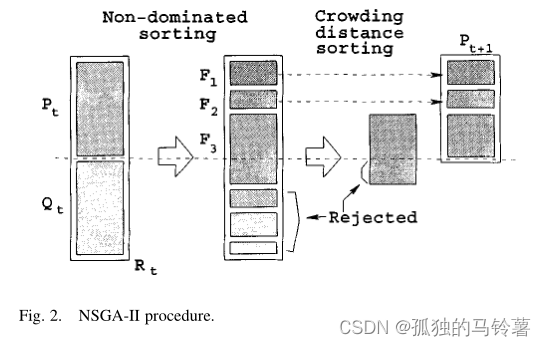
选择交叉变异生成新种群
选择
随机从种群中选择两个个体,让其进行过渡2所说的“二元锦标赛”,获胜的作为父本1;同样操作,再得到一个父本2。之后,为了避免遗传算法中的早熟现象,多增加一步判断,使得父本1和父本2不相同。
交叉
对得到的两个父本进行交叉,产生两个子代。这里选择的交叉算子是“模拟二进制交叉(SBX)”
变异
对于得到的两个子代,其中一个进行变异操作,另一个不变(千万不要两个都变,会引起一种早熟现象——所有的个体都过早的陷于某几个极值而停止变化,具体原因未明,待解决),这里选择的变异算子是“多项式变异”(PM)
x j = x j + Δ j Δ j = { ( 2 μ i ) 1 η + 1 μ i < 0.5 1 − [ 2 ( 1 − μ i ) ] 1 η + 1 μ i ≥ 0.5 x_j=x_j+ \Delta_j \\ ~\\ ~\\ \Delta_j = \begin{cases} (2\mu_i)^{\frac{1}{\eta + 1}} & \mu_i<0.5 \\ 1-[2(1-\mu_i)]^{\frac{1}{\eta + 1}} & \mu_i\ge0.5 \end{cases} xj=xj+Δj Δj={(2μi)η+111−[2(1−μi)]η+11μi<0.5μi≥0.5
μ i \mu_i μi 是满足(0,1)均匀分布的随机数, η \eta η 是变异分布参数。
Python代码实现
def make_new_pop(P, eta, bound_min, bound_max, objective_fun): """ use select,crossover and mutation to create a new population Q :param P: 父代种群 :param eta: 变异分布参数,该值越大则产生的后代个体逼近父代的概率越大。Deb建议设为 1 :param bound_min: 定义域下限 :param bound_max: 定义域上限 :param objective_fun: 目标函数 :return Q : 子代种群 """ popnum = len(P) Q = [] # binary tournament selection for i in range(int(popnum / 2)): # 从种群中随机选择两个个体,进行二元锦标赛,选择出一个 parent1 i = random.randint(0, popnum - 1) j = random.randint(0, popnum - 1) parent1 = binary_tournament(P[i], P[j]) # 从种群中随机选择两个个体,进行二元锦标赛,选择出一个 parent2 i = random.randint(0, popnum - 1) j = random.randint(0, popnum - 1) parent2 = binary_tournament(P[i], P[j]) while (parent1.solution == parent2.solution).all(): # 如果选择到的两个父代完全一样,则重选另一个 i = random.randint(0, popnum - 1) j = random.randint(0, popnum - 1) parent2 = binary_tournament(P[i], P[j]) # parent1 和 parent1 进行交叉,变异 产生 2 个子代 Two_offspring = crossover_mutation(parent1, parent2, eta, bound_min, bound_max, objective_fun) # 产生的子代进入子代种群 Q.append(Two_offspring[0]) Q.append(Two_offspring[1]) return Qdef crossover_mutation(parent1, parent2, eta, bound_min, bound_max, objective_fun): """ 交叉方式使用二进制交叉算子(SBX),变异方式采用多项式变异(PM) :param parent1: 父代1 :param parent2: 父代2 :param eta: 变异分布参数,该值越大则产生的后代个体逼近父代的概率越大。Deb建议设为 1 :param bound_min: 定义域下限 :param bound_max: 定义域上限 :param objective_fun: 目标函数 :return: 2 个子代 """ poplength = len(parent1.solution) offspring1 = Individual() offspring2 = Individual() offspring1.solution = np.empty(poplength) offspring2.solution = np.empty(poplength) # 二进制交叉 for i in range(poplength): rand = random.random() beta = (rand * 2) ** (1 / (eta + 1)) if rand < 0.5 else (1 / (2 * (1 - rand))) ** (1.0 / (eta + 1)) offspring1.solution[i] = 0.5 * ((1 + beta) * parent1.solution[i] + (1 - beta) * parent2.solution[i]) offspring2.solution[i] = 0.5 * ((1 - beta) * parent1.solution[i] + (1 + beta) * parent2.solution[i]) # 多项式变异 # TODO 变异的时候只变异一个,不要两个都变,不然要么出现早熟现象,要么收敛速度巨慢 why? for i in range(poplength): mu = random.random() delta = (2 * mu) ** (1 / (eta + 1)) if mu < 0.5 else (1 - (2 * (1 - mu)) ** (1 / (eta + 1))) offspring1.solution[i] = offspring1.solution[i] + delta # 定义域越界处理 offspring1.bound_process(bound_min, bound_max) offspring2.bound_process(bound_min, bound_max) # 计算目标函数值 offspring1.calculate_objective(objective_fun) offspring2.calculate_objective(objective_fun) return [offspring1, offspring2]整体流程图
以上,便是所有需要的零件了,下面就是写主函数了,写程序嘛,还是得看具体的流程图: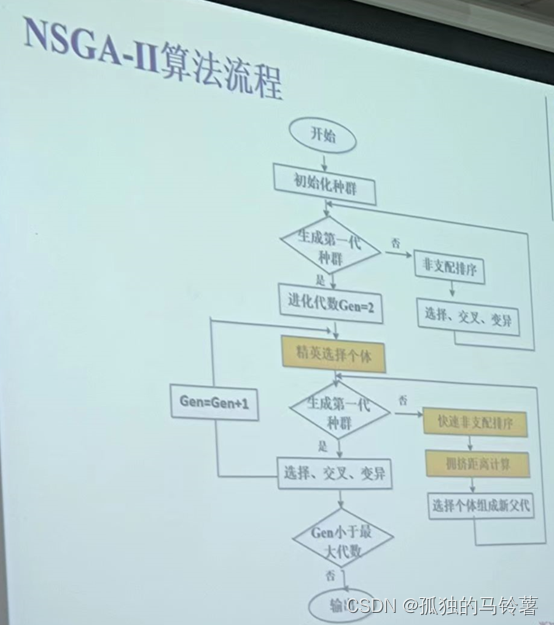
由此,主函数部分的Python代码实现如下:
def main(): # 初始化/参数设置 generations = 250 # 迭代次数 popnum = 100 # 种群大小 eta = 1 # 变异分布参数,该值越大则产生的后代个体逼近父代的概率越大。Deb建议设为 1 poplength = 30 # 单个个体解向量的维数 bound_min = 0 # 定义域 bound_max = 1 objective_fun = ZDT2 # poplength = 3 # 单个个体解向量的维数 # bound_min = -5 # 定义域 # bound_max = 5 # objective_fun = KUR # 生成第一代种群 P = [] for i in range(popnum): P.append(Individual()) P[i].solution = np.random.rand(poplength) * (bound_max - bound_min) + bound_min # 随机生成个体可行解 P[i].bound_process(bound_min, bound_max) # 定义域越界处理 P[i].calculate_objective(objective_fun) # 计算目标函数值 # 否 -> 非支配排序 fast_non_dominated_sort(P) Q = make_new_pop(P, eta, bound_min, bound_max, objective_fun) P_t = P # 当前这一届的父代种群 Q_t = Q # 当前这一届的子代种群 for gen_cur in range(generations): R_t = P_t + Q_t # combine parent and offspring population F = fast_non_dominated_sort(R_t) P_n = [] # 即为P_t+1,表示下一届的父代 i = 1 while len(P_n) + len(F[i]) < popnum: # until the parent population is filled crowding_distance_assignment(F[i]) # calculate crowding-distance in F_i P_n = P_n + F[i] # include ith non dominated front in the parent pop i = i + 1 # check the next front for inclusion F[i].sort(key=lambda x: x.distance) # sort in descending order using <n,因为本身就在同一层,所以相当于直接比拥挤距离 P_n = P_n + F[i][:popnum - len(P_n)] Q_n = make_new_pop(P_n, eta, bound_min, bound_max, objective_fun) # use selection,crossover and mutation to create a new population Q_n # 求得下一届的父代和子代成为当前届的父代和子代,,进入下一次迭代 《=》 t = t + 1 P_t = P_n Q_t = Q_n # 绘图 plt.clf() plt.title('current generation:' + str(gen_cur + 1)) plot_P(P_t) plt.pause(0.1) plt.show() return 0测试函数与结果
在此,测试函数使用ZDT1(论文还给出了很多其他的测试函数,具体可以看原论文的TABLE1):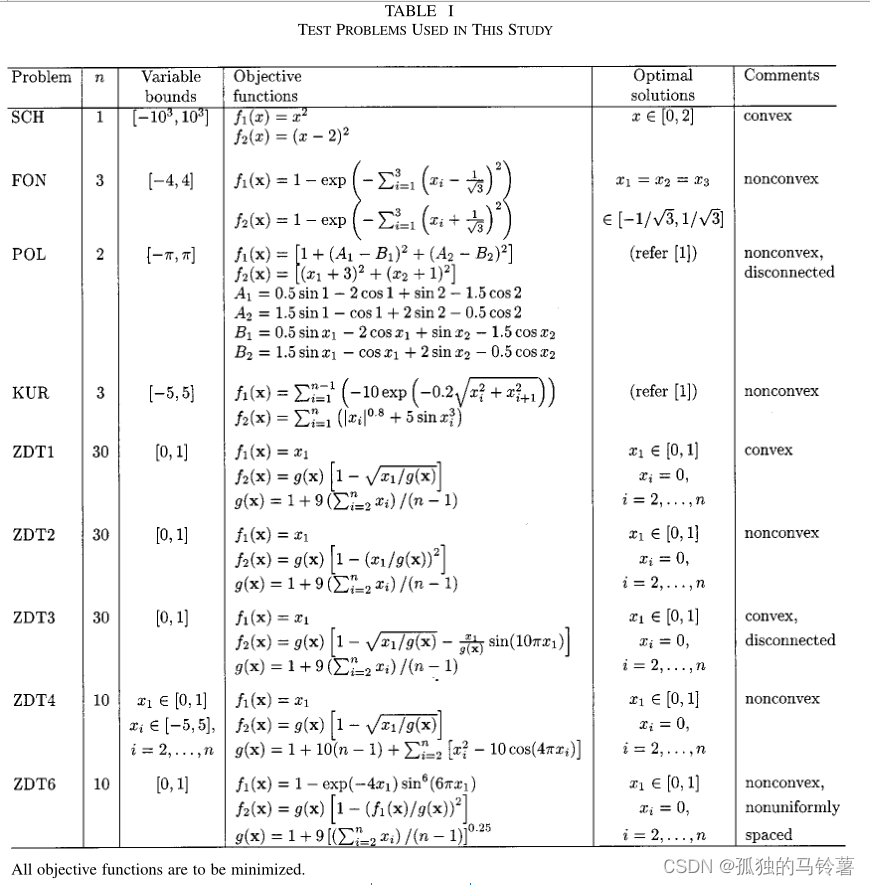
得到的结果如下: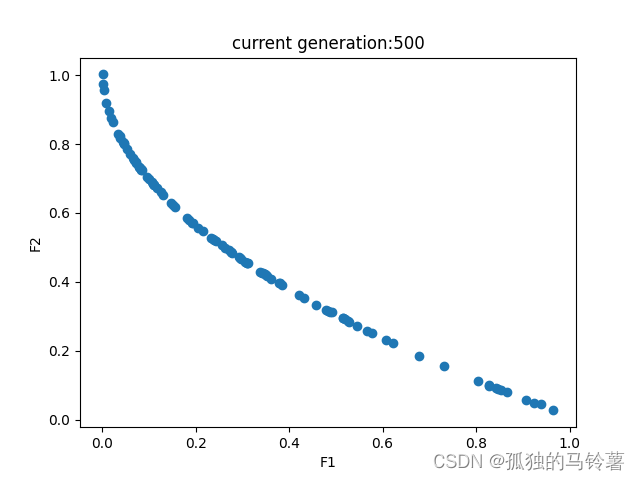
其他
源代码地址:
https://github.com/Jiangtao-Hao/NSGA-II.git
参考:
https://blog.csdn.net/Ryze666/article/details/123826212
https://www.docin.com/p-567112189.html