一、基本原理
图像边缘是图像的重要信息,而Canny算子则是用于边缘检测的经典算法。在用Canny算子进行边缘检测之前必须有效地抑制噪声,该算法使用的是高斯平滑滤波。接下来计算图像中每一点的梯度向量,根据梯度向量可以得到梯度方向和梯度幅值。梯度方向在(-π,π]范围内,将梯度方向离散到4个方向,分别为上下方向、左右方向、主对角线方向、副对角线方向,根据离散后的梯度方向对梯度幅值进行非极大值抑制。例如,如果图像中点(x,y)的梯度方向沿上下方向,那么将点(x,y)的梯度幅值分别与点(x-1,y)和点(x+1,y)的梯度幅值进行比较;如果点(x,y)的梯度幅值大于另外两点,那么该点有可能是边缘点,将它的梯度幅值保留;如果点(x,y)的梯度幅值不大于另外两点,那么该点一定不是边缘点,将它的梯度幅值置零。接下来,用双阈值算法检测和连接边缘,高阈值用于检测边缘,低阈值用于连接边缘。在该算法中,取高阈值为梯度幅值最大值的0.3倍,取低阈值为梯度幅值最大值的0.1倍。如果某点的梯度幅值大于高阈值,那么该点一定是边缘点;如果某点的梯度幅值小于低阈值,那么该点一定不是边缘点;如果某点的梯度幅值介于低阈值和高阈值之间,那么该点有可能是边缘点,进一步,如果该点的8邻域的梯度幅值的最大值大于高阈值,那么将该点判定为边缘点。
二、实现步骤
(1)调用自定义函数myGauss生成高斯模板,高斯模板的大小和标准差均可以改变;
(2)将原图像f(x,y)与高斯模板做卷积,得到用高斯滤波器平滑后的图像g(x,y);
(3)用2×2一阶有限差分近似式来计算图像中各点的梯度向量: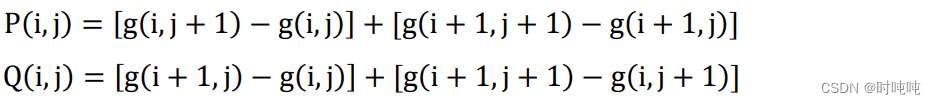
以上两个公式对应的模板分别如下;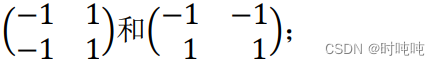
(4)利用梯度向量计算各点的梯度方向和梯度幅值: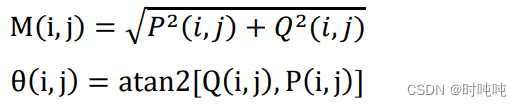
(5)将梯度方向离散到4个方向,即上下方向、左右方向、主对角线方向和副对角线方向;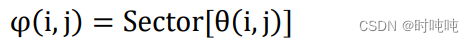
(6)根据离散后的梯度方向对梯度幅值进行非极大值抑制。例如,如果图像中点(x,y)的梯度方向沿上下方向,那么将点(x,y)的梯度幅值分别与点(x-1,y)和点(x+1,y)的梯度幅值进行比较;如果点(x,y)的梯度幅值大于另外两点,那么该点有可能是边缘点,将它的梯度幅值保留;如果点(x,y)的梯度幅值不大于另外两点,那么该点一定不是边缘点,将它的梯度幅值置零。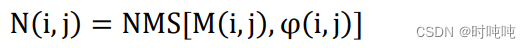
(7)用双阈值算法检测和连接边缘。高阈值和低阈值根据梯度幅值的最大值来确定,在该算法中,取: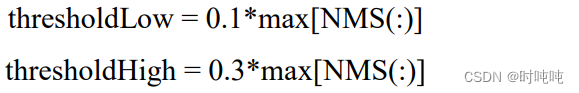
如果某点的梯度幅值大于高阈值,那么该点一定是边缘点;如果某点的梯度幅值小于低阈值,那么该点一定不是边缘点;如果某点的梯度幅值介于低阈值和高阈值之间,那么该点有可能是边缘点,进一步,如果该点的8邻域的梯度幅值的最大值大于高阈值,那么将该点判定为边缘点。
三、效果演示
(1)原始图像;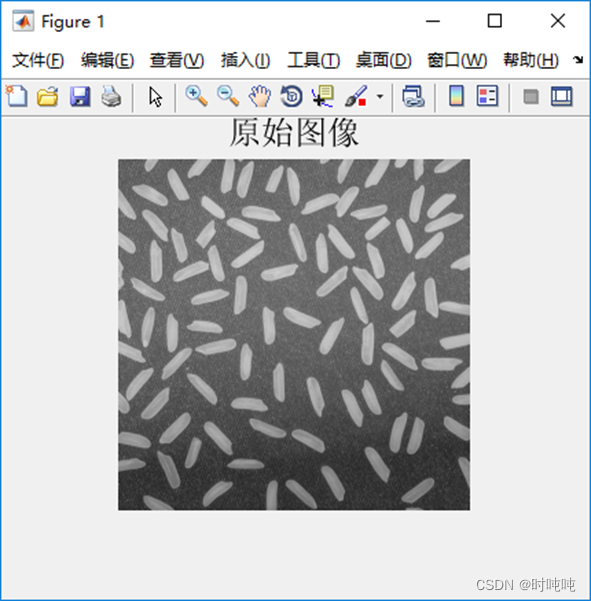
(2)高斯平滑后的图像;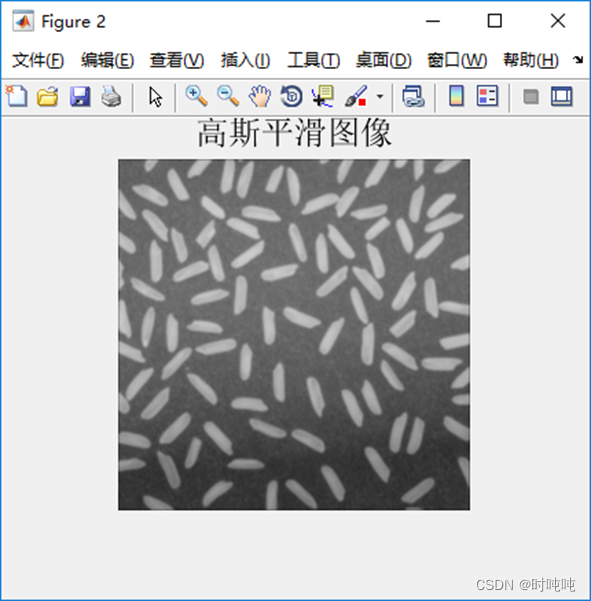
(3)Canny边缘检测的结果。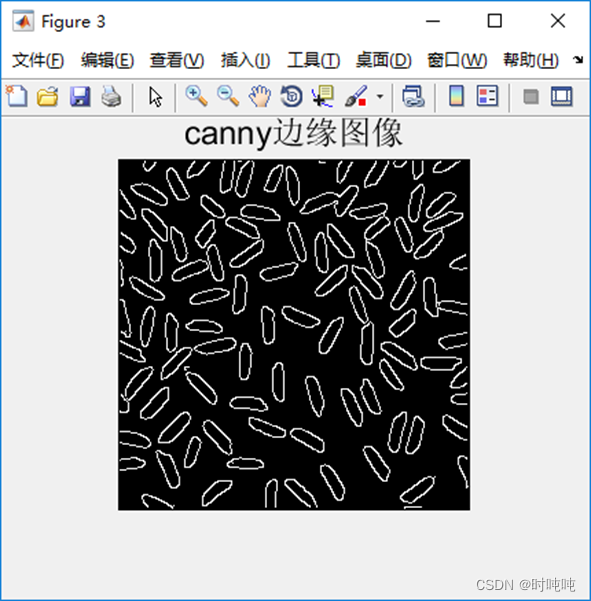
四、matlab实现代码
%% Canny边缘检测算子,高斯模板的大小和标准差均可以改变clear,close allclcsrcImg = imread('Canny算子用.png');figure;imshow(srcImg);title('原始图像','fontsize',18);srcImg = double(srcImg);[rows,cols] = size(srcImg);%% 用高斯滤波器平滑图像guassMask = myGauss(1,1,0.8);filteredImg = conv2(srcImg,guassMask,'same');figure;imshow(uint8(filteredImg));title('高斯平滑图像','fontsize',18);%% 计算梯度的幅值和方向maskX = [-1 -1; 1 1];maskY = [-1 1;-1 1];gradX = conv2(filteredImg,maskX,'same');gradY = conv2(filteredImg,maskY,'same');M = sqrt(gradX.^2+gradY.^2);theta = atan2(gradY,gradX);%% 对梯度幅值进行非极大值抑制(向下为X+,向右为Y+)for i = 1:rows for j = 1:cols if (theta(i,j)>=-pi/8 && theta(i,j)<pi/8)||(theta(i,j)>=pi*7/8 && theta(i,j)<=pi)||(theta(i,j)>-pi && theta(i,j)<-pi*7/8) theta(i,j) = 0; elseif (theta(i,j)>=pi/8 && theta(i,j)<pi*3/8)||(theta(i,j)>=-pi*7/8 && theta(i,j)<-pi*5/8) theta(i,j) = 45; elseif (theta(i,j)>=pi*3/8 && theta(i,j)<pi*5/8)||(theta(i,j)>=-pi*5/8 && theta(i,j)<-pi*3/8) theta(i,j) = 90; elseif (theta(i,j)>=pi*5/8 && theta(i,j)<pi*7/8)||(theta(i,j)>=-pi*3/8 && theta(i,j)<-pi/8) theta(i,j) = 135; end endendNMS = zeros(rows,cols);for i = 2:rows-1 for j = 2:cols-1 if theta(i,j)==0 && M(i,j)>M(i-1,j) && M(i,j)>M(i+1,j)% 比较中心像素点和上下两像素点的梯度幅值 NMS(i,j) = M(i,j); elseif theta(i,j)==45 && M(i,j)>M(i-1,j-1) && M(i,j)>M(i+1,j+1)% 比较中心像素点和主对角线两像素点的梯度幅值 NMS(i,j) = M(i,j); elseif theta(i,j)==90 && M(i,j)>M(i,j-1) && M(i,j)>M(i,j+1)% 比较中心像素点和左右两像素点的梯度幅值 NMS(i,j) = M(i,j); elseif theta(i,j)==135 && M(i,j)>M(i-1,j+1) && M(i,j)>M(i+1,j-1)% 比较中心像素点和副对角线两像素点的梯度幅值 NMS(i,j) = M(i,j); end endend%% 用双阈值算法检测和连接边缘dstImg = zeros(rows,cols);thresholdLow = 0.1*max(NMS(:));thresholdHigh = 0.3*max(NMS(:));for i = 2:rows-1 for j = 2:cols-1 if NMS(i,j) > thresholdHigh % 若某像素点的梯度幅值大于高阈值,则该像素点为边缘点 dstImg(i,j) = 1; elseif NMS(i,j)<thresholdLow % 若某像素点的梯度幅值小于低阈值,则该像素点非边缘点 dstImg(i,j) = 0; elseif max(max(NMS(i-1:i+1,j-1:j+1)))>thresholdHigh % 若某像素点的梯度幅值介于高阈值和低阈值之间,则检测该像素点的8邻域是否存在边缘像素点,如果存在,则该像素点为边缘点 dstImg(i,j) = 1; end endendfigure;imshow(dstImg);title('canny边缘图像','fontsize',18);%% 函数定义:产生高斯模板function gaussMask = myGauss(a,b,sigma) m = 2*a+1;% m为高斯模板的行数 n = 2*b+1;% n为高斯模板的列数 gaussMask = zeros(m,n); sigma2 = sigma*sigma;% sigma为标准差 for i = 1:m for j = 1:n gaussMask(i,j) = 1/(2*pi*sigma2)*exp(((i-a-1)*(i-a-1)+(j-b-1)*(j-b-1))/(-2*sigma2));% 计算高斯模板的系数 end end SUM = sum(gaussMask(:)); gaussMask = gaussMask/SUM;% 归一化end