数学建模层次分析法
1. 层次分析法的基本原理和步骤1.1 层次单排序及一致性检验1.2 层次总排序及一致性检验 2. matlab代码3. 应用过程举例4. 参考资料
1. 层次分析法的基本原理和步骤
层次分析法的基本原理与步骤
人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是
一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次
分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。

基本原理

运用层次分析法建模,大体上可按下面四个步骤进行:
(i) 建立递阶层次结构模型;(ii) 构造出各层次中的所有判断矩阵;(iii)层次单排序及一致性检验;(iv) 层次总排序及一致性检验。



1.1 层次单排序及一致性检验

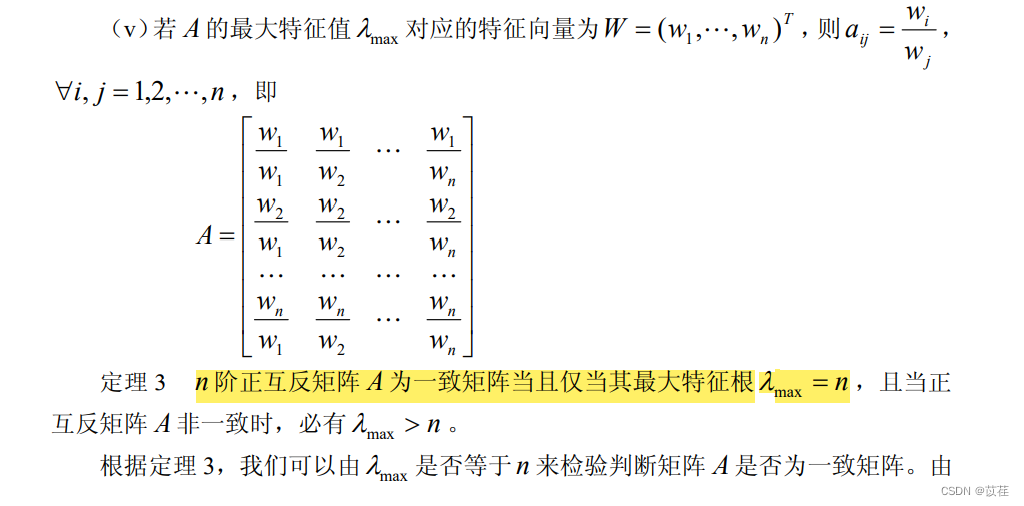





举例
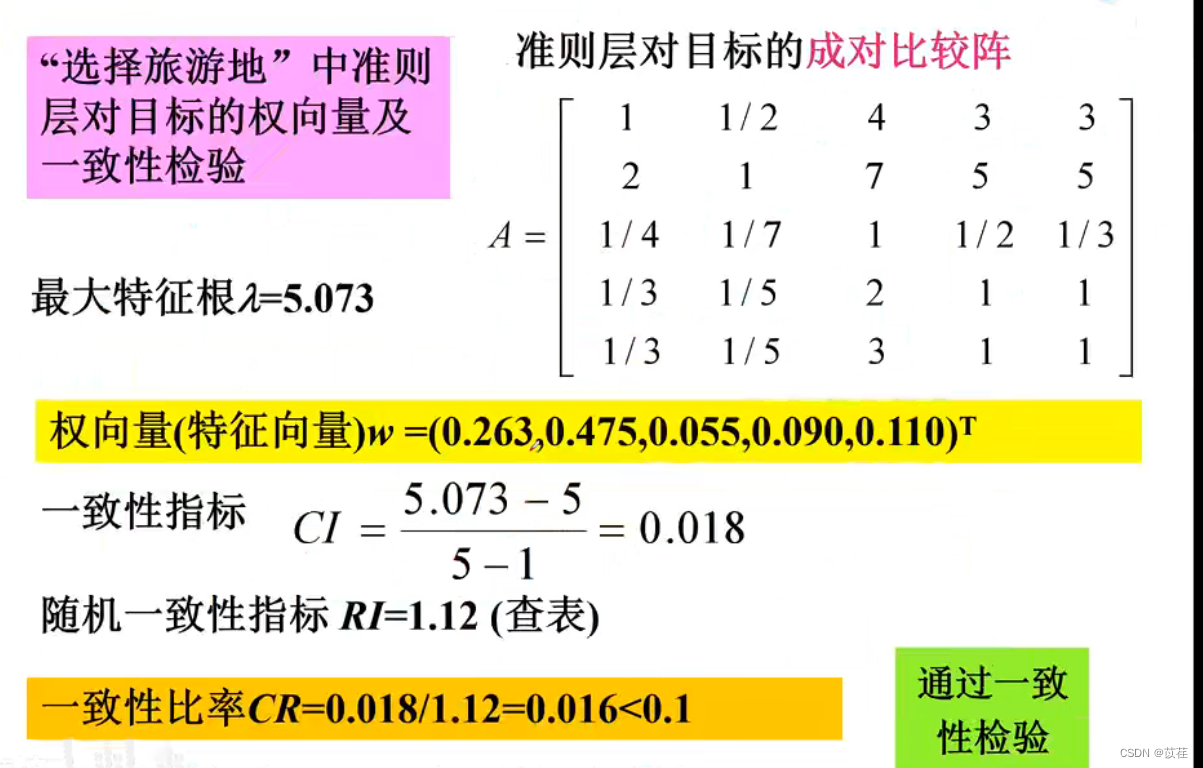
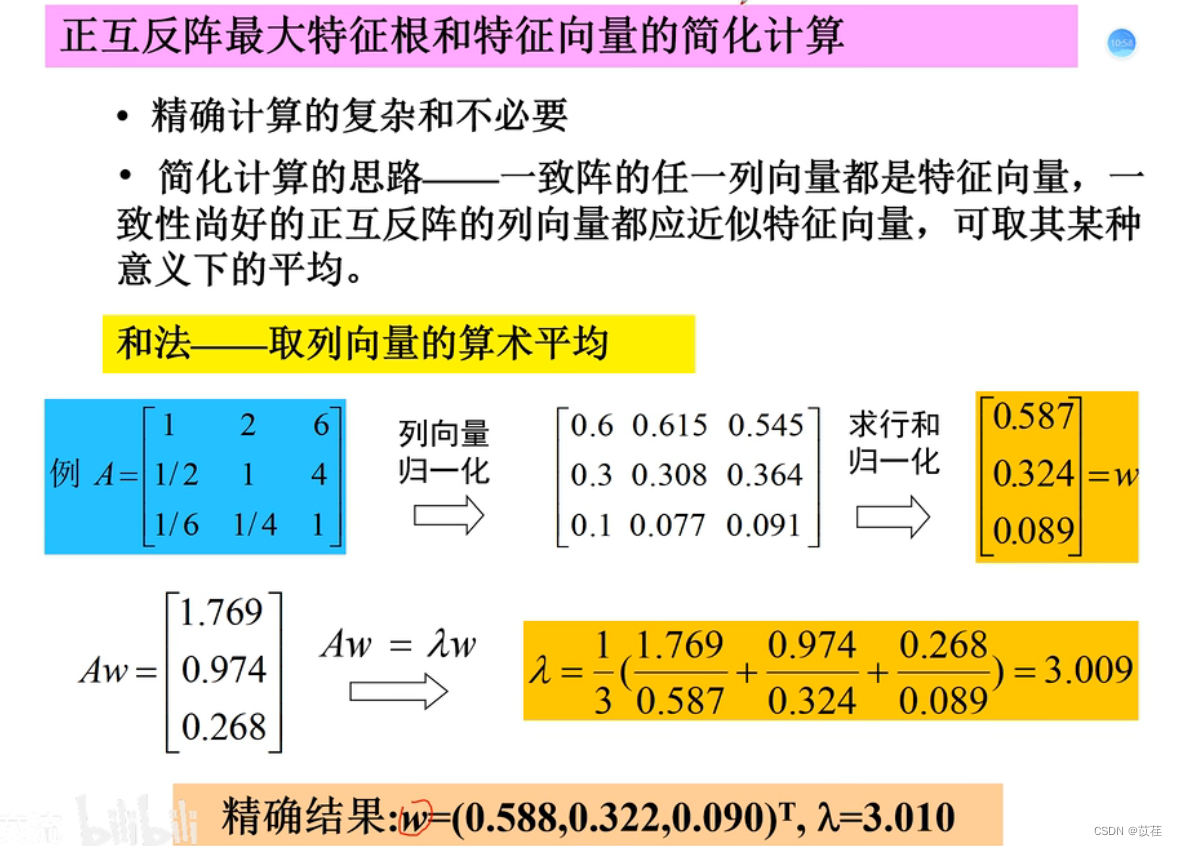
1.2 层次总排序及一致性检验
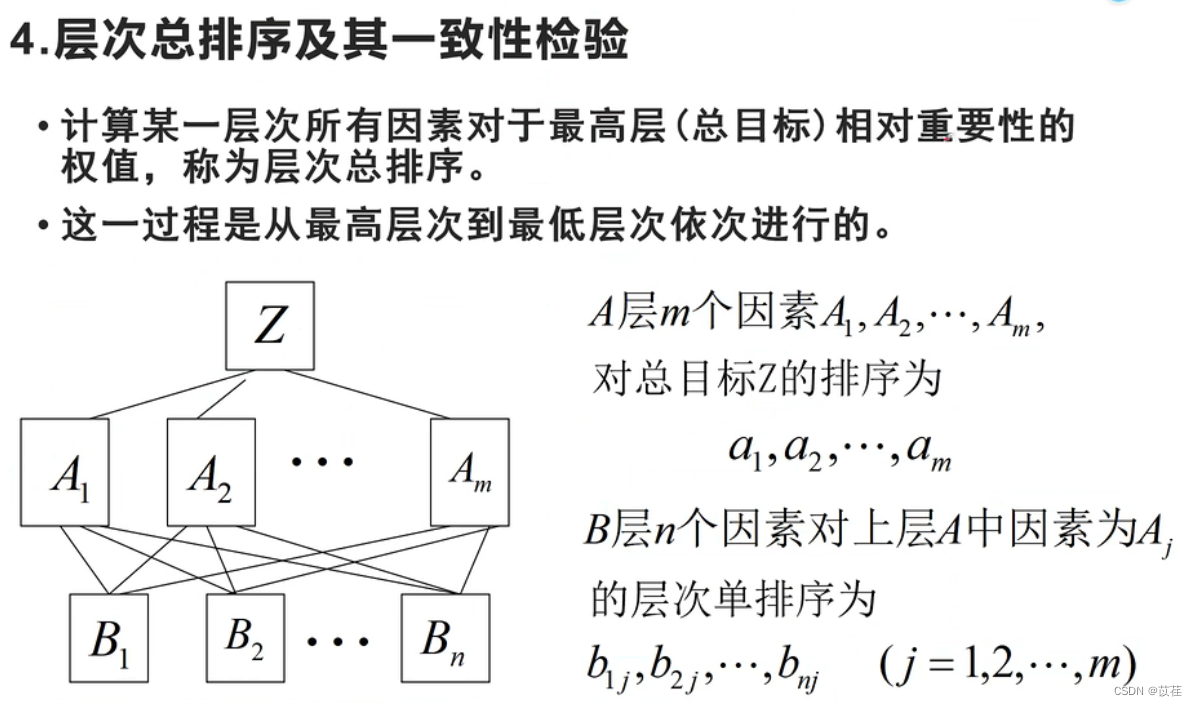
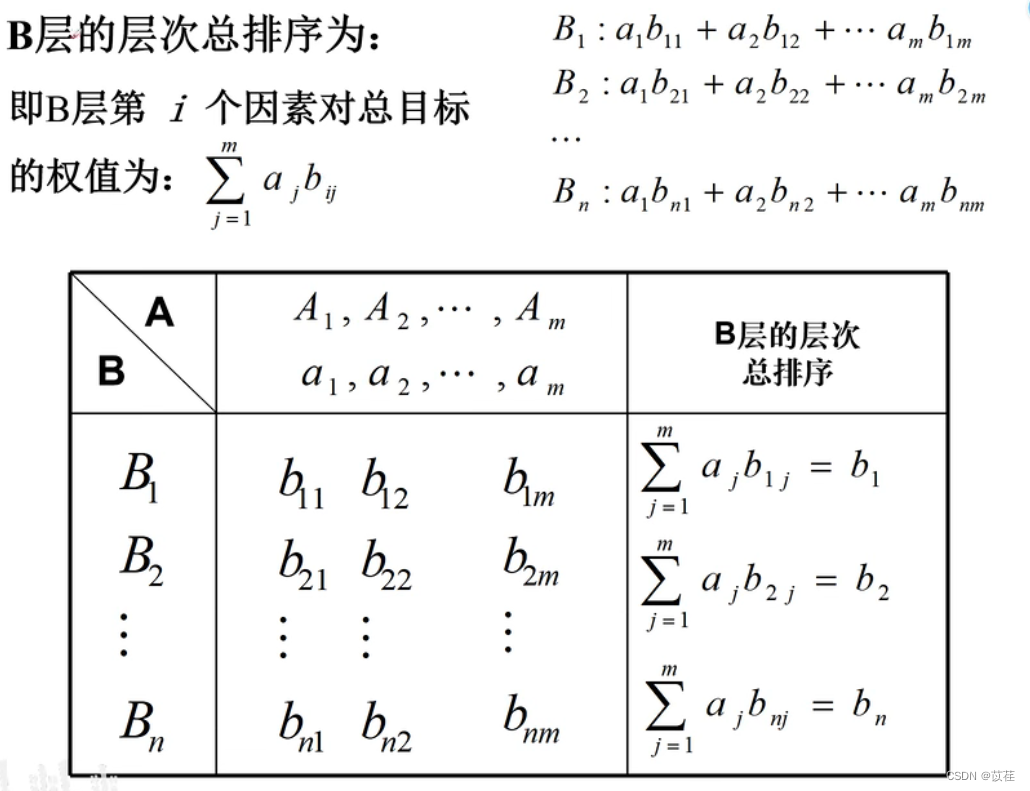

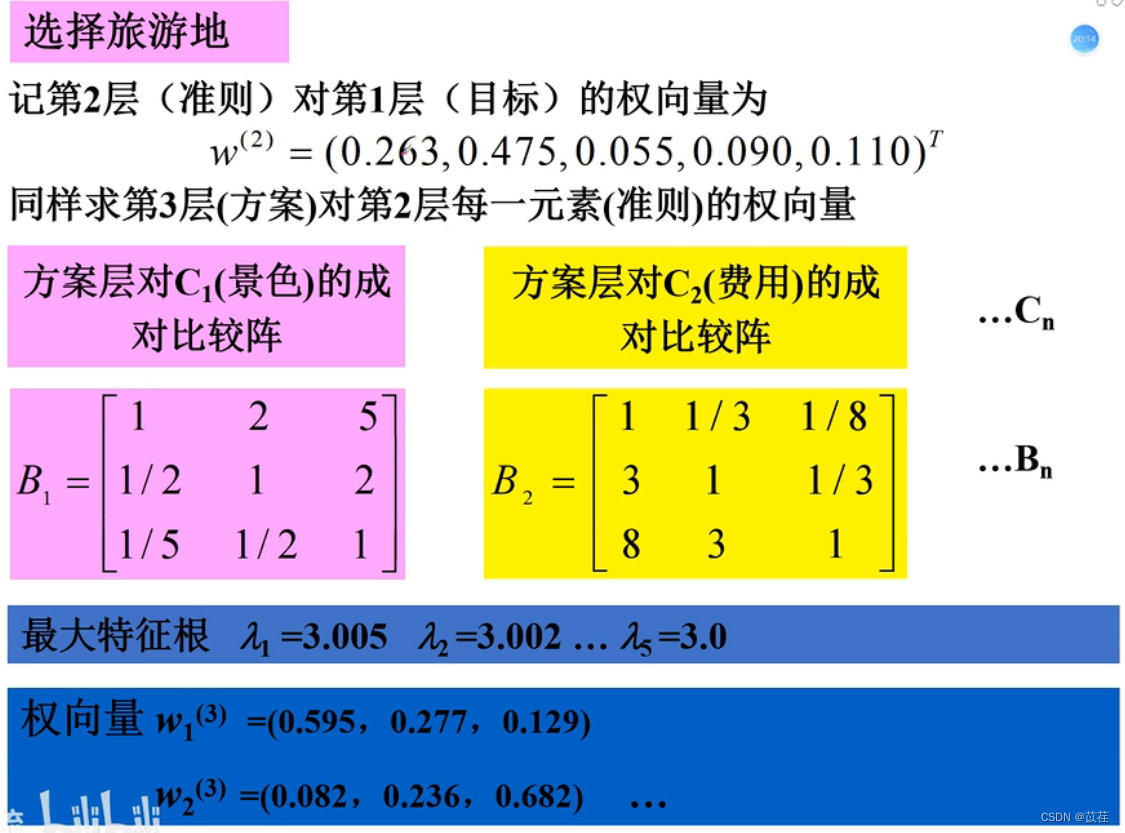
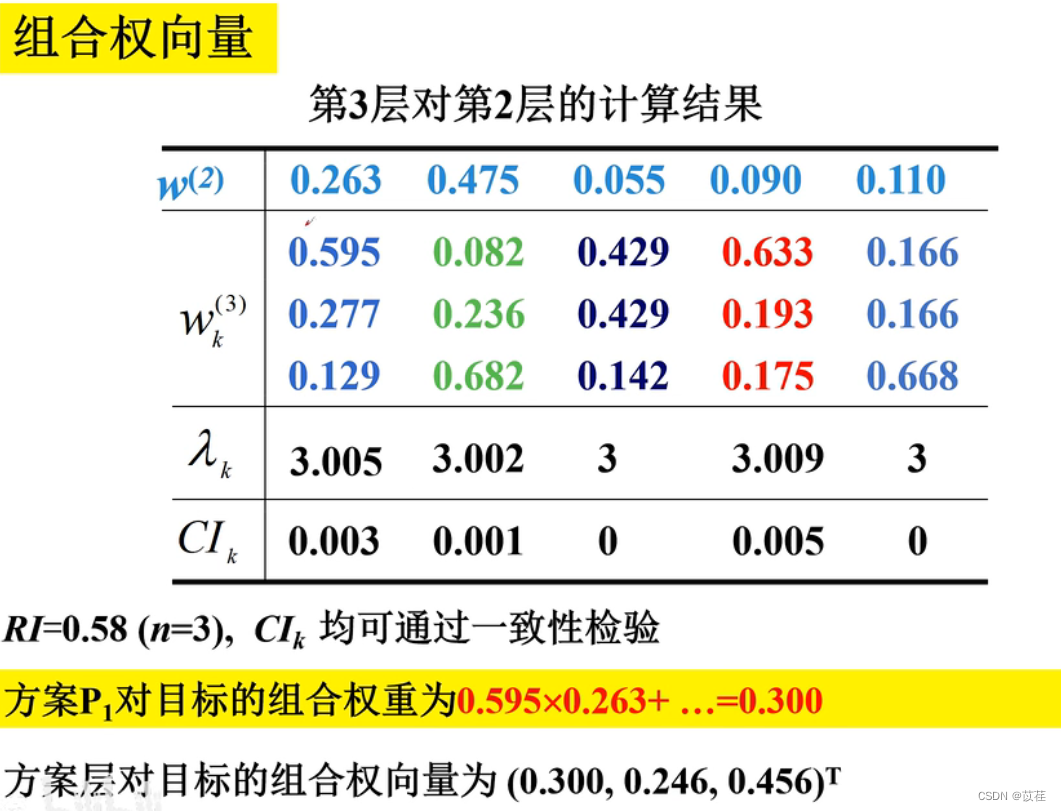
举例
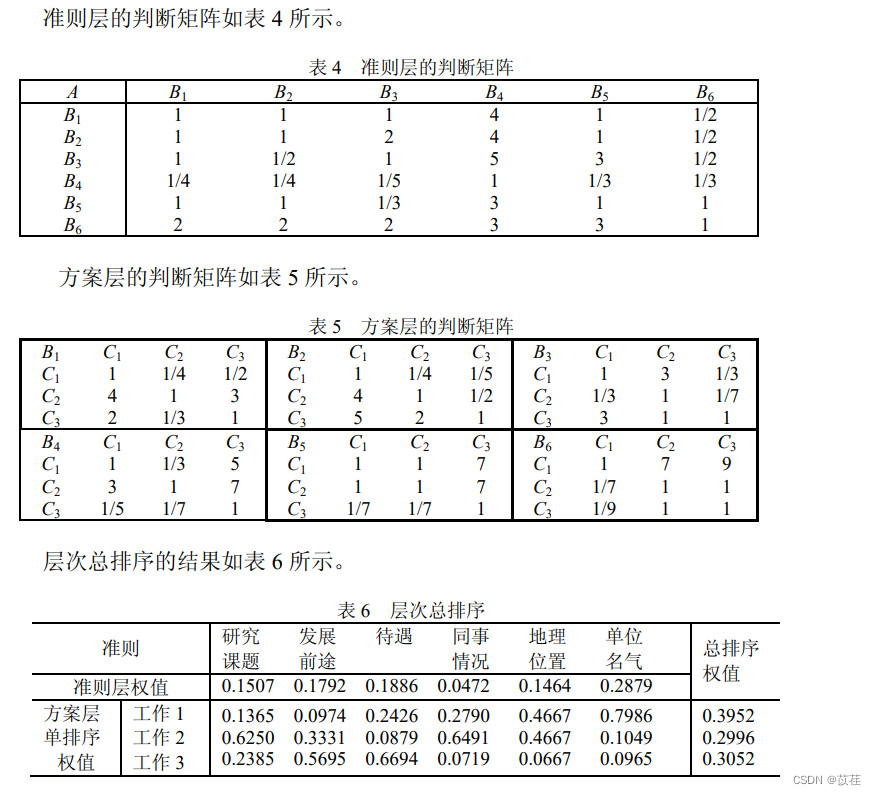
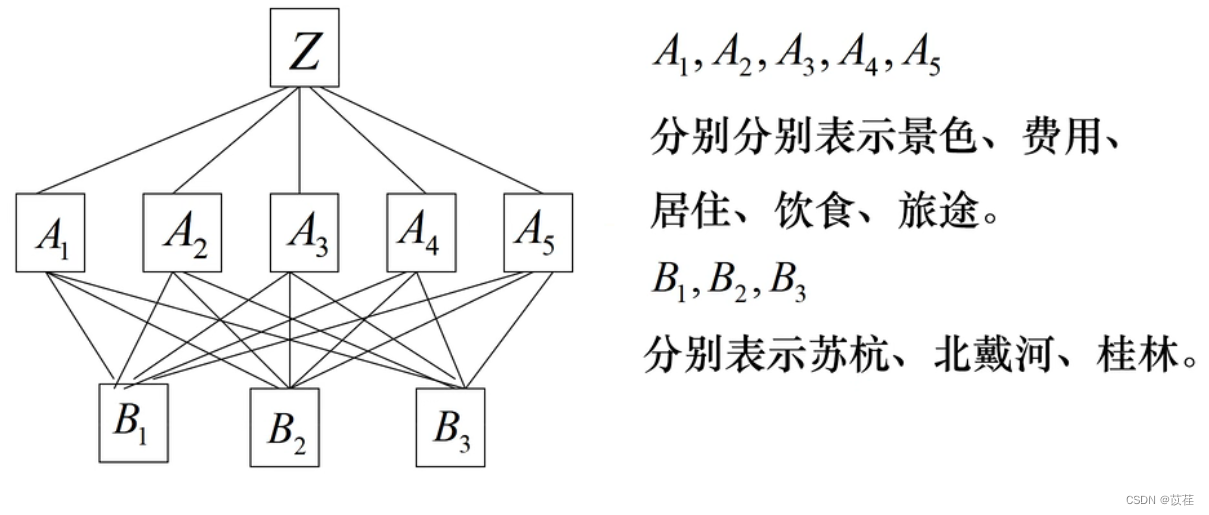
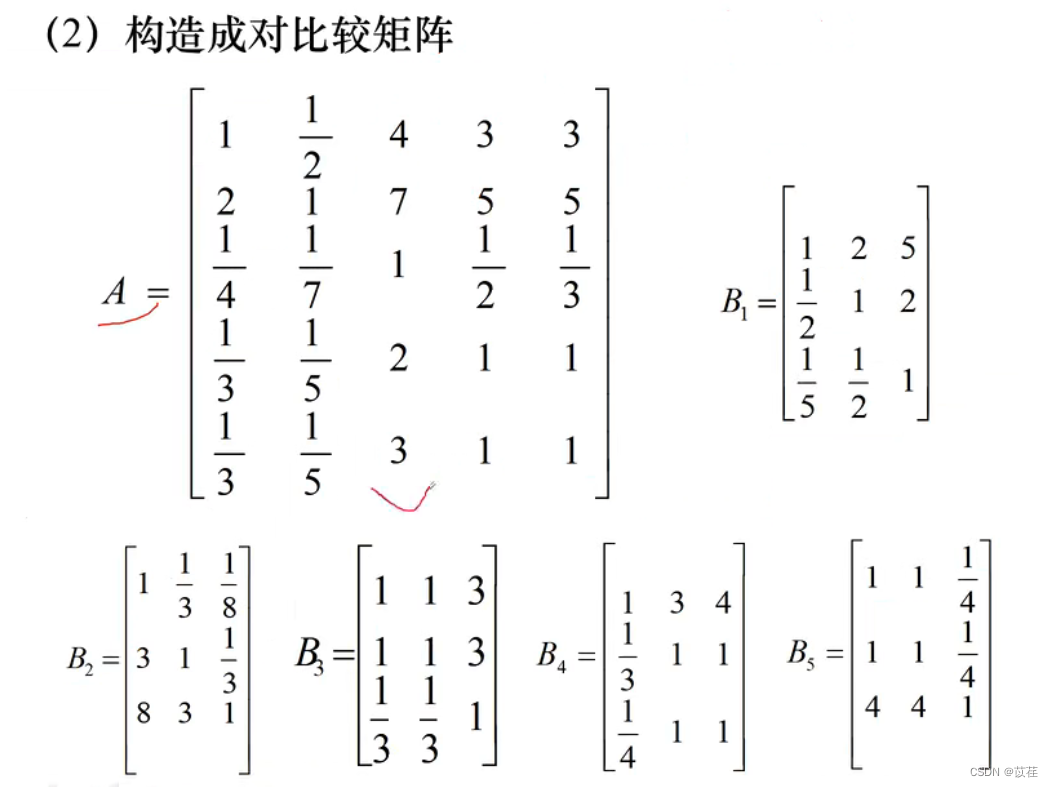
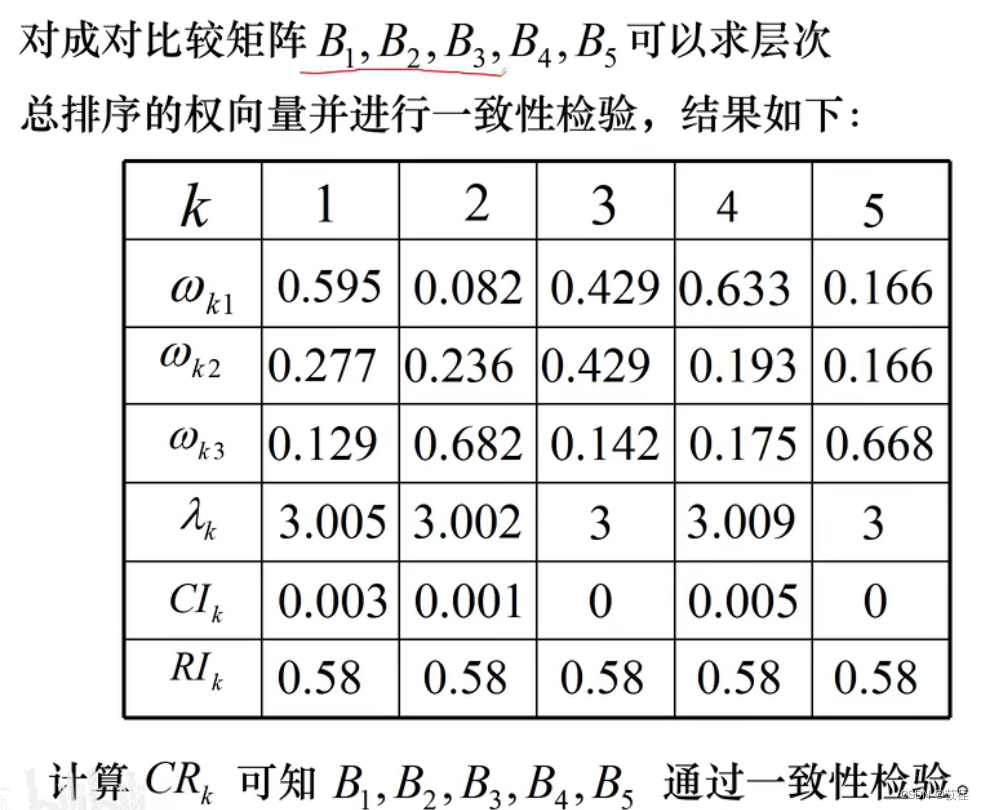
例 2 挑选合适的工作。经双方恳谈,已有三个单位表示愿意录用某毕业生。该
生根据已有信息建立了一个层次结构模型,如图 2 所示。
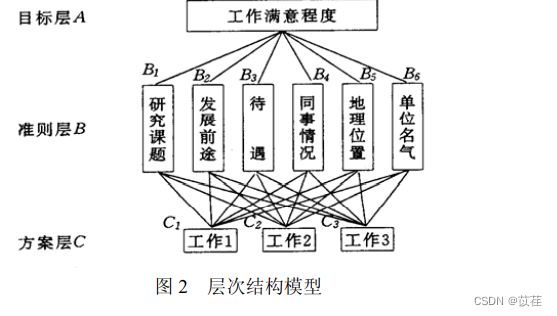
2. matlab代码
% 层次分析及一致性检验代码使用:%(1)构造判断矩阵A%(2)将下文代码复制粘贴到Matlab中即可% 例如:A=[1 3 5;0.33 1 3;0.2 0.33,1]disp('请输入准则层判断矩阵A(n阶)');A=input('A=');[n,n]=size(A); % 得到矩阵的阶数[V,D]=eig(A); % 求得特征向量和特征值% 求出最大特征值和它所对应的特征向量tempNum=D(1,1); % 特征值的初值pos=1; % 标记的第一个数for h=1:n if D(h,h)>tempNum tempNum=D(h,h); pos=h; % 最大特征值的位置 endendw=abs(V(:,pos)); % 找最大特征值对应的特征向量w=w/sum(w); % 归一化处理t=D(pos,pos); % t指的是最大的特征值disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);% 一致性检验CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];CR=CI/RI(n);if CR<0.10 disp('此矩阵的一致性可以接受!'); disp('CI=');disp(CI); disp('CR=');disp(CR);else disp('此矩阵的一致性验证失败,请重新进行评分!');end3. 应用过程举例



4. 参考资料
《数学建模算法与应用》(司守奎)《数学建模算法与应用习题解答》(司守奎)>> bilibili数学建模学习教程