1、求最大公约数和最小公倍数
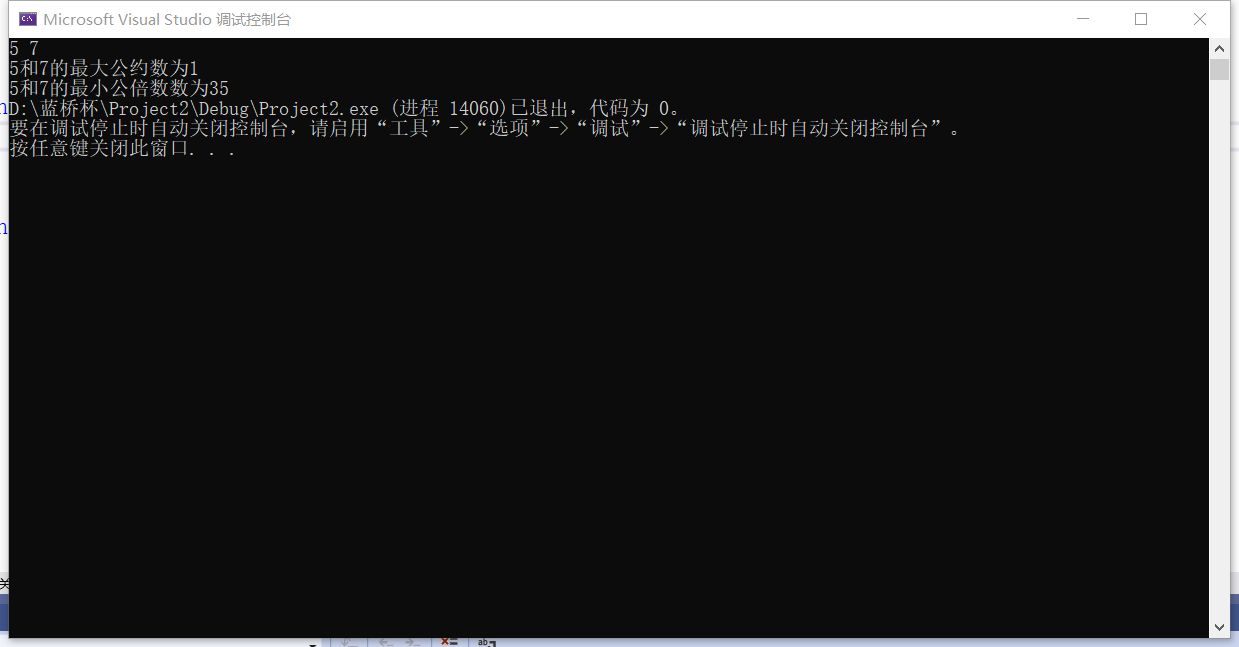
#include<iostream>using namespace std;int gcd(int a, int b)//最大公约数{ return b == 0 ? a : gcd(b, a % b);}int lcm(int a, int b)//最小公倍数{ return a * b / gcd(a, b);//a和b的乘积除与a和b的最大公约数}int main(){ int a, b; cin >> a >> b; cout <<a<<"和"<<b<<"的最大公约数为"<< gcd(a, b)<<endl; cout << a << "和" << b << "的最小公倍数数为" << lcm(a, b); return 0;}运行结果:
2、求素数(质数)
质数(prime number)又称素数,有无限个。一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,换句话说就是该数除了1和它本身以外不再有其他的因数;否则称为合数。
根据算术基本定理,每一个比1大的整数,要么本身是一个质数,要么可以写成一系列质数的乘积;而且如果不考虑这些质数在乘积中的顺序,那么写出来的形式是唯一的。最小的质数是2。
#include<iostream>using namespace std;bool isPrime(int n)//判断n是否为素数{ for (int i = 2; i*i <= n; i++) { if (n % i == 0) return false; } return true;}int main(){ int n; cin >> n; cout << "2---"<<n<<"之间的素数为:"; for (int i = 2; i <= n; i++) { if (isPrime(i)) cout << i << " "; } return 0;} 运行结果: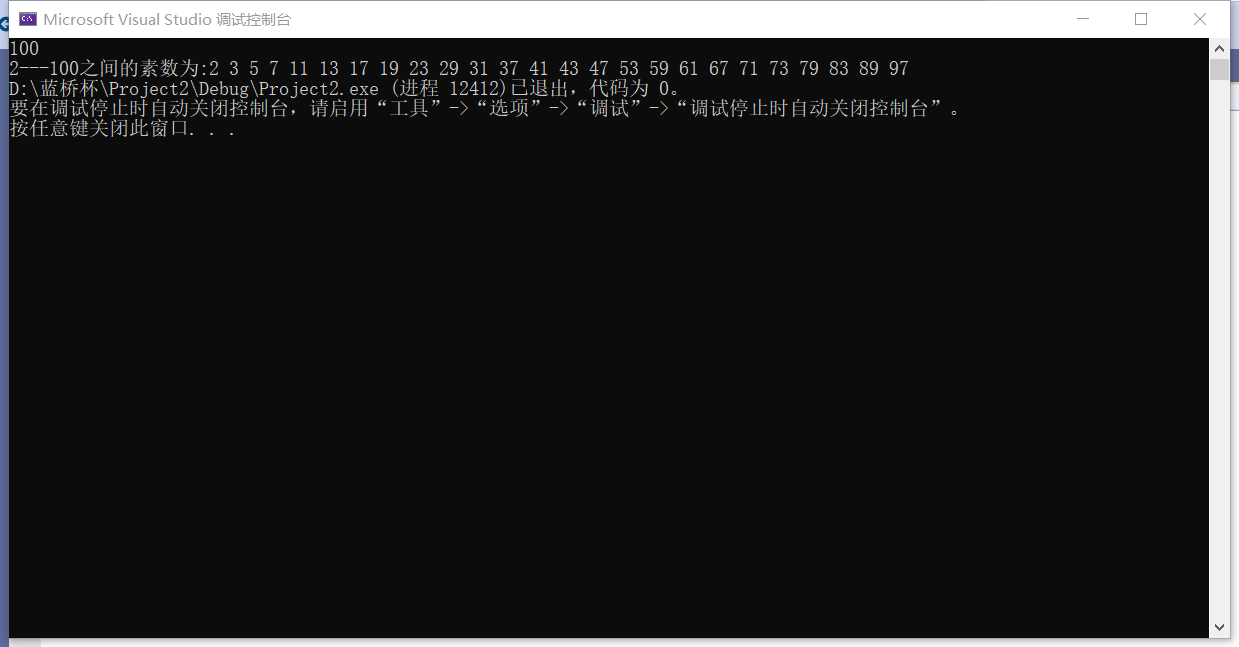
3、闰年
公历闰年判定遵循的规律为:四年一闰,百年不闰,四百年再闰。
既
bool Leaf(int x){return (x%400==0||(x%4==0&&x%100!=0));}
4、并查集
并查集在蓝桥杯用的还是比较多的。
常用的三个函数:
void init(int n){ for (int i = 1; i <= n; i++) { pre[i] = i;//初始化 }}int find(int x)//寻找根结点{ if (pre[x] == x) return x; return pre[x] = find(pre[x]);}void unit(int x, int y)//联合x,y{ int rx = find(x); int ry = find(y); if (rx != ry) pre[rx] = ry;}
例题(合根植物)及解析:
http://t.csdn.cn/sdZKv
5、差分法求解区间问题。
例题以及解析:
http://t.csdn.cn/uZBzC
6、前缀和求解区间问题。
例题以及解析:
http://t.csdn.cn/pkSl5
7、组合型枚举C(m,n)
代码:
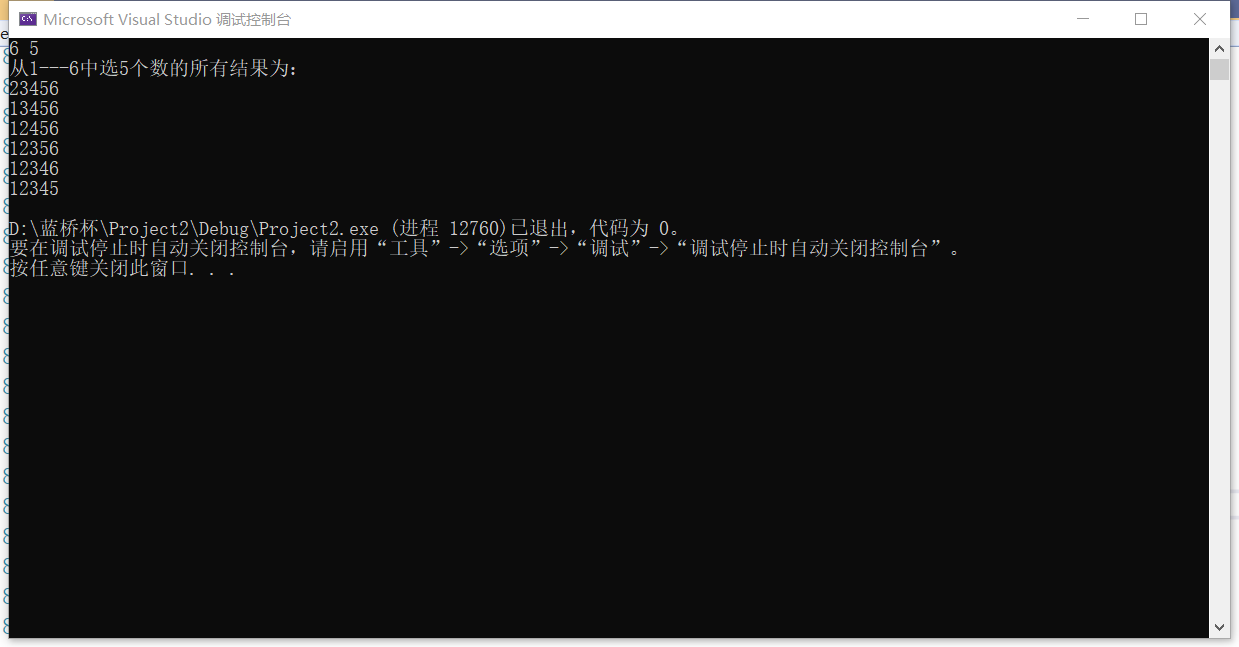
#include<iostream>#include<vector>using namespace std;int n;//共计N个数int m;//选m个数vector<int> ch;void Solve(int x) { if (ch.size() > m || ch.size() + (n - x + 1) < m) return; if (x == n + 1) { //选够了m个数输出 for (int i = 0; i < ch.size(); i++) cout << ch[i]; //也可以不输出,存放起来也是可以的,主要是看题目。 cout << endl; return; } Solve(x + 1); ch.push_back(x); Solve(x + 1); ch.pop_back();//消除痕迹}int main(){ cin >> n >> m; cout << "从1---" << n << "中选" << m << "个数的所有结果为:" << endl; Solve(1);}运行结果:
8、全排列问题
全排列问题解法有比较固定的模板,下面是链接(含题目和解析)
http://t.csdn.cn/EjnUy