基础知识
FFT即快速傅里叶变换,利用周期性和可约性,减少了DFT的运算量。常见的有按时间抽取的基2算法(DIT-FFT)按频率抽取的基2算法(DIF-FFT)。
1.利用自带函数fft进行快速傅里叶变换
若已知序列 x = [ 4 , 3 , 2 , 6 , 7 , 8 , 9 , 0 ] x=[4,3,2,6,7,8,9,0] x=[4,3,2,6,7,8,9,0],求 X ( k ) = D F T [ x ( n ) ] X(k)=DFT[x(n)] X(k)=DFT[x(n)]
代码非常简单,只有两行
x=[4,3,2,6,7,8,9,0];xk=fft(x)
一般,对MATLAB而言,要想让它显示出结果,计算的部分不要加分号。
2.绘制128点DFT的幅频图
已知信号由15Hz幅值0.5的正弦信号和40Hz幅值2的正弦信号组成,数据采样频率为100Hz,试绘制N=128点DFT的幅频图。
关于下列代码的解释
f=(0:N-1)'*fs/N;其中(0:N-1)'是生成了一个长度为N,间隔为1的列向量转置所得到的行向量。fs/N是指频域上的频率间隔。
若N点序列x(n)(n=0,1,…,N-1)是在采样频率fs(Hz)下获得的。它的FFT也是N点序列,即X(k)(k=0,1,…,N-1),则第K点对应实际频率值为:
f=k*fs/N
clc;fs=100;Ts=1/fs;%采样时间间隔N=128;n=0:N-1;t=n*Ts; %x不是直接关于n的函数,因为是固定的采样时间点x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);y=fft(x,N);f=(0:N-1)'*fs/N;stem(f,abs(y));运行结果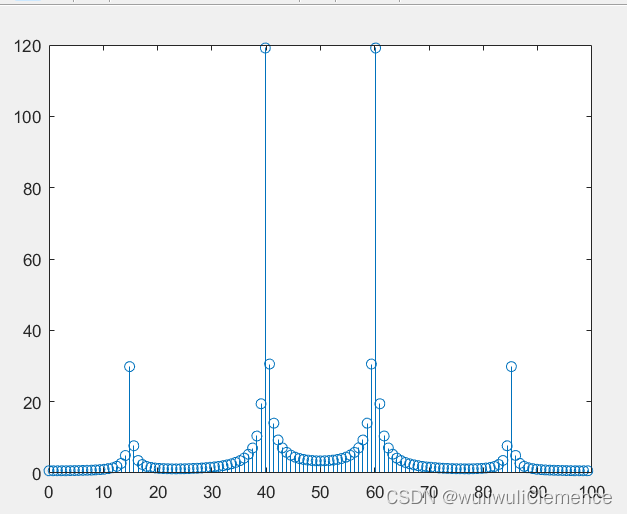
同时也可以可看到这个幅度谱是关于fN对称的。
3.利用FFT进行功率谱的噪声分析
已知带有测量噪声信号 x ( t ) = s i n ( 2 π f 1 t ) + s i n ( 2 π f 2 t ) + 2 w ( t ) x(t)=sin(2πf1t)+sin(2πf2t)+2w(t) x(t)=sin(2πf1t)+sin(2πf2t)+2w(t) 其中f1=50Hz,f2=120Hz, w(t)为均值为零、方差为1的随机信号,采样频率为1000Hz,数据点数N=512。试绘制信号的功率谱图。
下面先介绍几个基本的函数和知识:
conj(Y)
conj(Y) 是 MATLAB 中的一个函数,表示对 Y 中的每个元素取其共轭复数。如果 Y 是一个实数数组,则返回其本身。在信号处理中,常常使用共轭复数进行频域变换的处理。
求功率
P=Y.*conj(Y)/512;
注意这里是点乘啊。
在信号处理中,功率可以表示为信号的平均能量。对于一个离散时间信号,其能量可以表示为其幅度平方的总和,即:
E = ∑ n = 0 N − 1 ∣ x [ n ] ∣ 2 E = \sum_{n=0}^{N-1} |x[n]|^2 E=n=0∑N−1∣x[n]∣2
其中, N N N 是信号的抽样点数, x [ n ] x[n] x[n] 是信号在时刻 n n n 的采样值。这里的 ∣ x [ n ] ∣ 2 |x[n]|^2 ∣x[n]∣2 表示对 x [ n ] x[n] x[n] 取模长平方。
如果要计算信号的平均功率,可以将其总能量除以抽样点数,即:
P = E N = 1 N ∑ n = 0 N − 1 ∣ x [ n ] ∣ 2 P = \frac{E}{N} = \frac{1}{N} \sum_{n=0}^{N-1} |x[n]|^2 P=NE=N1n=0∑N−1∣x[n]∣2
这里的 P P P 表示信号的功率。
在代码中, Y Y Y 表示信号的离散傅里叶变换,即频域表示,其幅度 ∣ Y ∣ |Y| ∣Y∣ 表示信号在每个频率分量上的贡献。为了计算信号的功率谱,需要将 Y Y Y 变换为其幅度平方,即 ∣ Y ∣ 2 |Y|^2 ∣Y∣2。由于 Y Y Y 中包含了正频率和负频率的信息,因此需要对其进行共轭操作,即将负频率部分取共轭复数,然后再与正频率部分相乘,即 Y ⋅ conj ( Y ) Y \cdot \operatorname{conj}(Y) Y⋅conj(Y)。最后将结果除以抽样点数 N N N,即可得到功率谱 P P P:
P = Y ⋅ conj ( Y ) N P = \frac{Y \cdot \operatorname{conj}(Y)}{N} P=NY⋅conj(Y)
这里的 P P P 是一个长度为 N N N 的向量,表示信号在每个频率分量上的功率。
randn
andn是MATLAB中的一个函数,用于生成一个均值为0,方差为1的标准正态分布随机数。例如,可以使用以下代码生成一个大小为3x3的标准正态分布随机矩阵:
A = randn(3,3);
完整代码
clc;t=0:0.001:0.6;%设置步进与时间区间x=sin(2*pi*50*t)+sin(2*pi*120*t);%根据已知写出信号的表达式noise=randn(1,length(t));%生成均值为零、方差为1的随机信号,也就是噪声y=x+noise;%带有噪声的信号subplot(121);plot(t,y);fs=1000;Y=fft(y,512);%512点的FFTP=Y.*conj(Y)/512;%求功率f=(0:255)*fs/256%由上面的分析可知,频谱关于奈奎斯特频率对称,所以取其中一半subplot(122);plot(f,P(1:256))%功率随频率的变化,即功率谱图,绘制出一半运行结果: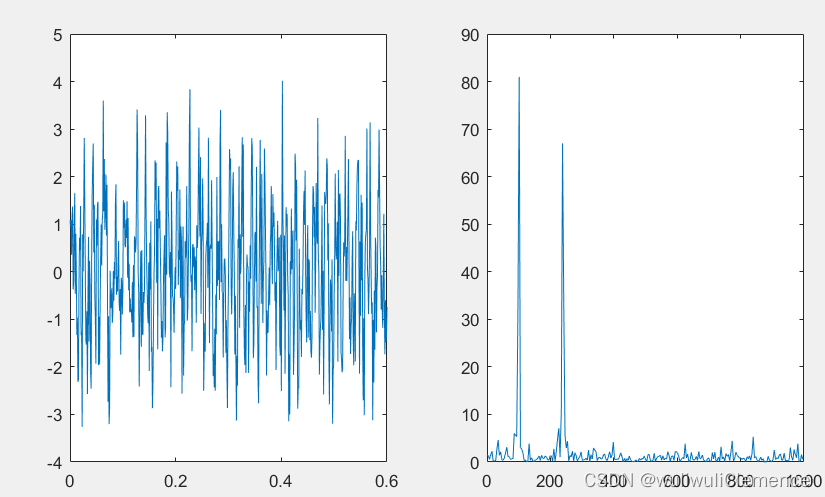
4.序列长度和FFT的长度对信号频谱的影响
已知信号 x ( t ) = 0.5 s i n ( 2 π f 1 t ) + 2 s i n ( 2 π f 2 t ) x(t)=0.5sin(2πf1t)+2sin(2πf2t) x(t)=0.5sin(2πf1t)+2sin(2πf2t)
其中f1=15Hz,f2=40Hz,采样频率为100Hz.
在下列情况下绘制其幅频谱。
有了前面的基础,这里就比较简单了
代码
nlength=32;nfft1=32;nfft2=128;fs=100;Ts=1/fs;n=0:nlength-1;t=n*Ts;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);y1=fft(x,nfft1);f1=(0:31)*fs/32;subplot(211);Y1=abs(y1);plot(f1(1:16),Y1(1:16));y2=fft(x,nfft2);f2=(0:127)*fs/128;subplot(212);Y2=abs(y2);plot(f2(1:64),Y2(1:64));运行结果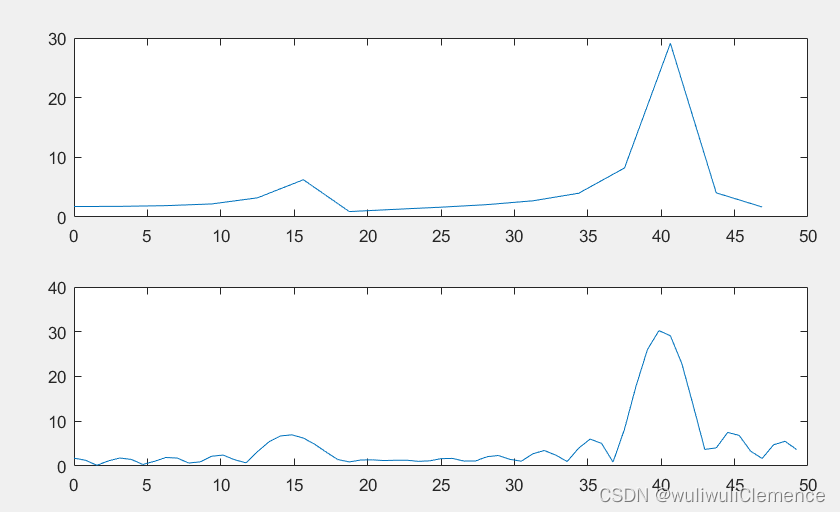
结果分析
采样点数越多,其频谱越光滑。
注意
绘制图形的时候,一定要分析清楚是频谱图,还是某一个变换,其目的在于分清谁是因变量,谁是自变量。