题目链接
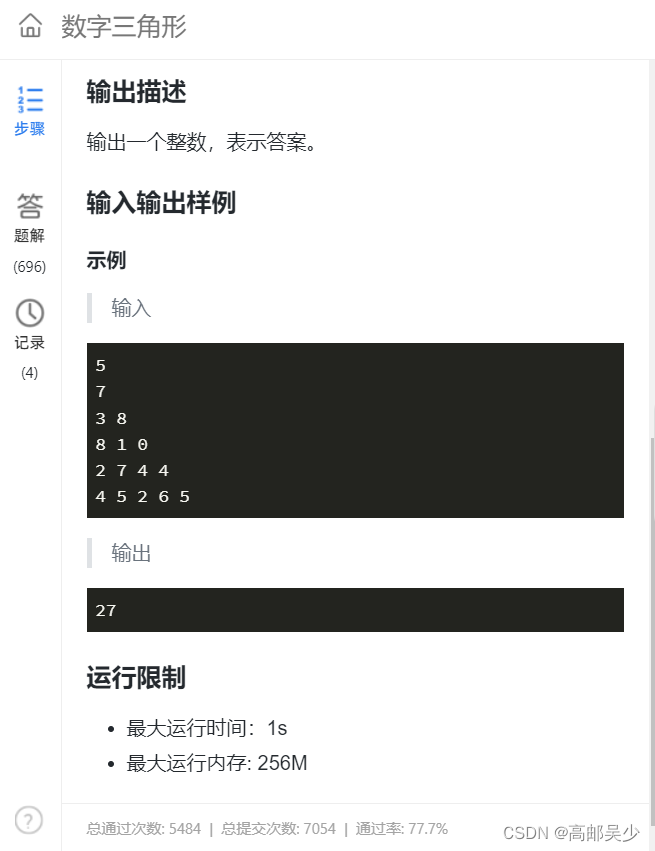
解题思路: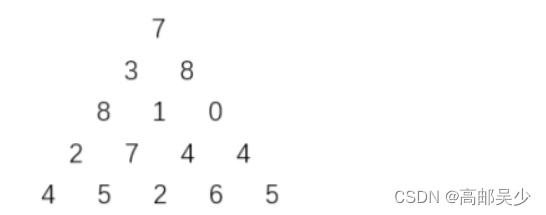
该题是一道经典的动态规划,对于这样的数字三角形,
我们用一个数组arr存储各个位置的数字,再用另一个数组brr来记录到该位置的最大路径
对于图中的7,我们用数组保存就是arr[0][0]
对于图中的8,也就是arr[1][1]
情况1:走到最左边一列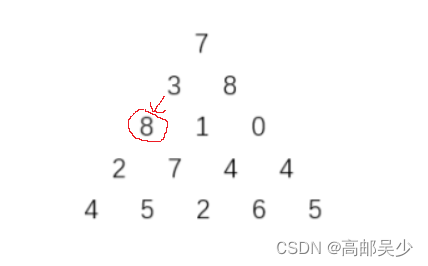
这种情况只可能是上一行最左边一列走过来的,如图
以上图为例:
我们brr现在开始从起点7出发,因为起点只有一个,也就是把arr的值7赋给brr[0][0]
然后假设我们从7往左走到3,也就是arr[0][0]走向arr[1][0],我们可以记录brr[1][0]=brr[0][0]+arr[1][0]
对于其他的路径走到最左边一列,那都是brr[i][0] = brr[i - 1][0]+ arr[i][0],
brr[i - 1][0]是之前走过的最大长度,arr[i][0]是当前节点的长度
情况2:走到中间列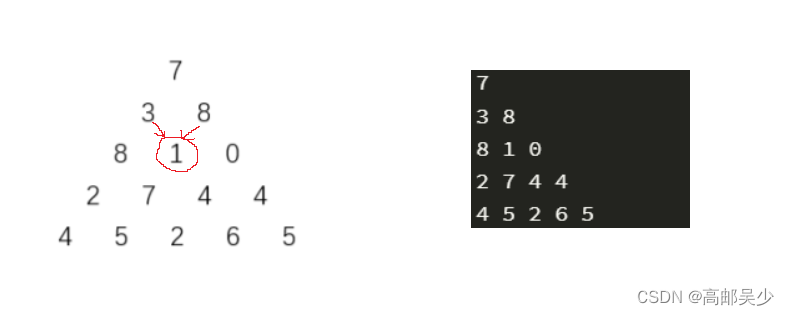
假设现在走到了1,1是有两条路可以走过来的,一个是3过来的,一个是8过来的。
我们brr是要到这1这个节点的最大值啊,所以需要对3过来的路和8过来的路大小进行比较
对应到arr数组中就是brr[2][1]=max(brr[1][0],brr[1][1])+arr[2][1]
推广开来就是 brr[i][j] = max(brr[i - 1][j - 1], brr[i - 1][j]) + arr[i][j]
情况3:走到最右边一列
这种和情况1类似,只能有上一行最右边走过来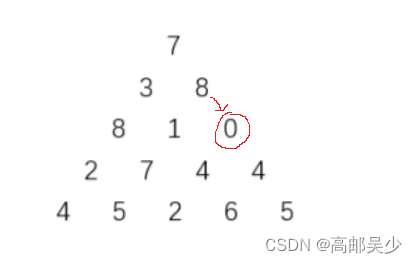
推广公式为brr[i][j] = brr[i - 1][j - 1] + arr[i][j]
代码如下:
```c#include <stdio.h>#include <stdlib.h>int max(int x,int y){ return x>y?x:y;}int main(int argc, char *argv[]){// 请在此输入您的代码int arr[100][100];int brr[100][100];int n = 0;int i = 0;int j = 0;scanf("%d", &n);for (i = 0;i < n;i++){for (j = 0;j <= i;j++){scanf("%d", &arr[i][j]);}}brr[0][0] = arr[0][0];for (i = 1;i < n;i++){for (j = 0;j <= i;j++){if (j == 0)//第一列的情况{brr[i][j] = brr[i - 1][j]+ arr[i][j];}else if (j != 0 && j != i)//中间列的情况{brr[i][j] = max(brr[i - 1][j - 1], brr[i - 1][j]) + arr[i][j];}else//最后一列的情况{brr[i][j] = brr[i - 1][j - 1] + arr[i][j];}}}if (n % 2 != 0) //如果行数是奇数,最后会走到最后一行中间的数{printf("%d", brr[n - 1][(n - 1) / 2]);}else {//如果行数是偶数,最后取中间两个较大值即可printf("%d", max(brr[n - 1][(n - 1) / 2], brr[n - 1][n / 2]));}return 0;}