本文章内容只作为个人学习总结使用。

目录

说明：

基本的FFT使用方法：

        1、简单的FFT功能介绍：

        2、恢复幅度轴，创建频率轴：

说明：

        本文章主要进行MATLAB中fft函数基本使用方法的讨论，关于fft的概念以及为什么要进行fft等信号处理方面的内容不做叙述。

基本的FFT使用方法：

        1、简单的FFT功能介绍：

        在这一步我们首先需要构建一个正弦函数f=sin（2*pi*f*t）不难看出本例中的正弦函数的频率为1，其中fs是我们的采样频率，当采样频率为100的时候 我们的采样周期1/fs 为0.01s 也就是每隔0.01s取一个点。

clear;fs=100;%采样频率t=0:1/fs:10-1/fs %采样周期%%原始信号的创建f=sin(2*pi*1*t);subplot(311)plot(t,f)%%fft部分(1) 此时我们其实可以发现他的幅度不对横轴也不对。f_fft=fft(f);f_amp=abs(f_fft);subplot(312);plot(f_amp);

运行结果：

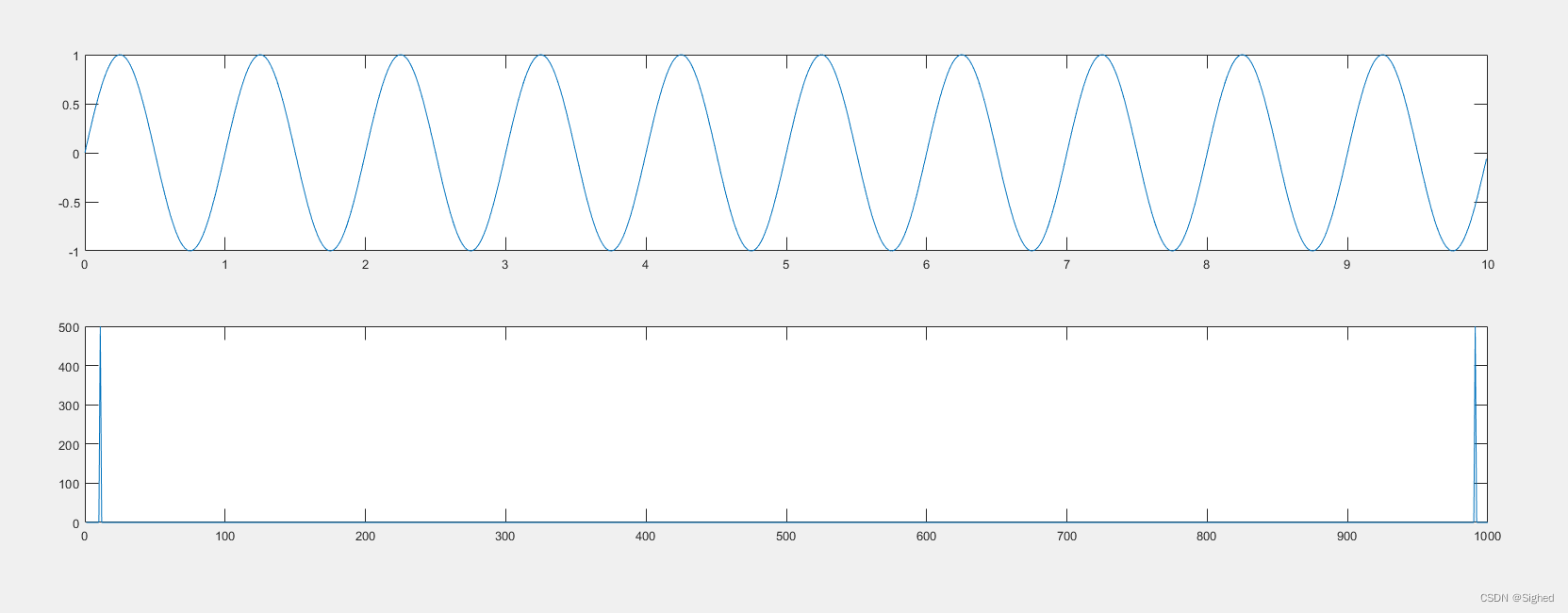
可以看到，在信号创建的部分我们创建了一个1hz的正弦波，关于MATLAB中fft的函数使用非常简单，只需要fft（f）就可以将信号进行fft变换，在变量去也可以看到计算结果是1000个复数，其中有几个点我们可以重点关注一下：他的第一个点和第501个点（因为在本例中我们取了1000，如果取其他偶数点的情况此例就变成其他长度的中点 例如10000点就是5001点）这两个点都是实数，同时可以发现除了第一个点其余的点关于501点共轭对称关于这两个点在后面会用到。

上述代码貌似很轻松的实现了fft的功能但是只要稍微的观察就可以发现他的幅度和频率是不对的（如上图），双边谱来说幅度应该是0.5每边而且他的横轴是数据点数而不是频率，这是我们首先要处理的一个问题：幅度量纲归为，频率轴设定。

        2、恢复幅度轴，创建频率轴：

        在这一部分，我将主要介绍如何恢复单边谱的频率轴和幅度，关于单边谱和双边谱是什么，有需要的可以自行参阅任何一本信号与系统教材，这里只讲MATLAB中的处理。

        首先第一个问题，为什么他的幅度是不对的呢？根据我查到的资料其中有提到的是在dft的公式中，其实已经蕴含了1/N项，但是MATLAB中fft算法并没有，所以其计算出来的幅值是大了N倍，我们将其除以N就可以了。

        第二个如何恢复频率轴，直接绘图，MATLAB会默认将我们的点数N作为横轴，这其实是不对的，我们的横轴应该是频率f，那么f怎么创建呢，我们不妨这样理解，我们以采样频率Fs=100Hz采样了N=1000个点 那每个点代表的频率就是df=Fs/N以单边谱为例，那我们所需的f轴就只需要我们用df*我们创建的点数（包括正负）就可以了，上个部分中我们说过，我们的fft的结果是关于N/2+1共轭对称的，所以我们只只取其对称的一部分就可以了。

clear;fs=100;%采样频率t=0:1/fs:10-1/fs%采样周期%%原始信号的创建f=sin(2*pi*10*t);subplot(311)plot(t,f)%%fftf_fft=fft(f);N=length(f_fft);%这里取出f_fft也就是信号做完fft之后的序列长度Y=f_fft(1:N/2+1);Y(2:end-1)=2*Y(2:end-1);Y_amp=abs(Y)/N;df=fs/N;f=(0:1:N/2)*df;subplot(312);plot(f,Y_amp)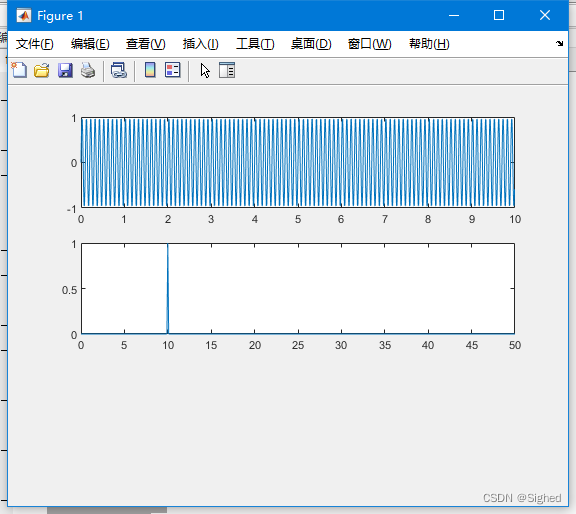

至此我们就绘制出了频率幅度都正确的单边谱。