目录
试题A:裁纸刀试题B:灭鼠先锋试题C:求和试题 D: 选数异或试题 E: 爬树的甲壳虫试题 F: 青蛙过河试题 G: 最长不下降子序列试题 H: 扫描游戏试题 I: 数的拆分试题 J: 推导部分和
试题A:裁纸刀
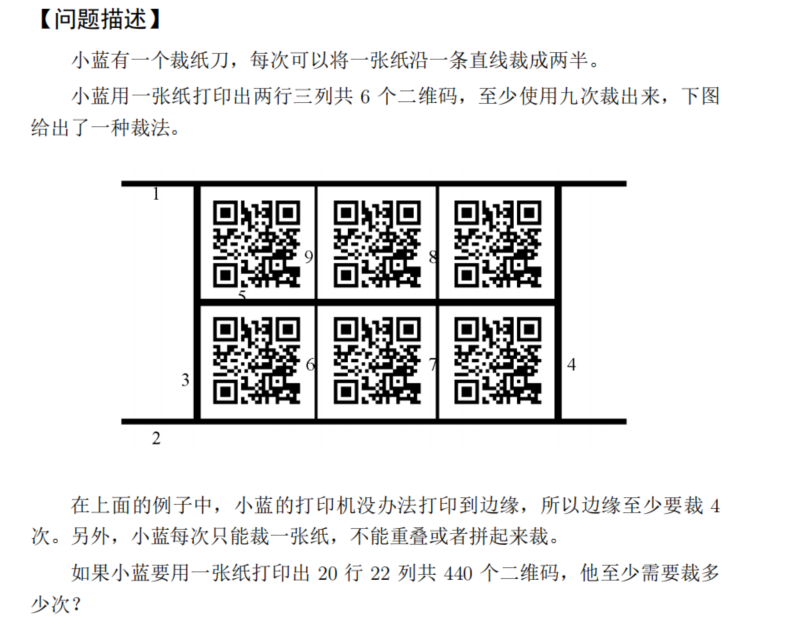
答案为 n ∗ m − 1 + 4 n*m-1+4 n∗m−1+4
443
试题B:灭鼠先锋

LLLV
试题C:求和

预计得分100%
思路:维护一个前缀 s u m sum sum即可。
总时间复杂度 O ( n ) O(n) O(n)
参考代码:
#include <bits/stdc++.h>using namespace std;const int N = 2e5 + 5;int a[N];void solve(){ int n; scanf("%d", &n); long long ans = 0, sum = 0; for (int i = 1; i <= n; i++) { scanf("%d", &a[i]); ans += sum * a[i]; sum += a[i]; } cout << ans << endl;}int main(){ solve(); return 0;}试题 D: 选数异或

预计得分100%
对于每个位置 i i i ,设 y = a [ i ] y = a[i] y=a[i] ^ x x x,找到最近的一个 y y y的下标 i d x idx idx,记作 b [ i ] b[i] b[i]。再用线段树维护 b b b数组的区间最大值 m a x x maxx maxx,如果 m a x x > = L maxx >= L maxx>=L,那么为 y e s yes yes。
总时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
参考代码:
#include <bits/stdc++.h>using namespace std;const int N = 3e5 + 5;int a[N], b[N];struct node{ int l, r, val, maxx;} tr[N * 4];void pushup(int k) { tr[k].maxx = max(tr[k * 2].maxx, tr[k * 2 + 1].maxx); }void build(int k, int l, int r){ tr[k].l = l; tr[k].r = r; if (tr[k].l == tr[k].r) { tr[k].val = tr[k].maxx = b[l]; return; } int mid = l + r >> 1; build(k * 2, l, mid); build(k * 2 + 1, mid + 1, r); pushup(k);}int query(int k, int l, int r){ if (tr[k].l == l && tr[k].r == r) return tr[k].maxx; int mid = tr[k].l + tr[k].r >> 1; if (r <= mid) return query(k * 2, l, r); else if (l > mid) return query(k * 2 + 1, l, r); else return max(query(k * 2, l, mid), query(k * 2 + 1, mid + 1, r));}void solve(){ int n, m, x; scanf("%d %d %d", &n, &m, &x); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); map<int, int> last; for (int i = 1; i <= n; i++) { int y = a[i] ^ x; if (!last.count(y)) b[i] = -1; else b[i] = last[y]; last[a[i]] = i; } build(1, 1, n); while (m--) { int l, r; scanf("%d %d", &l, &r); int maxx_pos = query(1, l, r); puts(maxx_pos >= l ? "yes" : "no"); }}int main(){ solve(); return 0;}试题 E: 爬树的甲壳虫

暂时不会。
试题 F: 青蛙过河

2022.4.25 UPDATE:少了一个语句,已修正
预计得分100%
二分经典题改编题,一眼二分,check有点难写。
check思路:
可以令 d p [ i ] dp[i] dp[i]表示跳到第 i i i个石头的最大次数。
把最后 m i d mid mid个石头的 d p [ i ] dp[i] dp[i]加起来, s u m > = 2 ∗ x sum>= 2*x sum>=2∗x即合法。
总时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
参考代码:
#include <bits/stdc++.h>using namespace std;const int N = 3e5 + 5;int a[N];long long dp[N];// dp[i]表示最多能跳到位置i dp[i]次int n, x;bool check(int mid){ long long sum = 0; for (int i = 1; i <= mid; i++) //前mid个都可以 dp[i] = a[i]; int l = 1; for (int i = mid + 1; i <= n; i++) { while (i - l > mid)//控制跳跃距离。 ++l; dp[i] = 0; while (dp[i] < a[i] && l < i) { if (dp[l] + dp[i] <= a[i]) { dp[i] += dp[l]; dp[l] = 0; ++l; } else { dp[l] -= a[i] - dp[i]; dp[i] = a[i]; } } } long long ans = 0; int L = n - mid + 1; for (int i = L; i <= n; i++) ans += dp[i]; return ans >= 2 * x;}void solve(){ scanf("%d %d", &n, &x); --n; for (int i = 1; i <= n; i++) scanf("%d", &a[i]); int l = 1, r = n, ans = n + 1; while (l <= r) { int mid = l + r >> 1; if (check(mid)) { ans = mid; r = mid - 1; } else l = mid + 1; } printf("%d\n", ans);}int main(){ solve(); return 0;}试题 G: 最长不下降子序列

预计得分10% ~ 30%
暴力思路:
枚举修改位置,二分法 O ( n l o g n ) O(nlogn) O(nlogn)求最长不下降子序列,(跳过中间那段长度为 k k k的数组)
总时间复杂度 O ( n 2 l o g n ) O(n^2logn) O(n2logn)
参考代码:
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 5;int a[N], dp[N];int n, k;int LIS(int L, int R) //二分求LIS{ int len = 0; dp[len] = -0x3f3f3f3f; for (int i = 1; i <= n; i++) { if (i == L) //跳过k个 { i = R; continue; } if (a[i] >= dp[len]) { ++len; dp[len] = a[i]; } int p = upper_bound(dp + 1, dp + 1 + len, a[i]) - dp; dp[p] = a[i]; } return len;}void solve(){ scanf("%d %d", &n, &k); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); if (n - 1 <= k) //修改k个必然能全部满足 { printf("%d\n", n); return; } int ans = k + 1; for (int i = 1; i + k - 1 <= n; i++) ans = max(ans, k + LIS(i, i + k - 1)); printf("%d\n", ans);}int main(){ solve(); return 0;}试题 H: 扫描游戏

预计得分10% ~ 30%
暴力思路:
极角排序。之后每次暴力扫描,循环直到扫描不到物品。
总时间复杂度 O ( n 2 ) O(n^2) O(n2)
参考代码:
#include <bits/stdc++.h>using namespace std;const int N = 3e5 + 5;const int INF = 0x3f3f3f3f;struct node{ long long x, y, z, id; double theta; bool operator<(const node &tmp) const { return theta < tmp.theta; }};vector<node> vec;int out[N];node tmp;void solve(){ int n; long long L; scanf("%d %lld", &n, &L); for (int i = 1; i <= n; i++) { out[i] = -1; tmp.id = i; scanf("%lld %lld %lld", &tmp.x, &tmp.y, &tmp.z); tmp.theta = atan2(tmp.y, tmp.x); vec.push_back(tmp); } sort(vec.begin(), vec.end()); int len = (int)vec.size(); int p = -1; for (int i = len - 1; i >= 0; i--) { if (vec[i].x >= 0) { p = i; break; } } if (p == -1) { for (int i = len - 1; i >= 0; i--) { if (vec[i].y <= 0) { p = i; break; } } } if (p == -1) p = (int)vec.size() - 1; vector<node> tmp = vec; vec.clear(); for (int i = p; i >= 0; i--) vec.push_back(tmp[i]); for (int i = (int)tmp.size() - 1; i > p; i--) vec.push_back(tmp[i]); int rk = 0, sum = 0; node pre; pre.theta = INF; while (1) { vector<node> now; int m = vec.size(); for (int i = 0; i < m; i++) if (vec[i].x != INF) now.push_back(vec[i]); m = now.size(); bool flag = 0; for (int i = 0; i < m; i++) { if (L * L >= now[i].x * now[i].x + now[i].y * now[i].y) { L += now[i].z; now[i].x = INF; //标记 flag = 1; if (fabs(now[i].theta - pre.theta) <= 1e-6) out[now[i].id] = rk; else { rk = sum + 1; out[now[i].id] = rk; } sum++; pre = now[i]; } } if (!flag) break; vec = now; } for (int i = 1; i <= n; i++) printf("%d%c", out[i], i == n ? '\n' : ' ');}int main(){ solve(); return 0;}试题 I: 数的拆分

预计得分10%
暴力思路:筛出所有质因子,不能有出现次数只有一次的质因子,并且最多有两个出现次数为奇数次的质因子(出现偶数次只需均分给 x 1 x_1 x1和 y 1 y_1 y1)
总时间复杂度 O ( t s q r t ( n ) ) O(tsqrt(n)) O(tsqrt(n))
参考代码:
#include <bits/stdc++.h>using namespace std;bool check(long long x){ map<int, int> mp; for (int i = 2; i * i <= x; i++) { if (x % i == 0) while (x % i == 0) { x /= i; mp[i]++; } } if (x >= 2) mp[x]++; int odd = 0, flag = 0; for (auto it : mp) { if (it.second == 1) return 0; if (it.second & 1) odd++; if (it.second >= 2) flag = 1; } return odd <= 2;}void solve(){ int t; scanf("%d", &t); while (t--) { long long x; scanf("%lld", &x); puts(check(x) ? "yes" : "no"); }}int main(){ solve(); return 0;}试题 J: 推导部分和

暂时不会。