文章目录

一、 二叉搜索树1.1 概念1.2 操作1.3 代码实现 二、二叉搜索树的应用K模型和KV模型 三、二叉搜索树的性能分析四、AVL树4.1 AVL树的概念4.2 AVL树的实现原理4.3 旋转4.4 AVL树最终代码

---

一、 二叉搜索树

1.1 概念

二叉搜索树（ Binary Search Tree，BST ）是一种特殊的二叉树，它可以是空树，也可以是满足以下性质的一颗二叉树：

若左子树不为空，左子树中所有节点的键值都小于根节点的值。若右子树不为空，右子树中所有节点的键值都大于根节点的值。左右子树也分别为二叉搜索树。

因此，二叉搜索树的中序遍历结果是一个有序序列。这个特性使得二叉搜索树在搜索、插入和删除操作时具有高效性能。

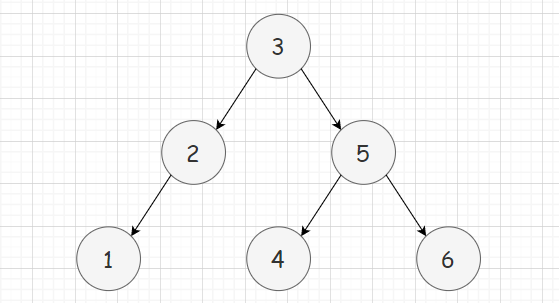
?二叉搜索树的结构示意图

---

1.2 操作

⭕ 对如下二叉搜索树进行操作

查询

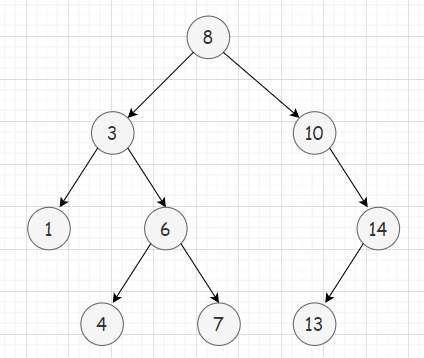
?假设要查询key值是否存在于二叉树中

从根节点开始，key比当前节点的键值大，则往右继续找；key比当前节点的键值小，则往左继续找。若当前节点为空时还没找到，则key值不存在。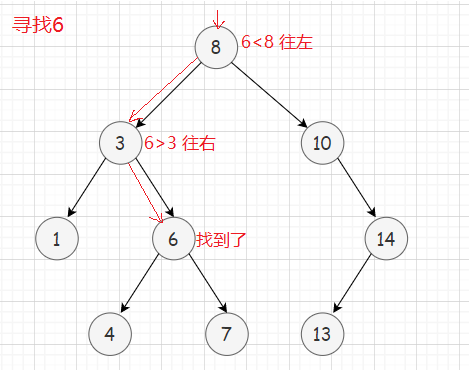

插入

1️⃣若树为空，则直接新增节点，作为该树的根节点
2️⃣若树不为空，则按二叉搜索树查询规则找到插入位置，再建立与父节点的链接关系。

删除

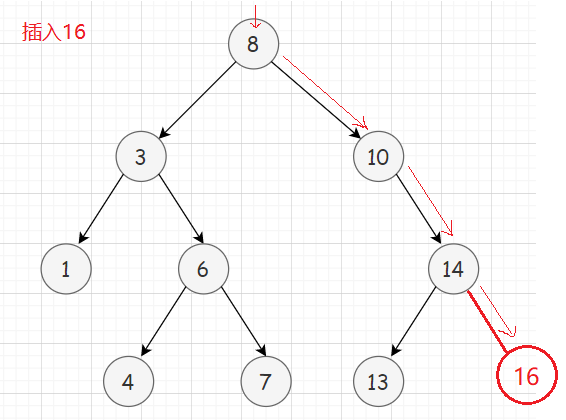
二叉搜索树的删除某个节点后，要想继续保持二叉搜索树的特性，需要进行一些调整。这里分三种情况。

假设将要删除node节点

1️⃣ 若node没有子树，即node为叶子节点，那么直接删除即可。

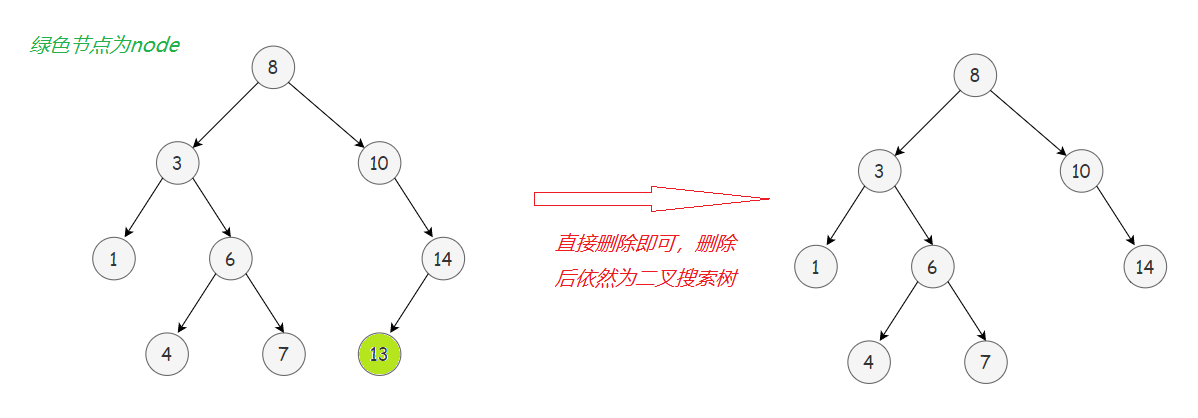
2️⃣ 若node左右子树有一边为空一边非空，则需“托孤”，即把非空一边的子树托付给node父节点。

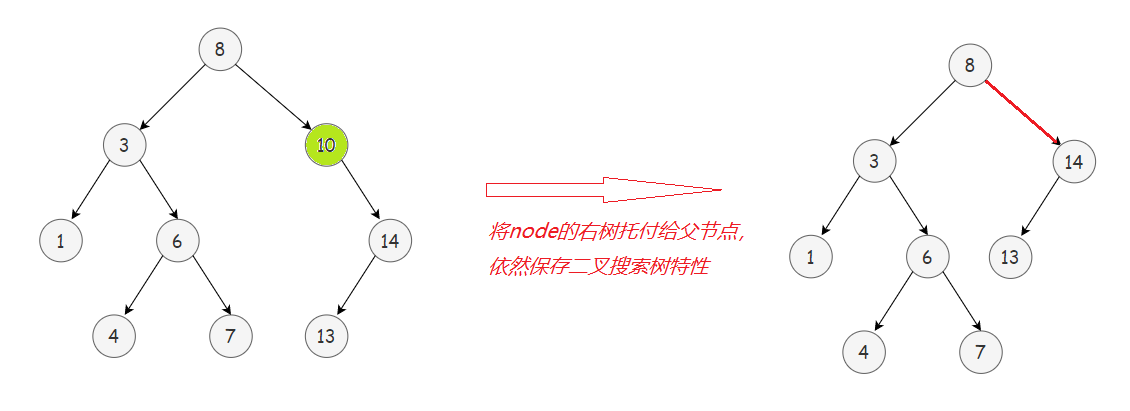
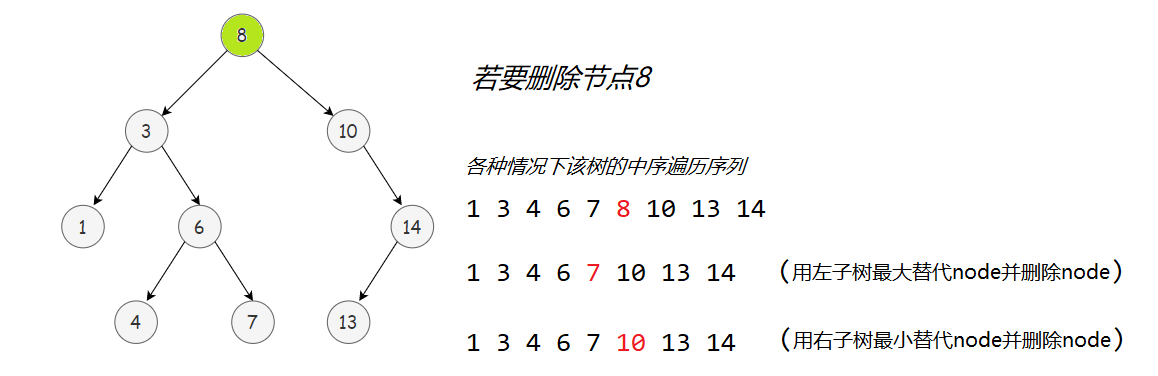
3️⃣ 若node左右子树都存在，则需在左子树中找到最大节点（或在右子树中找到最小节点）来替代node，然后在左子树（或右子树）中删除node。

观察二叉搜索树的中序遍历序列，可见进行上述操作后，中序遍历序列依然有序，二叉搜索树保持其特性。

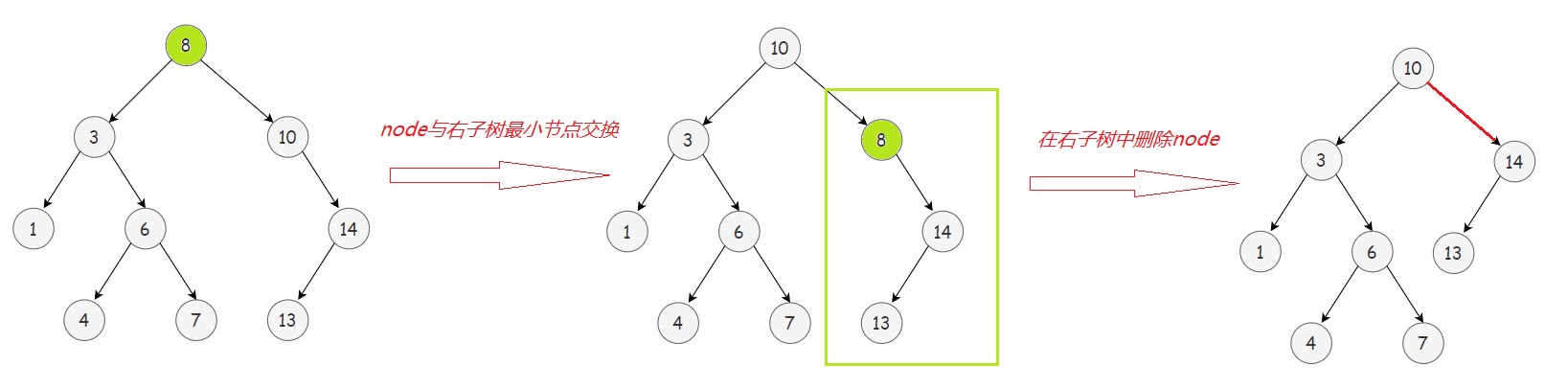
?替换node后，在左子树（或右子树）中删除node，这样做还有一个好处：

因为node是与左子树中最大节点（或右子树中最小节点）替换后，所以替换后的node一定没有右子树（或左子树），因此在这种情况下删除node，必然是删除节点的1️⃣或2️⃣情况，避免了重复3️⃣情况删除而进入死循环。

---

1.3 代码实现

#include <iostream>#include <algorithm>using namespace std;// 二叉搜索树的节点template <class K>struct BSTreeNode{typedef BSTreeNode<K> Self;Self* _pleft;Self* _pright;K _key;BSTreeNode(const K& key):_key(key),_pleft(nullptr),_pright(nullptr){}};// 二叉搜索树template <class K>class BSTree{typedef BSTreeNode<K> Node;typedef BSTreeNode<K>* pNode;public:// constructorBSTree():_root(nullptr){}// destructor~BSTree(){_destroy(_root);}// 中序遍历void Inorder(){_inorder(_root);cout << endl;}// 插入bool Insert(const K& key){// 空树if(_root == nullptr){_root = new Node(key);return true;}// 不为空树，要先找到插入位置else{pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else{return false;}}cur = new Node(key);if (cur->_key > parent->_key)parent->_pright = cur;elseparent->_pleft = cur;return true;}}// 删除void Erase(const K& key){_erase(_root, key);}private:pNode _root;void _inorder(pNode root){if (root == nullptr)return;_inorder(root->_pleft);cout << root->_key << " ";_inorder(root->_pright);}void _destroy(pNode root){if (root == nullptr)return;_destroy(root->_pleft);_destroy(root->_pright);delete root;}bool _erase(pNode& root, const K& key){// 先找到key值的节点pNode cur = root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else // 相等，找到了break;}if (cur == nullptr) // 查无key值节点return false;// 1. cur左右至少有一个空（1️⃣、2️⃣情况）if (cur->_pleft == nullptr || cur->_pright == nullptr){pNode child = cur->_pleft;if (child == nullptr)child = cur->_pright;// cur为根if (cur == root){root = child;}// cur不为根else{if (cur == parent->_pleft){parent->_pleft = child;}else{parent->_pright = child;}}delete cur;cur = nullptr;}// 2. cur左右都非空（3️⃣情况）else{//(1)找到右边最小(也可以是左边最大，通常小的离根较近，我们选用右边最小)的节点代替curpNode minRight = cur->_pright;while (minRight->_pleft){minRight = minRight->_pleft;}swap(cur->_key, minRight->_key);//(2)转换为在cur的右子树删除minRight节点_erase(cur->_pright, minRight->_key); // 此时一定是1️⃣或2️⃣情况}return true;}};

? _erase函数root参数设为引用的妙处在cur为根时，体现为以下两种情况相同处理

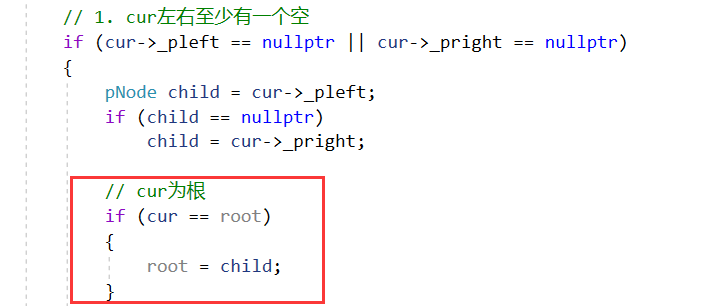
1. _erase(_root, key);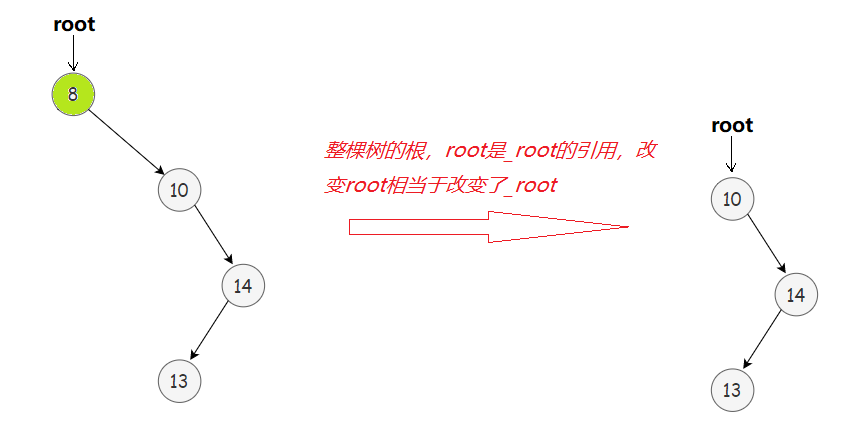

2. _erase(cur->_pright(或cur->_pleft), minRight->_key);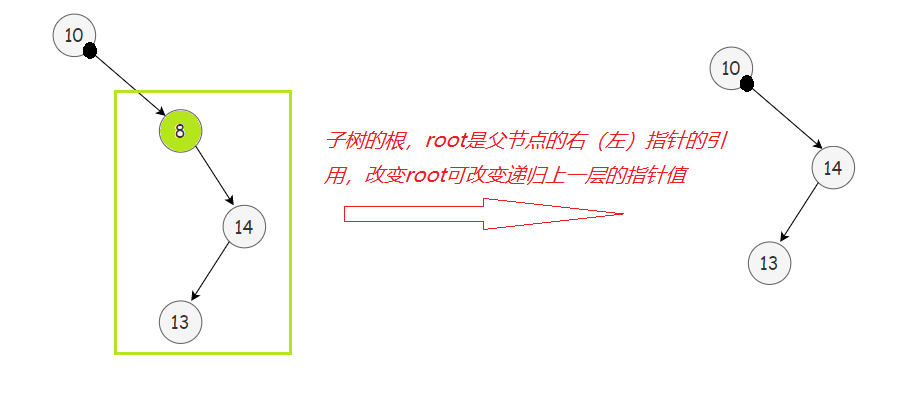

---

二、二叉搜索树的应用

K模型和KV模型

K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到
的值。

比如：给一个单词word，判断该单词是否拼写正确，具体方式如下： 以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树，在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方
式在现实生活中非常常见

比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英 文单词与其对应的中文<word, chinese>就构成一种键值对；
再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出现次数就是<word, count>就构成一种键值对。

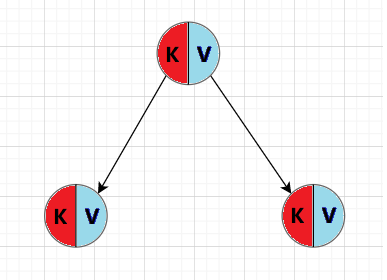
?KV模型的代码实现:

// KV型template <class K, class V>struct BSTreeNode{typedef BSTreeNode<K, V> Self;Self* _pleft;Self* _pright;K _key;V _val;BSTreeNode(const K& key, const V& val): _key(key), _val(val), _pleft(nullptr), _pright(nullptr){}};template <class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;typedef BSTreeNode<K, V>* pNode;public://constructorBSTree():_root(nullptr){}//destructor~BSTree(){_destroy(_root);}void Inorder(){_inorder(_root);cout << endl;}bool Insert(const K& key,const V& val){// 空树if (_root == nullptr){_root = new Node(key, val);return true;}// 不为空树，要先找到插入位置else{pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else{return false;}}cur = new Node(key, val);if (cur->_key > parent->_key)parent->_pright = cur;elseparent->_pleft = cur;return true;}}void Erase(const K& key){_erase(_root, key);}pNode Find(const K& key){pNode cur = _root;while (cur){if (key > cur->_key){cur = cur->_pright;}else if (key < cur->_key){cur = cur->_pleft;}else{return cur;}}return nullptr;}private:pNode _root;void _inorder(pNode root){if (root == nullptr)return;_inorder(root->_pleft);cout << root->_key << ":" << root->_val << endl;_inorder(root->_pright);}void _destroy(pNode root){if (root == nullptr)return;_destroy(root->_pleft);_destroy(root->_pright);delete root;}bool _erase(pNode& root, const K& key){// 先找到key值的节点pNode cur = root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else // 相等，找到了break; }if (cur == nullptr) // 查无key值节点return false;// 1. cur左右至少有一个空if (cur->_pleft == nullptr || cur->_pright == nullptr){pNode child = cur->_pleft;if (child == nullptr)child = cur->_pright;// cur为根if (cur == root){root = child;}// cur不为根else{// cur左右都为空if (child == nullptr){if (parent->_pleft->_key == cur->_key){parent->_pleft = nullptr;}else{parent->_pright = nullptr;}}// cur左右只有一个为空，不为空的为childelse{if (child->_key < parent->_key){parent->_pleft = child;}else{parent->_pright = child;}}if (cur == parent->_pleft){parent->_pleft = child;}else{parent->_pright = child;}}delete cur;cur = nullptr;}//2. cur左右都非空else{//找到右边最小的节点代替curpNode minRight = cur->_pright;while (minRight->_pleft){minRight = minRight->_pleft;}swap(cur->_key, minRight->_key);//转换为在cur的右子树删除minRight节点_erase(cur->_pright, minRight->_key);}return true;}};

---

三、二叉搜索树的性能分析

? 二叉搜索树的插入、删除等操作，时间大部分都花费在查找节点上了。因此分析二叉搜索树的性能，主要看查找的性能。

假设二叉树有N个节点

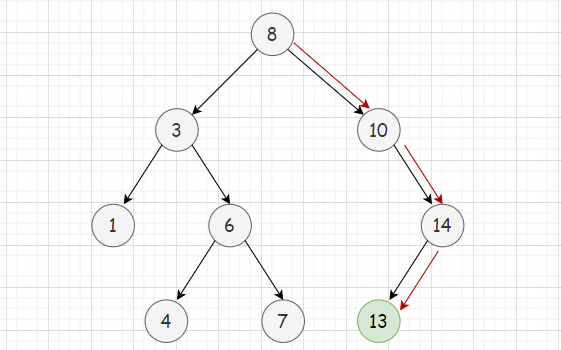
如图是最优情况下的查找，该二叉搜索树接近完全二叉树，此时查找节点的时间复杂度是O(logN)

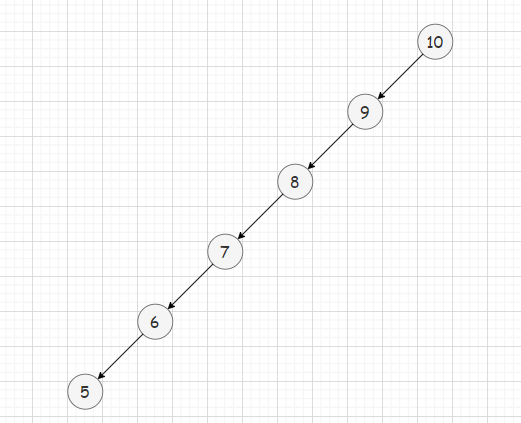
❗但也有上图所示的极端情况，有序插入节点后，二叉搜索树退化为单支，这种情况是最差情况，查找节点的时间复杂度为O(N)

? 二叉搜索树退化为接近单支树时，其效率和性能就失去了。为了解决这个问题，使二叉搜索树始终保持最优情况，我们可以将二叉搜索树改造为AVL树和红黑树。下文分析AVL树。

---

四、AVL树

4.1 AVL树的概念

?二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：
当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

能满足这种特性的树称为AVL树

⭕一颗AVL树可以是一棵空树，也可以是有以下性质的一棵二叉搜索树：

它的左右子树都是AVL树左右子树高度差（简称平衡因子）的绝对值不超过1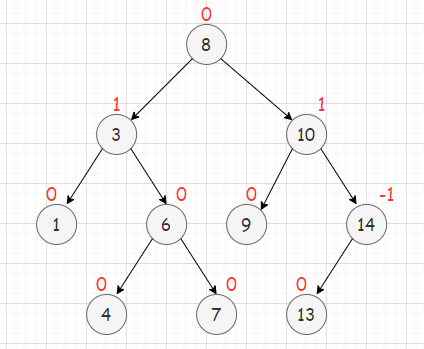

AVL树是一棵高度平衡的树。一棵n个节点的AVL树的高度为O(logn)，查找的时间复杂度为O(logn)。

⭕定义

// AVL树的节点template <class T>struct AVLTreeNode{AVLTreeNode(const T& val):_val(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}AVLTreeNode* _left; // 左指针AVLTreeNode* _right; // 右指针AVLTreeNode* _parent; // 双亲指针T _val;int _bf;// 平衡因子};

// AVL树template <class T>class AVLTree{typedef AVLTreeNode<T> node;typedef AVLTreeNode<T>* ptr;public:AVLTree():_root(nullptr){}bool insert(const T& val);private:ptr _root;};

---

4.2 AVL树的实现原理

?AVL树的原理主要体现在插入时要通过对节点的调节，以保证每个节点的左右子树高度差绝对值不超过1（即平衡因子不超过1）。插入后，分为以下三种情况。

默认平衡因子 = 右子树高度 - 左子树高度

插入后，父节点的平衡因子变为0

插入后，父节点的平衡因子变为1或-1

插入后，父节点的平衡因子变为2或-2

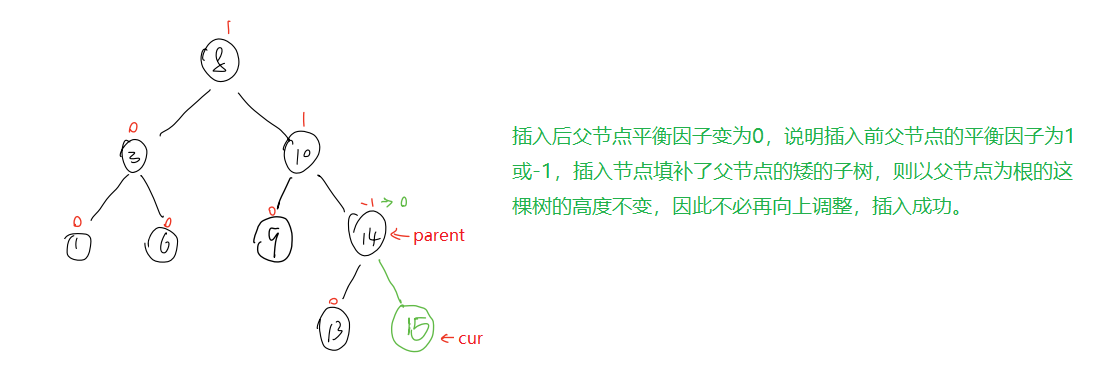
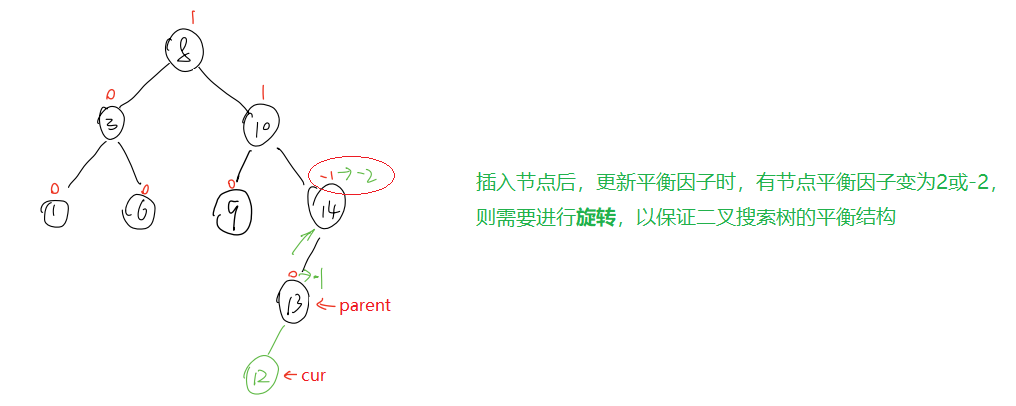
那么这里的旋转到底是怎么一回事？见后文详细分析。

? 先搭建AVL树insert插入函数定义的大致框架

bool insert(const T& val){// 先按二叉搜索树规则，找到插入位置ptr cur = _root;ptr parent = nullptr;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{// 相同元素不能插入return false;}}// 创建新节点并插入cur = new node(val);// 若根为空，直接把cur作根if (_root == nullptr){_root = cur;return true;}else{if (cur->_val < parent->_val){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}}// 更新平衡因子while (parent){if (cur == parent->_left){(parent->_bf)--;}else{(parent->_bf)++;}// 1.parent的_bf更新后为0if (parent->_bf == 0){// 插入成功break;}// 2.parent的_bf更新后为1或-1，此时需要继续向上更新平衡因子else if (parent->_bf == 1 || parent->_bf == -1){//持续往上更新cur = parent;parent = parent->_parent;}// 3.parent的_bf更新后为2或-2，此时需要旋转，旋转后以parent为根的子树为平衡二叉树，不需要在继续向上更新平衡因子else if (parent->_bf == 2 || parent->_bf == -2){// 旋转...break;}}return true;}

4.3 旋转

?如果在一棵原本是平衡的AVL树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。这种调整称之为旋转。根据节点插入位置的不同，AVL树的旋转分为四种：

左左 —— 右单旋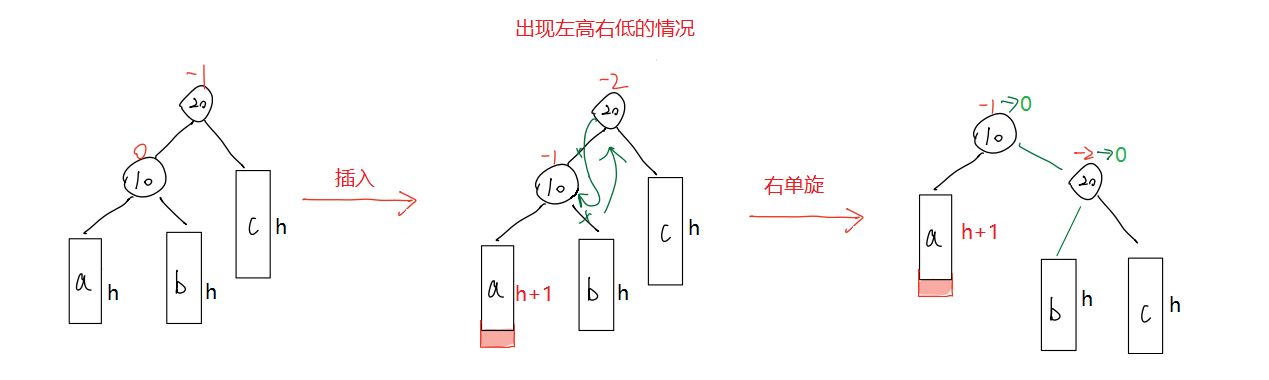

为什么能这样旋转？

b在20的左子树，肯定比20小，故能作20的左子树20和b都大于10，故以20为根的子树能作10的右子树

? 代码实现

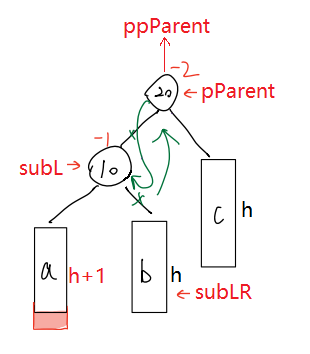
// 左左--右单旋void RotateR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;ptr ppParent = pParent->_parent;//建立新的链接关系//1.pParent(父)和subLR(子)pParent->_left = subLR;if (subLR)subLR->_parent = pParent;//2.subL(父)和pParent(子)subL->_right = pParent;pParent->_parent = subL;//3.ppParent(父)和subL(子)if (pParent == _root){_root = subL;}else{if (ppParent->_left == pParent){ppParent->_left = subL;}else{ppParent->_right = subL;}}subL->_parent = ppParent;//4.更新平衡因子subL->_bf = pParent->_bf = 0;}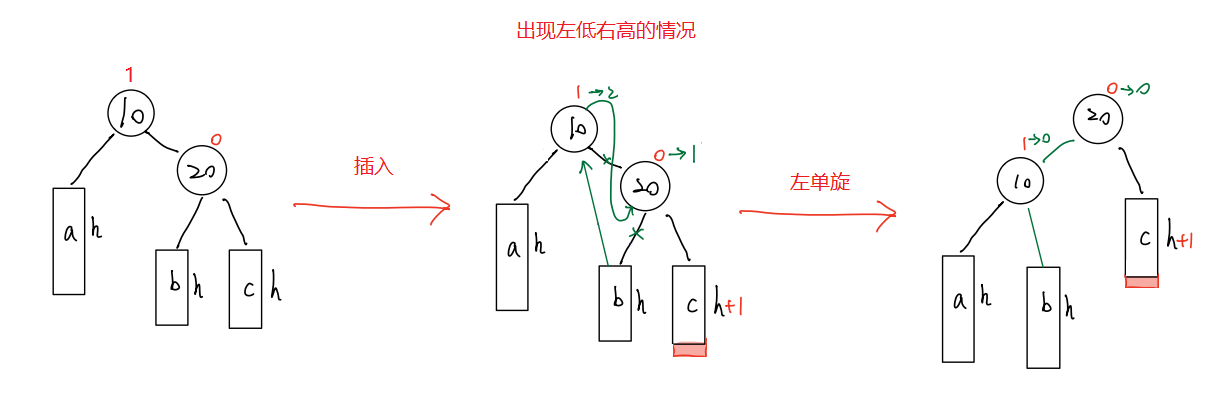

右右 —— 左单旋

? 代码实现

// 右右--左单旋void RotateL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;ptr ppParent = pParent->_parent;pParent->_right = subRL;if (subRL)subRL->_parent = pParent;subR->_left = pParent;pParent->_parent = subR;if (pParent == _root){_root = subR;}else{// 是否可以用函数参数引用 ptr& pParent 优化？//if (subR->_val < ppParent->_val)if (ppParent->_left == pParent){ppParent->_left = subR;}else{ppParent->_right = subR;}}subR->_parent = ppParent;subR->_bf = pParent->_bf = 0;}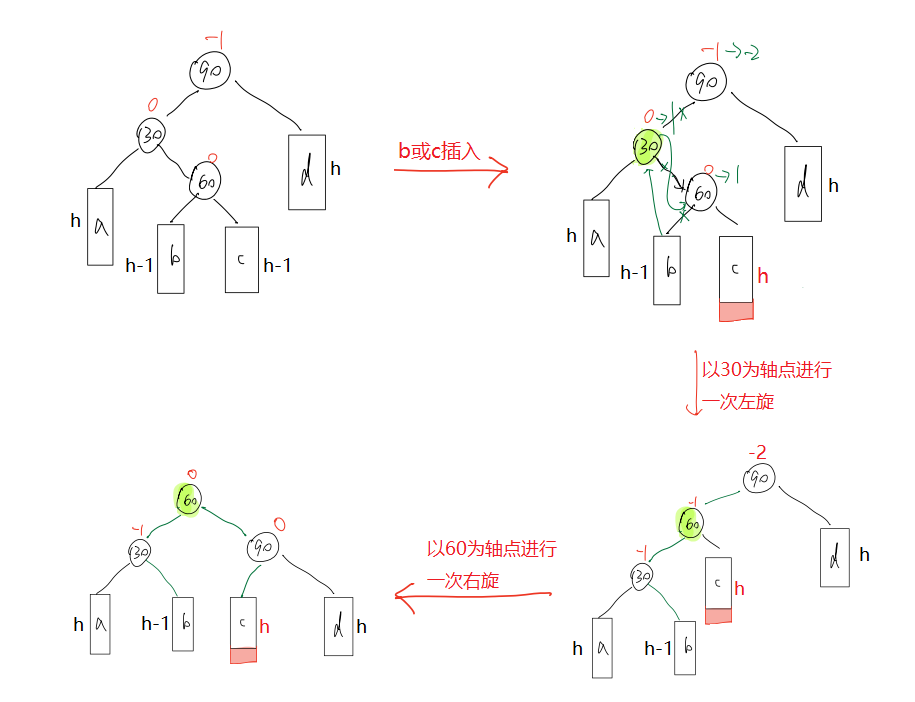

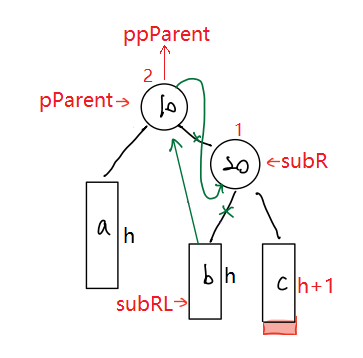
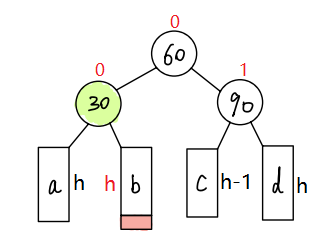
左右 —— 左右双旋

?我们可以复用RotateL（左单旋）和RotateR（右单旋）来实现右左双旋，但需要注意的是，这两个函数会把平衡因子直接更新为0，但是观察右左双旋的过程图，发现结果所更新节点的平衡因子不全为0。因此，右左双旋要自己更新平衡因子，不能依赖于RotateL和RotateR。

当在c子树插入新节点时，旋转后的结果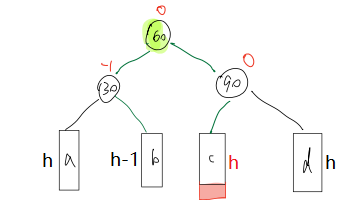

当在b子树插入新节点时，旋转后的结果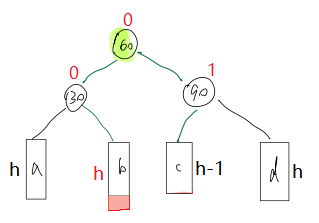

特殊情况，当h==0时，30的右子树为空，60就是新插入节点。最终平衡因子全为0。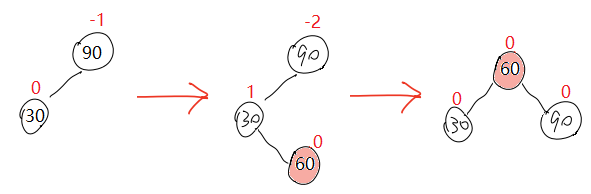

? 代码实现

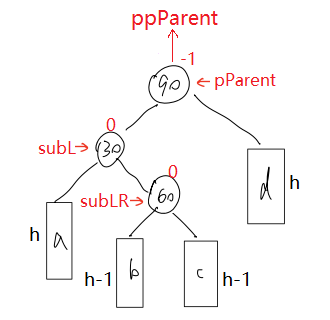
?通过上两张图可以发现，当在c子树插入时，最终subL指向节点的平衡因子为-1，其他两个为0；当在b子树插入时，最终pParent指向节点的平衡因子为1，其他两个为0。因此，判断在哪颗树插入时决定最终如何更新平衡因子的关键，而插入后且调整前的subLR的平衡因子就可以判断。插入后且调整前，若subLR的平衡因子为1，则是在c子树插入；若subLR的平衡因子为-1，则是在b子树插入。还有h==0的特殊情况，此时subLR的平衡因子为0，作特殊处理。

void RotateLR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;int bf = subLR->_bf; // 保存插入后调整前subLR的平衡因子// 两次旋转RotateL(subL);RotateR(pParent);// 更新平衡因子if (bf == 1){subLR->_bf = 0;subL->_bf = -1;pParent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 1;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 0;}else{assert(false);}}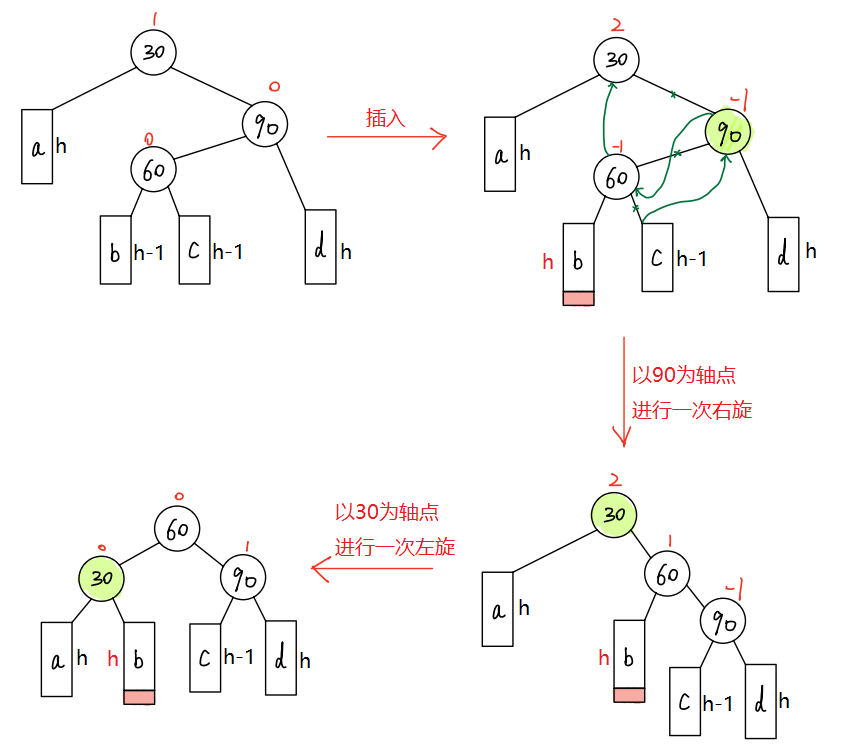

右左 —— 右左双旋
当在c子树插入新节点时，旋转后的结果

当在b子树插入新节点时，旋转后的结果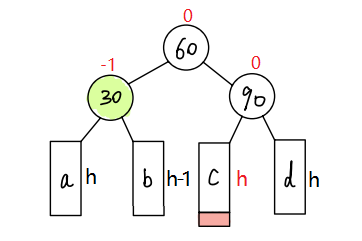

?代码实现

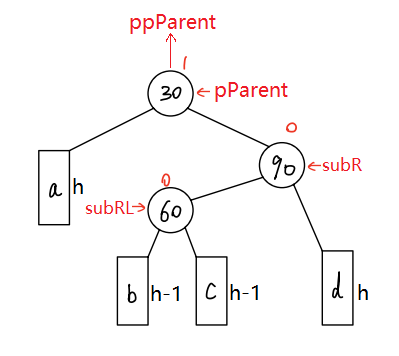
void RotateRL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(pParent);if (bf == 1){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;pParent->_bf = 0;}else if (bf == 0){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = 0;}else{assert(false);}}

4.4 AVL树最终代码

// AVL树的节点template <class T>struct AVLTreeNode{AVLTreeNode(const T& val):_val(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;T _val;int _bf;// 平衡因子};// AVL树template <class T>class AVLTree{typedef AVLTreeNode<T> node;typedef AVLTreeNode<T>* ptr;public:// 构造函数AVLTree():_root(nullptr){}// 析构函数~AVLTree(){destroy(_root);}// 中序遍历void InOrder(){_inorder(_root);}// 插入新节点bool insert(const T& val){// 先按二叉搜索树规则，找到插入位置ptr cur = _root;ptr parent = nullptr;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{// 相同元素不能插入return false;}}// 创建新节点并插入cur = new node(val);if (_root == nullptr){_root = cur;return true;}else{if (cur->_val < parent->_val){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}}// 更新平衡因子while (parent){if (cur == parent->_left){(parent->_bf)--;}else{(parent->_bf)++;}// 1.parent的_bf更新后为0if (parent->_bf == 0){// 插入成功break;}// 2.parent的_bf更新后为1或-1，此时需要继续向上更新平衡因子else if (parent->_bf == 1 || parent->_bf == -1){//持续往上更新cur = parent;parent = parent->_parent;}// 3.parent的_bf更新后为2或-2，此时需要旋转，旋转后以parent为根的子树为平衡二叉树，不需要在继续向上更新平衡因子else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}}return true;}bool IsBalance()  {return is_balance(_root);}int Height(){return get_height(_root);}private:// 检查该树是否平衡bool is_balance(ptr root){if (root == nullptr)return true;int leftHeight = get_height(root->_left);int rightHeight = get_height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_val << "平衡因子异常" << endl;}return (abs(rightHeight - leftHeight) == 1 || rightHeight == leftHeight)&& is_balance(root->_left)&& is_balance(root->_right);}// 获取以root为根的子树的高度int get_height(ptr root){if (root == nullptr)return 0;return 1 + max(get_height(root->_left), get_height(root->_right));}// 析构函数的子函数void destroy(ptr root){if (root == nullptr)return;destroy(root->_left);destroy(root->_right);delete root;}void _inorder(ptr root){if (root == nullptr)return;_inorder(root->_left);cout << root->_val << " ";_inorder(root->_right);}// 左左--右单旋void RotateR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;ptr ppParent = pParent->_parent;//1.pParent(父)和subLR(子)pParent->_left = subLR;if (subLR)subLR->_parent = pParent;//2.subL(父)和pParent(子)subL->_right = pParent;pParent->_parent = subL;//3.ppParent(父)和subL(子)if (pParent == _root){_root = subL;}else{// 是否可以用函数参数引用 ptr& pParent 优化？if (ppParent->_left == pParent){ppParent->_left = subL;}else{ppParent->_right = subL;}}subL->_parent = ppParent;//4.更新平衡因子subL->_bf = pParent->_bf = 0;}// 右右--左单旋void RotateL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;ptr ppParent = pParent->_parent;pParent->_right = subRL;if (subRL)subRL->_parent = pParent;subR->_left = pParent;pParent->_parent = subR;if (pParent == _root){_root = subR;}else{// 是否可以用函数参数引用 ptr& pParent 优化？//if (subR->_val < ppParent->_val)if (ppParent->_left == pParent){ppParent->_left = subR;}else{ppParent->_right = subR;}}subR->_parent = ppParent;subR->_bf = pParent->_bf = 0;}void RotateLR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(pParent);if (bf == 1){subLR->_bf = 0;subL->_bf = -1;pParent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 1;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 0;}else{assert(false);}}void RotateRL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(pParent);if (bf == 1){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;pParent->_bf = 0;}else if (bf == 0){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = 0;}else{assert(false);}}ptr _root;};

完。