问题背景
西西艾弗岛荒野求生大赛还有 n 天开幕！
问题描述
为了在大赛中取得好成绩，顿顿准备在 n 天时间内完成“短跑”、“高中物理”以及“核裂变技术”等总共 m 项科目的加强训练。其中第 i 项（1≤i≤m）科目编号为 i，也可简称为科目 i。已知科目 i 耗时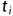 
天，即如果从第 a 天开始训练科目 i，那么第 
天就是该项训练的最后一天。
大部分科目的训练可以同时进行，即顿顿在同一天内可以同时进行多项科目的训练，但部分科目之间也存在着依赖关系。如果科目 i 依赖科目 j，那么只能在后者训练结束后，科目 i 才能开始训练。具体来说，如果科目 j 从第 a 天训练到第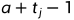 
天，那么科目 i 最早只能从第 
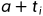天开始训练。还好，顿顿需要训练的 m 项科目依赖关系并不复杂，每项科目最多只依赖一项别的科目，且满足依赖科目的编号小于自己。那些没有任何依赖的科目，则可以从第 1 天就开始训练。
对于每一项科目，试计算：
1）最早开始时间：该科目最早可以于哪一天开始训练？
2）最晚开始时间：在不耽误参赛的前提下（n 天内完成所有训练），该科目最晚可以从哪一天开始训练？
n 天内完成所有训练，即每一项科目训练的最后一天都要满足 ≤n。需要注意，顿顿如果不能在 n 天内完成全部 m 项科目的训练，就无法参加大赛。这种情况下也就不需要再计算“最晚开始时间”了。
输入格式
从标准输入读入数据。
输入共三行。
输入的第一行包含空格分隔的两个正整数 n 和 m，分别表示距离大赛开幕的天数和训练科目的数量。
输入的第二行包含空格分隔的 m 个整数，其中第 i 个（1≤i≤m）整数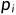 
表示科目 i 依赖的科目编号，满足 0≤
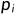<i；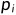
=0 表示科目 i 无依赖。
输入的第三行包含空格分隔的 m 个正整数，其中第 i 个（1≤i≤m）数 
表示训练科目 i 所需天数，满足 1≤
≤n。
输出格式
输出到标准输出中。
输出共一行或两行。
输出的第一行包含空格分隔的 m 个正整数，依次表示每项科目的最早开始时间。
如果顿顿可以在 n 天内完成全部 m 项科目的训练，则继续输出第二行，否则输出到此为止。
输出的第二行包含空格分隔的 m 个正整数，依次表示每项科目的最晚开始时间。
样例 1
输入
10 50 0 0 0 01 2 3 2 10输出
1 1 1 1 110 9 8 9 1说明
五项科目间没有依赖关系，都可以从第 1 天就开始训练。
10 天时间恰好可以完成所有科目的训练。其中科目 1 耗时仅 1 天，所以最晚可以拖延到第 10 天再开始训练；而科目 5 耗时 10 天，必须从第 1 天就开始训练。
样例 2
输入
10 70 1 0 3 2 3 02 1 6 3 10 4 3输出
1 3 1 7 4 7 1说明
七项科目间的依赖关系如图所示，其中仅科目 5 无法在 10 天内完成训练。
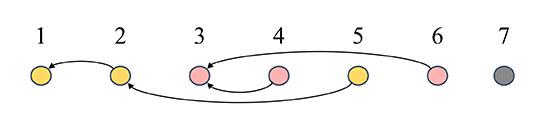
具体来说，科目 5 依赖科目 2、科目 2 又依赖于科目 1，因此科目 5 最早可以从第 4 天开始训练。
样例 3
输入
10 50 1 2 3 410 10 10 10 10输出
1 11 21 31 41子任务
70% 的测试数据满足：顿顿无法在 n 天内完成全部 m 项科目的训练，此时仅需输出一行“最早开始时间”；
全部的测试数据满足 0<n≤365 且 0<m≤100。
思路
最早开始时间和依赖关系有关，若某科目无依赖（即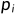
=0 ），则第一天就可以开始；若科目i依赖于科目j，且科目j无依赖，则科目i等科目j做完即可开始；若科目j也依赖于科目k，则科目i要等科目k，科目j做完才开始，以此类推......
for (int i = 1; i <= m; i++) { if (p[i] == 0) cout << 1 << " "; else { cout << q[p[i]] + 1 << " "; q[i] += q[p[i]] ; } }由题干：70% 的测试数据满足：顿顿无法在 n 天内完成全部 m 项科目的训练，此时仅需输出一行“最早开始时间”可知，得70分只用输出一行--最早开始时间。
70分代码
#include <iostream>using namespace std;int main() { int n, m; cin >> n >> m; int p[105] = {0}; int q[105] = {0}; for (int i = 1; i <= m; i++) { cin >> p[i]; } for (int i = 1; i <= m; i++) { cin >> q[i]; } for (int i = 1; i <= m; i++) { if (p[i] == 0) cout << 1 << " "; else { cout << q[p[i]] + 1 << " "; q[i] += q[p[i]] ; } } return 0;}下面来看100分的思路，加上了最晚开始时间。
假设能在n天内完成所有训练，则最晚开始时间应是自己本身加上后面与自己有依赖关系的训练的时间之和t0，t=n-t0+1.
当然，与自己有依赖的可能不止一个，所以应该是自己与一个有依赖的训练的时间之和的最大值，即为t0，可求得最晚的开始时间。
明白上述后，来判断什么条件下需要输出第二行，我们定义一个判断的bool类型的变量flag，若某训练本身需的时间加上在自身前需优先完成的训练的时间之和大于了n，则说明不能按时完成所以训练，即不输出第二行。
if (q[p[i]] + q[i] > n) flag = 1;q[i] += q[p[i]] ; //多重依赖关系的累加考虑到解决第一个问题改动了q[]数组，故新开一个q1[]数组，来供第二个问题。
若判断得出能完成所以训练，则来求出一组有依赖关系训练所需最大总时间：
从后往前循环，先让r数组加上自己所需时间
判断是否有优先完成的训练（即p[i]是否为0），若不为0，则让前面需优先完成的训练r[p[i]]加上自己的时间r[i]（由于前面的训练可能不止一个依赖关系的训练，故取最大值max）
if (p[i]) r[p[i]] = max(r[i], r[p[i]]);以此反复，越往前，后面的训练对前面的影响就统计进去，前面r数组就考虑了后面有依赖关系的训练，求出了一系列训练的最大总时间。
然后最晚开始时间就是准备时间n减去总时间r[i]加上1，即n-r[i]+1;
100分代码
#include <iostream>#include <cmath>using namespace std;int main() { int n, m; cin >> n >> m; int p[105] = {0}; int q[105] = {0}; int q1[105] = {0}; int r[105] = {0}; bool flag = 0; for (int i = 1; i <= m; i++) { cin >> p[i]; } for (int i = 1; i <= m; i++) { cin >> q[i]; q1[i] = q[i]; } for (int i = 1; i <= m; i++) { if (p[i] == 0) cout << 1 << " "; else { cout << q[p[i]] + 1 << " "; if (q[p[i]] + q[i] > n) flag = 1; q[i] += q[p[i]] ; } } if (!flag) { cout << endl; for (int i = m; i >= 1; i--) { r[i] += q1[i]; if (p[i]) r[p[i]] = max(r[i], r[p[i]]); } for (int i = 1; i <= m; i++) { r[i] = n - r[i] + 1; cout << r[i]<<" "; } } return 0;}结尾
作为CSP第二题难度有些提升，但拿70分还是比较简单的，100分的解法由于实力不济，尚在学习，也想了一久，最后写出了我认为比较简单容易理解的做法，如有问题，还望包涵，欢迎指出。