文章目录

题目

需要知道的异或

首先说一下异或这个小可爱。
异或就是不同的返回1，相同的返回0。
比如：100100^000101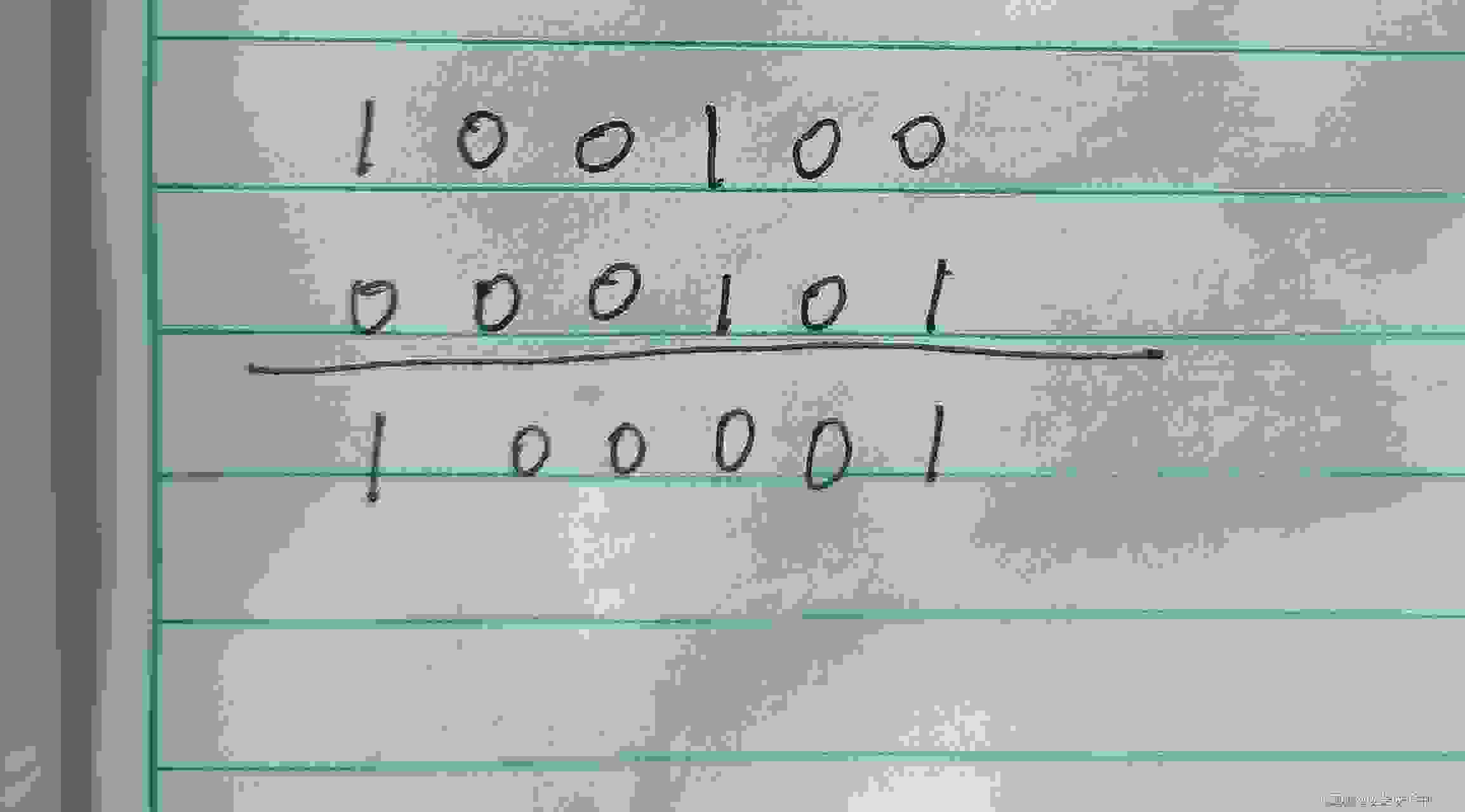

那么很容易得到如果是一个数和它自己异或，得到的铁定是0，（自己和自己的每个二进制位当然是一模一样的），而一个数异或0得到的肯定是它自己，因为二进制0异或0还是得到0，二进制1异或0还是得到1，所以异或0前后没有改变。
另外还有一个结论
如果a^b=x
那么a^x=b
这个结论是解决这道题的关键。推论如下：
∵ a^b=x
∴ a^b^b=x^b
又∵ 一个数异或它自己等于0,一个数异或0等于它自己
∴ a^b^b=a^0=a=x^b
∴ 如果a^b=x,那么a^x=b

解题思路

能否从某个区间 [l,r] 中选择两个数使得他们的异或等于 x ,如果[l,r]的一个子集符合条件，那么[l,r]自然也符合条件。
如果[1,3]存在这样两个数，那么[1,∞）必然也存在这两个数。换句话说，起决定因素的是子集，越小的子集决定度越精准。问题就可以转换为，求以一个数为右端口时最大的区间左端口。

这里很容易想到动态规划，不然会重复很多无用计算，而且它的数据真的庞大地不要脸。。。导致后续还需要一个我以前见都没见过的代码来辅助。。。

那么把每一个数的最大左端口算出来，用dp[r]数组来存它最大的左端口，首先让每一个数与x异或一下，就得到符合条件的数字，。但是有可能它前面有个更小的子集符合条件，所以就要存那个更小子集的左端口。

比如如果d^x=c,b^x=a,那么dp[d的序号]=dp[b的序号]=a的序号,看自己的左端口更大还是前面一个兄弟的左端口更大。

那么思路总结起来就是：
求a^x得到数b，（先假定a>b）那么dp[a的序号]=max(dp[a的序号-1],map[b])
map[b]就是数b的序号。

大概思路也许不难，但是代码难的一批。我最开始用了双重循环，超时超到我爆炸，然后看题解，实在佩服 算法也太难了吧 这位大佬的思路。循环一点都没浪费啊，在输入数据的那个循环被大佬用明白了。我还拘泥于用数组存。上代码吧。大佬的代码，我用我的理解来讲解。

#include<iostream>#include<map>using namespace std;typedef long long ll;const int N=1e5+5;ll n,m,x;int dp[N];    map<ll,int> mp; //输入一个数，就用键值对来存储这个数的序号

ios_base::sync_with_stdio(0);  cin.tie(0);     //加速（很关键！）

c++的cin速度很慢，原理各位自己查，反正加上这两行就快了。
ios是iostream的缩写，base是基础，sync可以用谐音 傻样脑残 来记。

 for(int i=1;i<=n;i++){    ll data;    cin>>data; //输入数据    dp[i]=max(dp[i-1],mp[data^x]);    //mp存放另一个数的序号    mp[data]=i; //存放当前输入数据的序号，要是它能被后面的数异或得到，后面的数就会用到这个i  }

代码

#include<iostream>#include<map>using namespace std;typedef long long ll;const int N=1e5+5;ll n,m,x;int dp[N];    //a^b=x  a,b中早出现的数字位置map<ll,int> mp;int max(int a,int b){  return a>b?a:b;}int main(){  ios_base::sync_with_stdio(0);  cin.tie(0);     //加速（很关键！）  cin>>n>>m>>x;  for(int i=1;i<=n;i++){    ll data;    cin>>data;    dp[i]=max(dp[i-1],mp[data^x]);    //mp存放另一个数的位置    mp[data]=i;  }  while(m--){    int l,r;    cin>>l>>r;    if(dp[r]>=l) cout<<"yes\n";    else cout<<"no\n";  }  return 0;}