目录
01 读取数据
02 赋值变量
03 时间序列值绘制
04 读取包
05 单位根检验,又称平稳性检验
06 自相关图和偏相关图
07 白噪声检验或纯随机性检验
08 模型拟合
09 显著性检验
10 预测未来趋势
结语:
我使用的是:R+Rstudio

01 读取数据
读取数据(read.table),数据位置("F:/笔记/Rstudio/A1_7.csv")

首先找到文件

点击上方文件夹获取文件位置
复制文件位置“F:\笔记\Rstudio”后将“\”改为“/”,在后面加上文件名
改变后:"F:/笔记/Rstudio/A1_7.csv"
sep=","(空格位置用“,”代替)
header=T(数据第一行是标题,不属于数据)
data(将数据赋值给data)
data<-read.table("F:/笔记/Rstudio/A1_7.csv",sep=",",header=T) #data数据02 赋值变量
data$number(取数据data中的名字为number的一列,依据数据具体名称来定,是需要研究的部分)
将提取的一列变量"x"
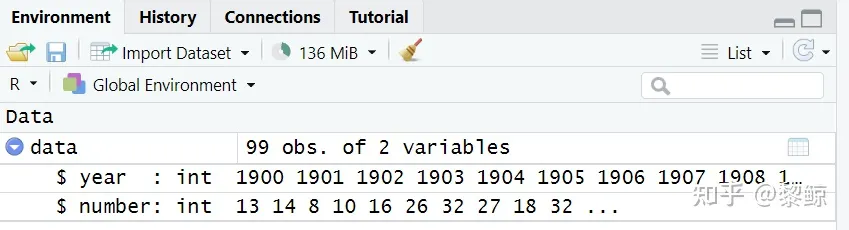
在这个窗口可以看见
x<-ts(data$number,start=1900)#ts时间序列 x时间序列未知量03 时间序列值绘制
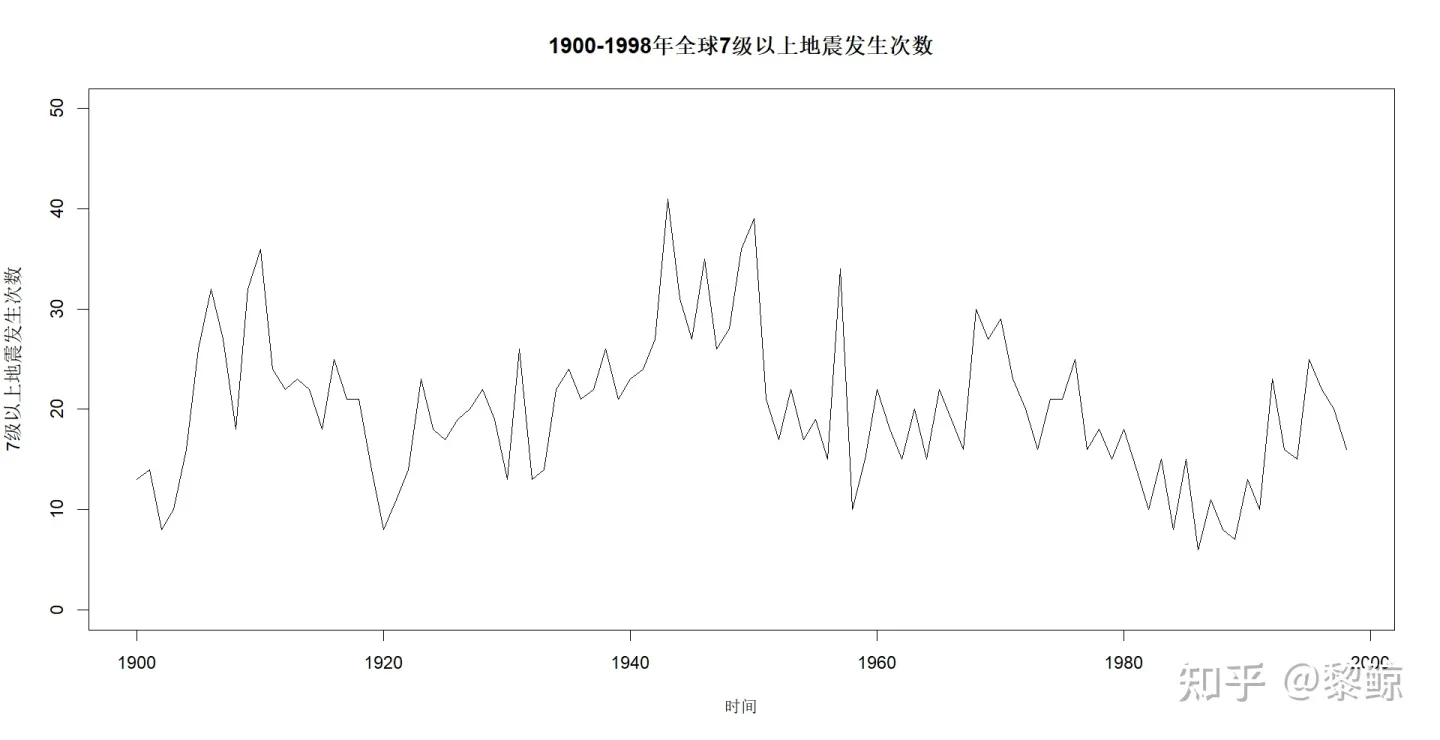
绘制时间序列图用plot()
研究变量为:x
main:主标题
xlab:x轴变量名称
ylab:y轴变量名称
xlim:x轴取值范围
ylim:y轴取值范围
plot( x, main = "1900-1998年全球7级以上地震发生次数", xlab = "时间",ylab="7级以上地震发生次数", xlim = c(1900,1998),ylim=c(0,50))绘图如下:
可以通过col=改变线的颜色,可以是1、2、3、4代表黑、红、绿、蓝,或是直接打出颜色名称
例如:blue,yellow,grey,lavender
根据喜好搭配
pch=节点的形状(从0~25,每个数字对应不同形状)

type参数用来控制所生成散点图的类型,有如下几个选项:
type=“p”表示绘制单独的点
type=“l”表示绘制点连成的折线
type=“b”表示有线连接的点
type=“o”表示将点绘在线上
type=“h”表示从点到x轴的垂线
type=“s”表示阶梯式图
type=“n”表示不绘制图
plot( x, main = "1900-1998年全球7级以上地震发生次数", xlab = "时间",ylab="7级以上地震发生次数", xlim = c(1900,1998),ylim=c(0,50), type="o",pch=24,col=5)
04 读取包
包需要提前下载才可以读取
library(fBasics) #加载包library(fUnitRoots)library(forecast)下载包的流程:
install.packages(fBasics)运行这个代码就可以了,不同包更改括号里的内容即可
05 单位根检验,又称平稳性检验
for(i in 0:1) print( adfTest(x,#adf检验,单位根检验 lag=i, type="nc", title = "7级以上地震发生次数单位根检验"))for(i in 0:3) print( adfTest(x, lag=i, type="c", title = "7级以上地震发生次数单位根检验"))for(i in 0:3) print( adfTest(x, lag=i, type="ct", title = "7级以上地震发生次数单位根检验"))adfTest(x)代码运行结果:
> for(i in 0:1) print(
+ adfTest(x,#adf检验,单位根检验
+ lag=i,
+ type="nc",
+ title = "7级以上地震发生次数单位根检验"))
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 0
STATISTIC:
Dickey-Fuller: -1.5845
P VALUE:
0.1081
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 1
STATISTIC:
Dickey-Fuller: -1.0451
P VALUE:
0.28
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
> for(i in 0:3) print(
+ adfTest(x,
+ lag=i,
+ type="c",
+ title = "7级以上地震发生次数单位根检验"))
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 0
STATISTIC:
Dickey-Fuller: -5.354
P VALUE:
0.01
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 1
STATISTIC:
Dickey-Fuller: -3.9179
P VALUE:
0.01
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 2
STATISTIC:
Dickey-Fuller: -3.1832
P VALUE:
0.02451
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 3
STATISTIC:
Dickey-Fuller: -2.9558
P VALUE:
0.04427
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Warning messages:
1: In adfTest(x, lag = i, type = "c", title = "7级以上地震发生次数单位根检验") :
p-value smaller than printed p-value
2: In adfTest(x, lag = i, type = "c", title = "7级以上地震发生次数单位根检验") :
p-value smaller than printed p-value
> for(i in 0:3) print(
+ adfTest(x,
+ lag=i,
+ type="ct",
+ title = "7级以上地震发生次数单位根检验"))
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 0
STATISTIC:
Dickey-Fuller: -5.5514
P VALUE:
0.01
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 1
STATISTIC:
Dickey-Fuller: -4.1418
P VALUE:
0.01
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 2
STATISTIC:
Dickey-Fuller: -3.5099
P VALUE:
0.04484
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Title:
7级以上地震发生次数单位根检验
Test Results:
PARAMETER:
Lag Order: 3
STATISTIC:
Dickey-Fuller: -3.3716
P VALUE:
0.06336
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
Warning messages:
1: In adfTest(x, lag = i, type = "ct", title = "7级以上地震发生次数单位根检验") :
p-value smaller than printed p-value
2: In adfTest(x, lag = i, type = "ct", title = "7级以上地震发生次数单位根检验") :
p-value smaller than printed p-value
> adfTest(x)
Title:
Augmented Dickey-Fuller Test
Test Results:
PARAMETER:
Lag Order: 1
STATISTIC:
Dickey-Fuller: -1.0451
P VALUE:
0.28
Description:
Mon Jan 9 15:40:36 2023 by user: Lenovo
从代码运行结果里找PVALUE的数值,数值大于0.05就是拒绝原假设,单位根不存在,序列平稳。
06 自相关图和偏相关图
par(mfrow=c(2,1))#分画布2行1列acf(x) #自相关pacf(x) #偏自相关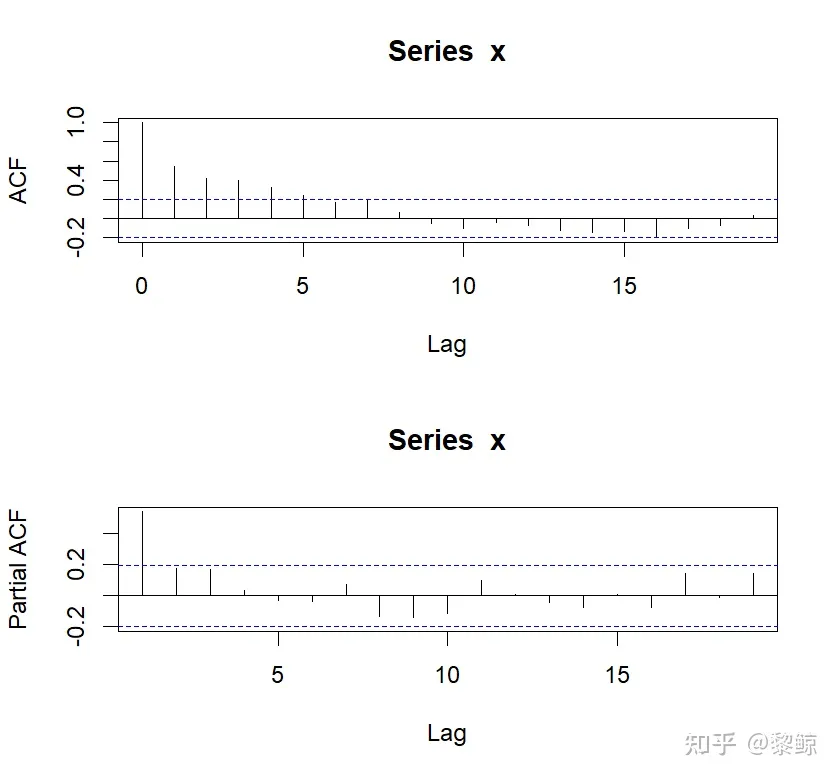
acf自相关(上) pacf偏自相关(下)
观察两图,发现自相关拖尾,偏自相关1阶截尾,预测模型为AR模型
07 白噪声检验或纯随机性检验
for(k in 1:2) print( #白噪声检验,分析前后各一次 Box.test(x, lag=6*k, #type和l等价 type="Ljung-Box")) #服从卡方分布#x-squared为卡方分布值,查表的值#df为卡方检验自由度#p-value 为p值#若想显著性检验,检验目标为残差,验证残差是否为白噪声,为白噪声好代码运行结果:

观察p-value的值,两值均小于0.05,拒绝原假设,序列非白噪声,序列有继续研究的价值。
08 模型拟合
x.fit<-arima(x,order=c(1,0,0),m="ML");x.fit#平稳序列模型运行结果:

图1
根据自相关拖尾,偏相关1阶截尾,模拟AR(1)
x.fit适合x的一个模型
ML为最大似然估计法 ,CSS条件最小估计法 ,ML-CSS两种混合法
中间位置0固定 (差分),若是MA(1)则c(0,0,1)
arima(x=序列x,)
Coefficients系数
ar1,模型AR系数
intercept截距miu
Xt的一个公式
s.e.估计量的标准差
sigma^2 estimated as 某某的估计是
log likelihood 极大似然对数值
aic最小信息准则,越小越好(多个模型间的比较)
09 显著性检验
re<-x.fit$residuals #残差refor(k in 1:2) print( Box.test(re, #残差 lag=6*k, type="Ljung-Box")) qt(0.975,97)t1=0.5432/0.0840;t1t2=19.8911/1.3179;t2 #负数看左尾,正数看右尾t1,t2的值可以对应上图1,不同模型对应输入,是一个2倍法则
代码运行结果:

观察p-value的值,两值均大于0.05,接受原假设,残差序列为白噪声序列,且t1,t2均大于1.984723,(2倍法则)说明拟合模型有效。
10 预测未来趋势
forecast为预测函数
h=_为预测的年数,h=5就是预测未来五年
xfore<-forecast(x.fit,h=5);xfore#forecast预测plot(xfore, col=2)#出现的图形,蓝色的线是预测值,线两侧阴影为85%,95%的置信区间代码运行结果:
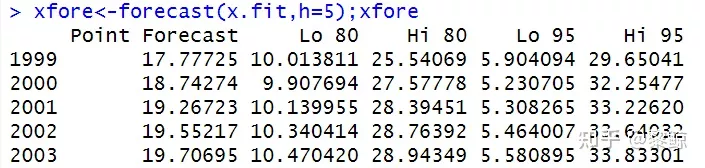
未来五年置信区间
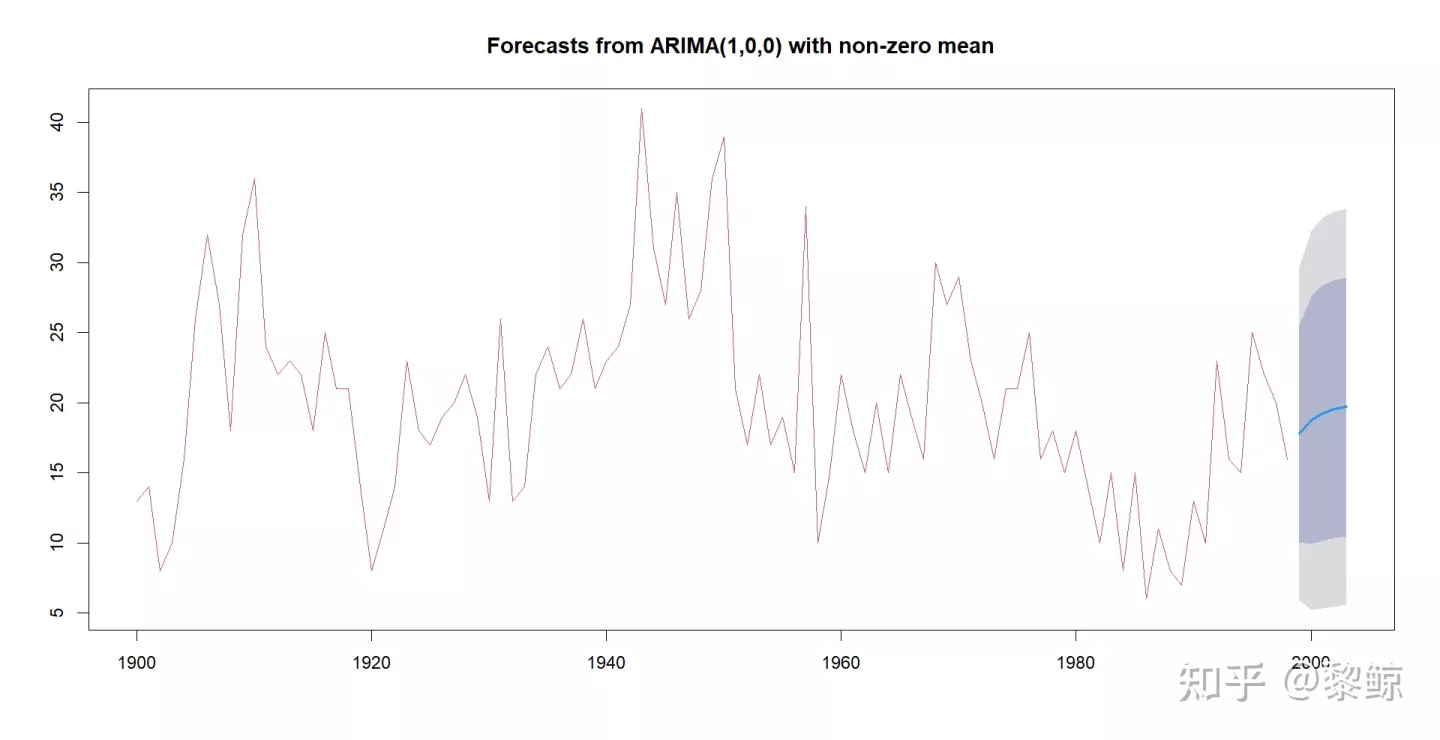
阴影部分为预测区间
结语:
以上关于时间序列图的绘制即检验、预测就完成了。
感谢大家阅读,如果方便的话给个赞同,谢谢!!!