目录
树树的定义树的基本术语二叉树⼆叉树的种类满二叉树完全二叉树 二叉树的性质二叉树的遍历方法前序遍历中序遍历后序遍历层序遍历 二叉树的实现

树
树的定义
树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:①有且仅有一个特定的称为根(Root)的结点;②当n>1时,其余结点可分为m(m>0)个互不相交的有限集 T 1 {T}_{1} T1、 T 2 {T}_{2} T2、… 、 T m {T}_{m} Tm,其中每一个集合本身又是一棵树,并且称为根的子树(Sub Tree)。
树的基本术语
节点的度:一个节点含有的子树的个数称为该节点的度;叶节点或终端节点:度为0的节点称为叶节点;非终端节点或分支节点:度不为0的节点;双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;兄弟节点:具有相同父节点的节点互称为兄弟节点;树的度:一棵树中,最大的节点的度称为树的度;节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;树的高度或深度:树中节点的最大层次;堂兄弟节点:双亲在同一层的节点互为堂兄弟;节点的祖先:从根到该节点所经分支上的所有节点;子孙:以某节点为根的子树中任一节点都称为该节点的子孙。森林:由m(m>=0)棵互不相交的树的集合称为森林;二叉树
二叉树是数据结构中一种重要的数据结构,也是树表家族最为基础的结构。
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
⼆叉树的种类
⼆叉树有两种主要的形式:满⼆叉树和完全⼆叉树。
满二叉树
在一棵二叉树中,如果所有的分支节点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树成为满二叉树。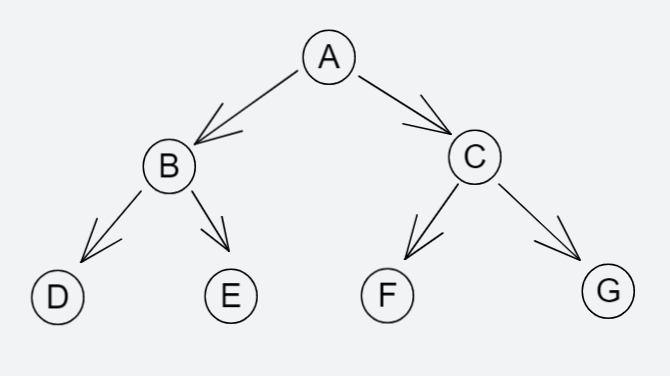
完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为 i(1 ≤ i ≤ n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同,则这棵二叉树称为完全二叉树
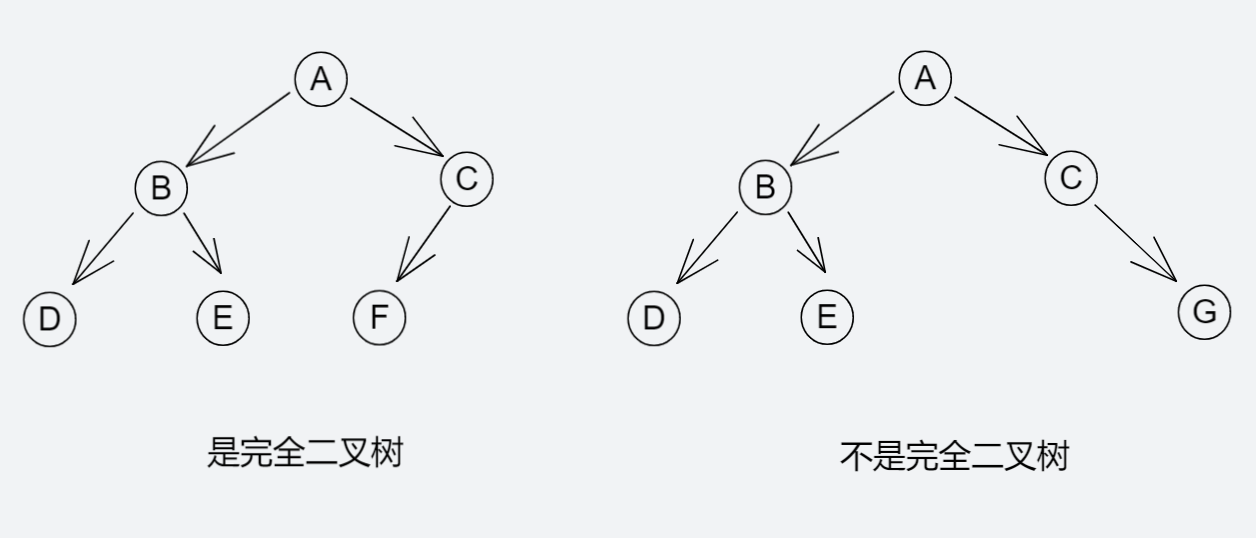
二叉树的性质
二叉树的第 i 层至多有 2 i − 1 {2}^{i-1} 2i−1个结点;深度为 k 的二叉树至多有 2 k {2}^{k} 2k-1个结点;对任何一棵二叉树T TT ,如果其终端结点数为 n 0 {n}_{0} n0,度为2的结点数为 n 2 {n}_{2} n2,则 n 0 {n}_{0} n0= n 2 {n}_{2} n2+1。二叉树的遍历方法
二叉树的遍历方式主要可以分为四种:前序遍历、中序遍历、后序遍历和层序遍历。
前序遍历
简单记为中左右,也就是说先访问根节点,然后前序遍历左子树,再前序遍历右子树。
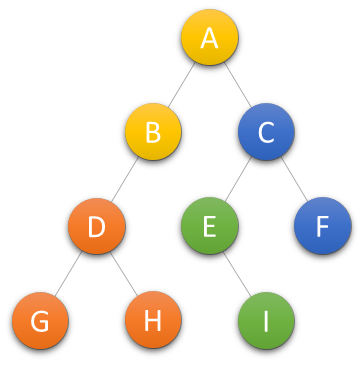
遍历的顺序为ABDGHCEIF
中序遍历
简单记为左中右,也就是说先访问二叉树最左边的结点,然后再访问中间的结点,最后再访问右边的结点。·
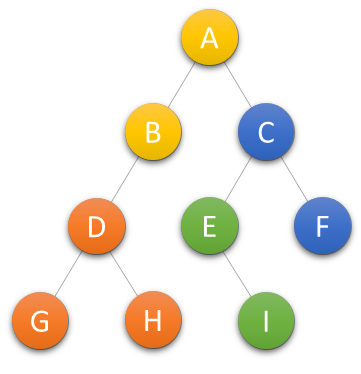
遍历的顺序为GDHBAEICF
后序遍历
简单记为左右中,也就是说先访问二叉树最左边的结点,然后再访问右边的结点,最后再访问中间的结点。·
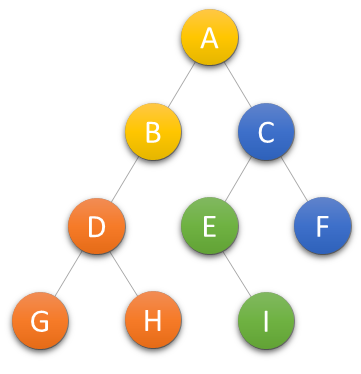
遍历的顺序为GHDBIEFCA
层序遍历
从根结点开始访问,从上而下逐层遍历,在同一层中·,按从左到右的顺序对结点逐个访问。
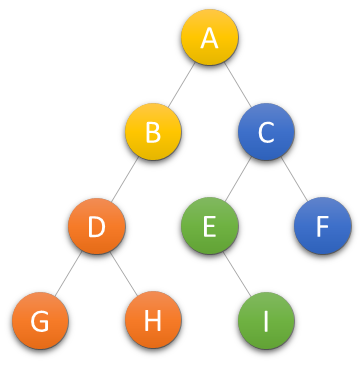
遍历的顺序为ABCDEFGHI
前序遍历、中序遍历和后序遍历就是中的位置不一样,前序遍历就是中左右,中序遍历就是左中右,后序遍历就是左右中。
前中后序遍历都是深度搜索,层序遍历是广度搜索。
二叉树的实现
⼆叉树的定义
struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}};前序遍历
class Solution {public: void traversal(TreeNode* cur, vector<int>& vec) { if (cur == NULL) return; vec.push_back(cur->val); // 中 traversal(cur->left, vec); // 左 traversal(cur->right, vec); // 右 } vector<int> preorderTraversal(TreeNode* root) { vector<int> result; traversal(root, result); return result; }};中序遍历
void traversal(TreeNode* cur, vector<int>& vec) { if (cur == NULL) return; traversal(cur->left, vec); // 左 vec.push_back(cur->val); // 中 traversal(cur->right, vec); // 右}后序遍历
void traversal(TreeNode* cur, vector<int>& vec) { if (cur == NULL) return; traversal(cur->left, vec); // 左 traversal(cur->right, vec); // 右 vec.push_back(cur->val); // 中}?我的个人主页 ?欢迎各位→点赞? + 收藏⭐️ + 留言? ?总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 ? ✉️今天你做别人不想做的事,明天你就能做别人做不到的事♐