前言：
状态压缩DP一般是基于二进制进行的，读者需要对位运算有一定的前置知识
状态压缩DP一般分为两类：
①基于连通性DP（棋盘式）
②集合式（表示每一个元素是否在集合中）
目录
1.状压DP定义:
2. 算法分析：
3.代码
4.优化
5.另一种类型的状态压缩(1条消息) 状态压缩DP 图文详解（二）_Dream.Luffy的博客-CSDN博客
本文讲的是第一类，基于连通性DP
状压DP定义:
动态规划算法的过程是随着阶段的增长，在每个状态维度上的分界点组成了DP拓展的轮廓。对于某些问题，我们需要在动态规划的状态中记录一个集合，保存这个轮廓的详细信息，以便于进行状态转移。若集合大小不超过 N ，集合中每个元素都是小于 k 的自然数，则我们可以把这个集合看做一个 N 位 k 进制数，以一个 [0,k^N-1] 之间的十进制整数的形式作为DP状态的一维。这种把集合转化为整数记录在DP状态中的一类算法被称之为状态压缩动态规划算法。
我们先用一个例子来说明状态压缩DP的一般解法：
例一: 小国王
在n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。
输入格式
共一行，包含两个整数 n 和 k。
输出格式
共一行，表示方案总数，若不能够放置则输出0。
数据范围
1≤n≤10,
0≤k≤n^2
输入样例：
3 2输出样例：
16
国王攻击范围示意图
红色表示国王位置，蓝色表示攻击范围
算法分析：
类似于棋盘放置类问题， 在一般情况下我们会采用暴搜（如八皇后问题）,但如果我们直接暴搜，时间复杂度为O（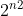
）,明摆着会超时的，因此可以考虑用记忆化搜索来优化。
于是我们用动态规划来考虑这个问题：
动态规划的转移方程，一般由最后一个不同点来定，由国王攻击方式我们可以发现，
第i层放置国王的行为受到第i - 1层和第 i + 1 层以及第 i 层国王影响。
那么我们可以按照一般套路，从上往下枚举每一行，这样考虑第 i 层状态时，只需考虑 i−1 层的状态即可。
于是，我们可以考虑把层数 i 作为动态规划的 一个阶段 进行 线性DP，
根据一般的DP思考方式，我们记录第i阶段所需要的信息
第 i 阶段需要记录的就是前 i 层放置的国王数量 j，以及在第 i 层的 棋盘状态 s
这里，我们先分析一下，哪些棋盘状态是合法的， 以及哪些棋盘转移的状态是合法的（注意这两个状态，后面代码实现时会用到）
合法的棋盘状态：
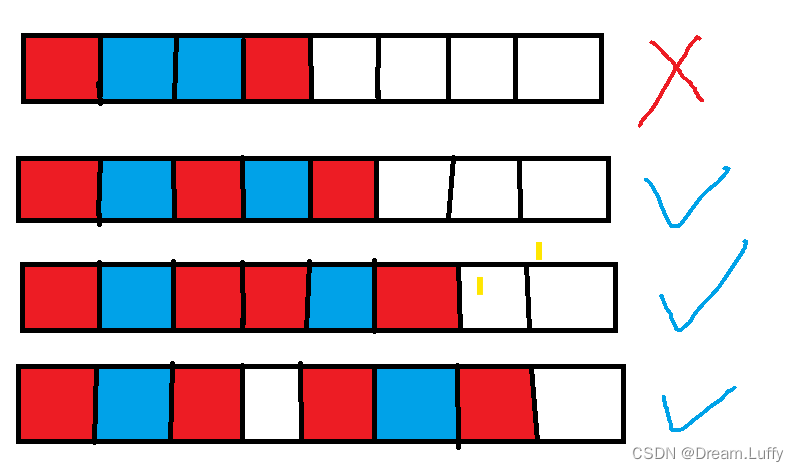
如上图所示，蓝色方块为摆放国王的位置，红色方块为国王的 攻击范围
只要任意王之间只要不相邻，那么就是合法的状态
棋盘转移的合法状态：
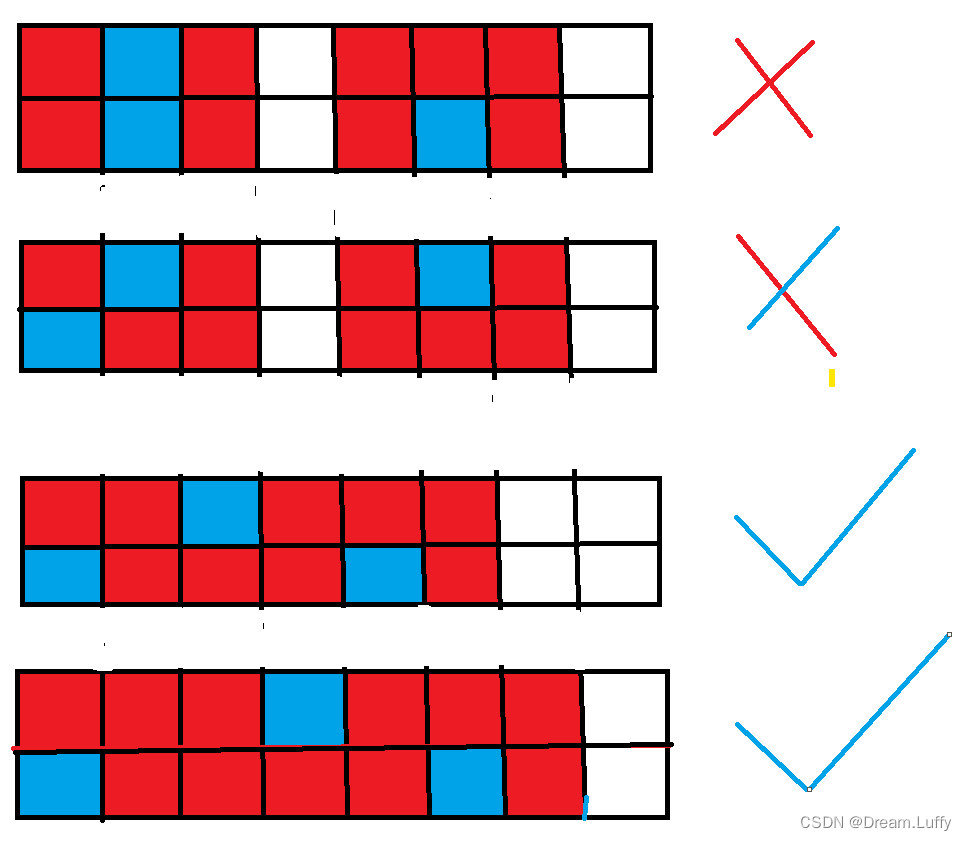
如上图所示：
只要任意国王的 纵坐标不相邻，就是 合法的转移状态。
那么怎么用代码实现表示这些状态呢？
我们可以用二进制来表示这些状态
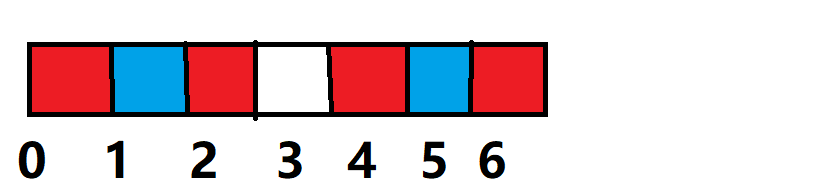
我们给它标上号，让有国王的位置设为1，没国王的位置设为0，于是可以得到(0100010)
于是，我们可以用(state >> i ) == 1, 来判断在当前状态s下的第i个位置(0 <= i < n)是否放了国王。
同时，因为枚举i-1层的状态和第i层的状态所需的循环过多导致时间复杂度很高,所以在这里我们运用预处理的方式来解决此题
状态表示：f[ i ][ j ][ s ]所有只摆了前i行，已经摆了j个国王并且第i行摆放状态是s的所有方案集合
状态转移方程：f[ i ][ j ][ state[a] ] += f[ i - 1 ][ j - c ][ state[b] ] (c是在选择状态a时，放置的国王数量)
状态分析图：(我们把第i行国王的放置方式，作为集合)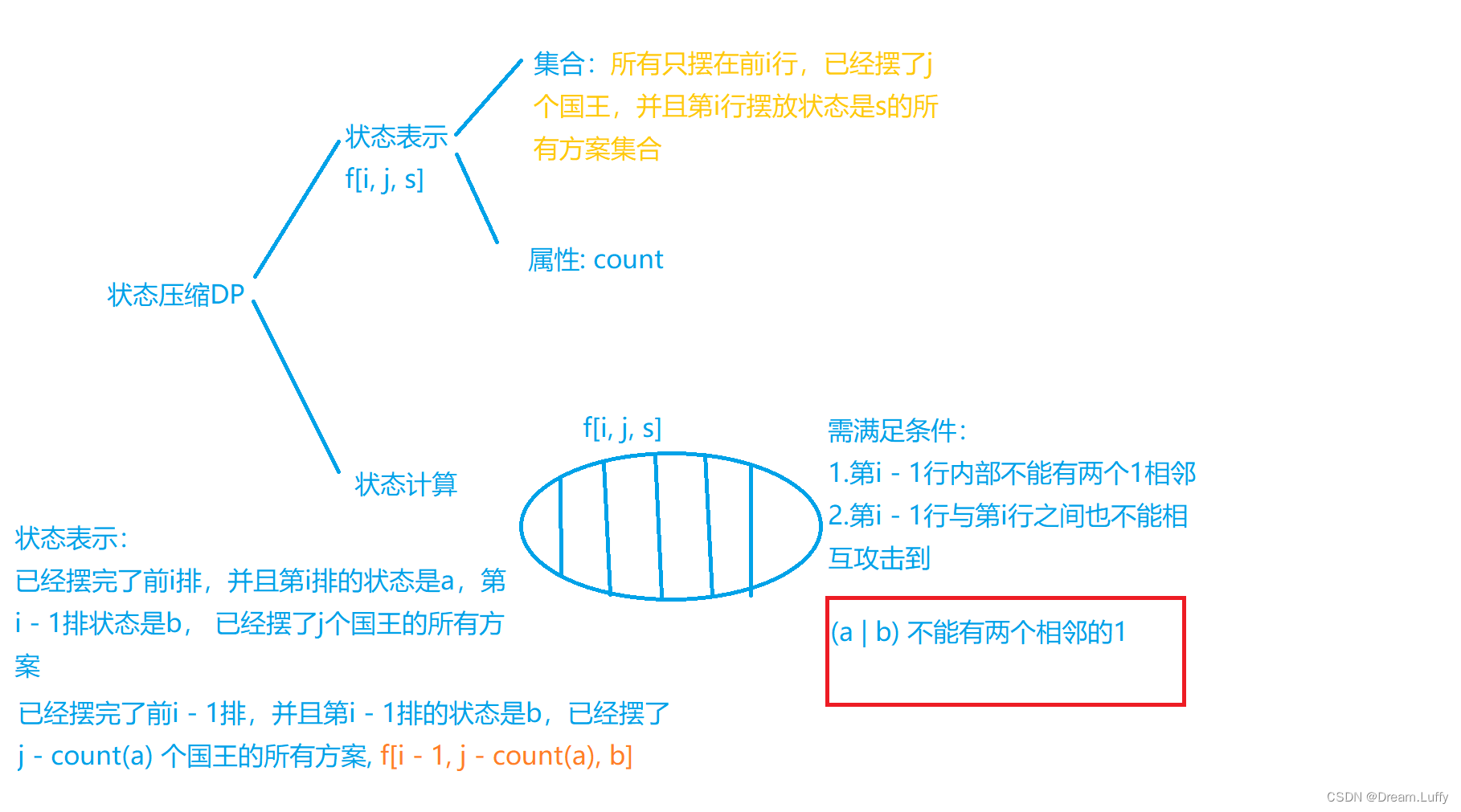
代码
#include<iostream>#include<cstring>#include<algorithm>#include<vector>using namespace std;typedef long long LL;const int N = 12, M = 1 << 10, K = 110;int n, m;vector<int> state;int cnt[M]; //状态state[a]的国王个数vector<int> head[M];//head[i] 里存储在第i行状态为state[a]的情况下，上一行状态可以取到的合法状态statep[b]LL f[N][K][M]; //状态转移方程，存方案数bool check(int state){ for(int i = 0;i < n;i ++) //同一行两个国王不能相邻 if((state >> i & 1) && (state >> i + 1 & 1)) return false; return true;}int count(int state) //统计该状态下国王，即1的个数{ int res = 0; for(int i = 0;i < n;i ++) res += state >> i & 1; return res;}int main(){ cin >>n >> m; //预处理所有合法状态 (对于这两个状态压缩有疑惑的，看看上面的图) for(int i = 0;i < 1 << n;i ++) if(check(i)) { state.push_back(i); //将合法方案存入state cnt[i] = count(i); } //预处理所有合法状态的合法转移 for(int i = 0;i < state.size();i ++) for(int j = 0;j < state.size();j ++) { int a = state[i], b = state[j]; if((a & b) == 0 && check(a | b)) //a & b 指第i行和i-1行不能在同列有国王， check(a|b) == 1 指i和i -1行不能相互攻击到 head[i].push_back(j); //head[i] 里存储在第i行状态为state[a]的情况下，上一行状态可以取到的合法状态statep[b] } f[0][0][0] = 1; //求方案数时，初始方案需要为1,因为全部空 也是一种方案 for(int i = 1;i <= n + 1;i ++) //枚举每一行 for(int j = 0;j <= m;j ++) //国王数量 for(int a = 0;a < state.size();a ++) //枚举合法方案 for(int b : head[a]) { int c = cnt[state[a]]; //状态state[a]的国王个数 if(j >= c) f[i][j][state[a]] += f[i - 1][j - c][state[b]]; //f[i][state[a]], 在第i行状态为i时，所有i - 1行的状态数量 //因为state[a]和a呈映射关系，所也可以写成 // f[i][j][a] += f[i - 1][j - c][b]; } cout << f[n + 1][m][0] << endl;//我们假设摆到n + 1行，并且另这一行状态为0,那么即得到我们想要的答案， //如果我们用f[n][m][]来获取答案，那么我们就要枚举最后一行的所有状态取最大值，来得到答案。java代码:
import java.util.*;public class Main{ static int N = 12,M = 1 << 10,K = 110; static int n,m; //当前走到了第i行,并且已经放了j个国王,且当前第i行的状态是s的方案的集合 static long[][][] f = new long[N][K][M]; static List<Integer> state = new ArrayList<>();//存所有合法状态 static ArrayList<Integer>[] head = new ArrayList[M];//存合法状态所有能够走到的其他状态 static int[] cnt = new int[M];//存每个合法状态对应有多少个1 //判断是不是没有两个相邻的1 public static boolean check(int state){ for (int i = 0 ; i < n ; i ++ ) if ((state >> i & 1) == 1 && (state >> i + 1 & 1 ) == 1) return false; return true; } //统计这个state有多少位是1 public static int count(int state){ int res = 0; for(int i = 0 ; i < n ; i ++ ){ if ((state >> i & 1) == 1){ res ++; } } return res; } public static void main(String[] args){ Scanner scan = new Scanner(System.in); n = scan.nextInt(); m = scan.nextInt(); //首先将所有合法状态找出来 for (int i = 0 ; i < 1 << n ; i ++ ){ if (check(i)){ //如果合法 state.add(i);//将他存下来 cnt[i] = count(i);//然后计算一下这个状态有多少个1 } } //接下来是寻找合法状态所有能够走到的其他状态 for (int i = 0 ; i < state.size(); i ++ ){ for (int j = 0 ; j < state.size(); j ++ ){ int a = state.get(i); int b = state.get(j); if ((a & b) == 0 && check(a | b)){ //如果这个数a还没有存过数，那就新建一个a链表放 if(head[i] == null){ head[i] = new ArrayList<>(); } //创建完之后才能放 head[i].add(j); } } } //初始化 f[0][0][0] = 1; for (int i = 1 ; i <= n + 1; i ++ ){ for (int j = 0 ; j <= m ; j ++ ){ for (int a = 0; a < state.size(); a ++ ){ for (int b : head[a]){ int c = cnt[state.get(a)]; if(j >= c){ f[i][j][a] += f[i - 1][j - c][b]; } } } } } System.out.println(f[n + 1][m][0]); }}优化
通常，在内存限制较紧时，我们可以利用滚动数组来优化
由于第 i 阶段状态只会用到第 i−1 阶段的状态，因此我们可以采用滚动数组来优化空间
也就是在枚举行时，将数组下标&1, 这样得到的值都是0 或 1 ，以此进行空间的优化
//滚动数组优化#include<iostream>#include<cstring>#include<algorithm>#include<vector>using namespace std;typedef long long LL;const int N = 12, M = 1 << 10, K = 110;int n, m;vector<int> state;int cnt[M];vector<int> head[M];LL f[2][K][M];bool check(int state){ for(int i = 0;i < n;i ++) //同一行两个国王不能相邻 if((state >> i & 1) && (state >> i + 1 & 1)) return false; return true;}int count(int state) //统计该状态下国王，即1的个数{ int res = 0; for(int i = 0;i < n;i ++) res += state >> i & 1; return res;}int main(){ cin >>n >> m; for(int i = 0;i < 1 << n;i ++) if(check(i)) { state.push_back(i); //将合法方案存入state cnt[i] = count(i); } for(int i = 0;i < state.size();i ++) for(int j = 0;j < state.size();j ++) { int a = state[i], b = state[j]; if((a & b) == 0 && check(a | b)) //上下排兼容的情况 head[i].push_back(j); } f[0][0][0] = 1; for(int i = 1;i <= n + 1;i ++) //枚举每一行 for(int j = 0;j <= m;j ++) //国王数量 for(int a = 0;a < state.size();a ++) //枚举合法方案 { f[i & 1][j][state[a]] = 0;//要先清空,因为第一维一直在循环,转移用的 += ，不清空会用到前前阶段的状态 for(int b : head[a]) { int c = cnt[state[a]]; if(j >= c) f[i & 1][j][state[a]] += f[i - 1 & 1][j - c][state[b]]; //因为state[a]和a呈映射关系，所也可以写成 // f[i][j][a] += f[i - 1][j - c][b]; } } cout << f[n + 1 & 1][m][0] << endl; return 0; }这里，还有搜索算法哦，手把手 图文分析, 包教包会
BFS之 Flood Fill算法_Dream.Luffy的博客-CSDN博客
另一种类型的状态压缩(1条消息) 状态压缩DP 图文详解（二）_Dream.Luffy的博客-CSDN博客
该系列会持续更新, 我是Luffy，期待与你再次相遇
