文章目录
参考资料1. 简介2. 基本思想3. 算法精讲4. 算法步骤5. python实现
参考资料
路径规划与轨迹跟踪系列算法蚁群算法原理及其实现蚁群算法详解(含例程)图说蚁群算法(ACO)附源码蚁群算法Python实现1. 简介
蚁群算法(Ant Colony Algorithm, ACO) 于1991年首次提出,该算法模拟了自然界中蚂蚁的觅食行为。蚂蚁在寻找食物源时, 会在其经过的路径上释放一种信息素,并能够感知其它蚂蚁释放的信息素。 信息素浓度的大小表征路径的远近, 信息素浓度越高, 表示对应的路径距离越短。通常, 蚂蚁会以较大的概率优先选择信息素浓度较高的路径, 并释放一定量的信息素, 以增强该条路径上的信息素浓度, 这样,会形成一个正反馈。 最终, 蚂蚁能够找到一条从巢穴到食物源的最佳路径, 即距离最短。
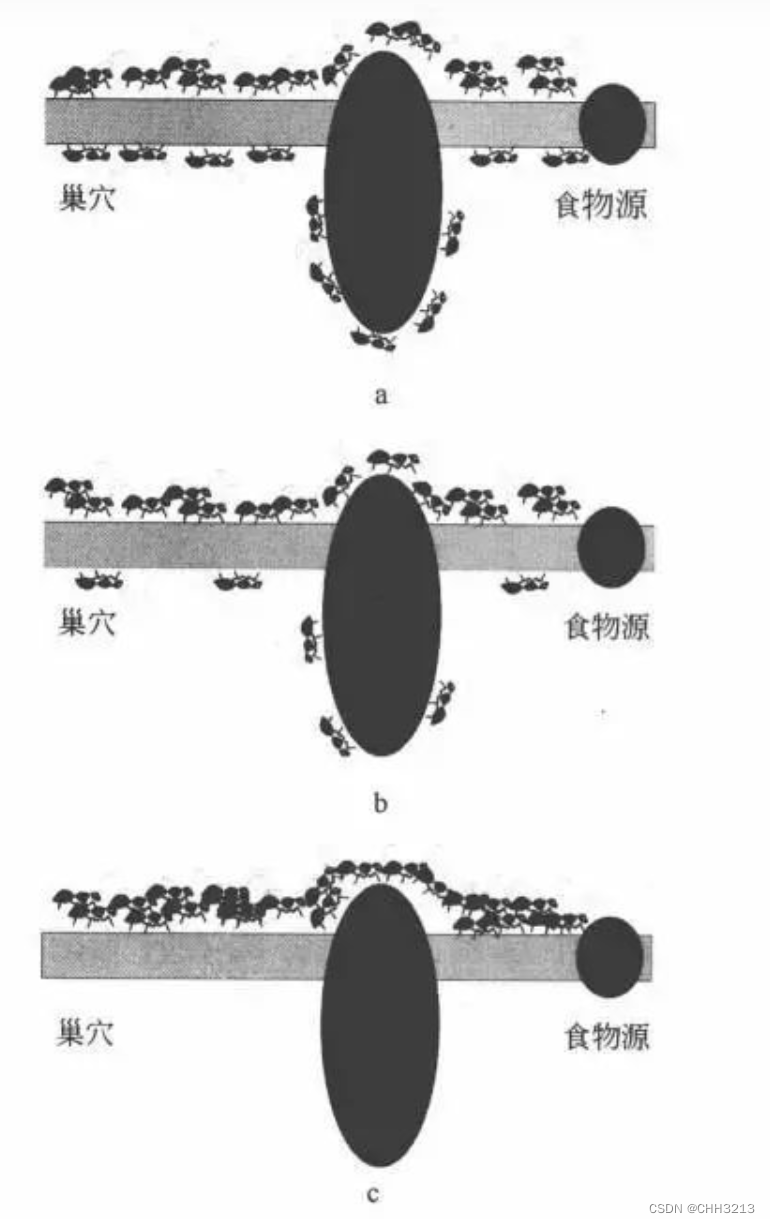
2. 基本思想
用蚂蚁的行走路径表示待优化问题的可行解, 整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多, 随着时间的推进, 较短的路径上累积的信息素浓度逐渐增高, 选择该路径的蚂蚁个数也愈来愈多。最终, 整个蚂蚁会在正反馈的作用下集中到最佳的路径上, 此时对应的便是待优化问题的最优解。3. 算法精讲
不失一般性,我们定义一个具有N个节点的有权图 G = ( N , A ) G=(N,A) G=(N,A),其中N表示节点集合 N = 1 , 2 , . . . , n N={1,2,...,n} N=1,2,...,n,A表示边, A = ( i , j ) ∣ i , j ∈ N A={(i,j)|i,j\in N} A=(i,j)∣i,j∈N。节点之间的距离(权重)设为 ( d i j ) n × n (d_{ij})_{n\times n} (dij)n×n,目标函数即最小化起点到终点的距离之和。
设整个蚂蚊群体中蚂蚊的数量为 m m m, 路径节点的数量为 n n n, 节点 i i i 与节点 j j j 之间的相互距离为 d i j ( i , j = 1 , 2 , … , n ) , t d_{i j}(i, j=1,2, \ldots, n), t dij(i,j=1,2,…,n),t时刻节点 i i i 与节点 j j j 连接路径上的信息素浓度为 τ i j ( t ) \tau_{i j}(t) τij(t) 。初始时刻, 各个节点间连接路径上的信息素浓度相同, 不妨设为 τ i j ( 0 ) = τ 0 \tau_{i j}(0)=\tau_{0} τij(0)=τ0。
蚂蚁 k ( k = 1 , 2 , … , m ) k(k=1,2, \ldots, m) k(k=1,2,…,m) 根据各个节点间连接路径上的信息素浓度决定其下一个访问节点, 设 P i j k ( t ) P_{i j}^{k}(t) Pijk(t) 表示 t t t 时刻蚂蚊 k k k 从节点 i i i 转移到节点 j j j 的概率, 其计算公式如下:
P i j k = { [ τ i j ( t ) ] α ⋅ [ η i j ( t ) ] β ∑ s ∈ allow k [ τ i s ( t ) ] α ⋅ [ η i s ( t ) ] β s ∈ allow k 0 s ∉ allow k (1) \tag{1} P_{i j}^{k}= \begin{cases}\frac{\left[\tau_{i j}(t)\right]^{\alpha} \cdot\left[\eta_{i j}(t)\right]^{\beta}}{\sum_{s \in \text { allow }_{k}}\left[\tau_{i s}(t)\right]^{\alpha} \cdot\left[\eta_{i s}(t)\right]^{\beta}} & s \in \text { allow }_{k} \\ 0 & s \notin \text { allow }_{k}\end{cases} Pijk=⎩⎨⎧∑s∈ allow k[τis(t)]α⋅[ηis(t)]β[τij(t)]α⋅[ηij(t)]β0s∈ allow ks∈/ allow k(1)
其中,
η i j ( t ) \eta_{i j}(t) ηij(t) 为启发函数, η i j ( t ) = 1 / d i j \eta_{i j}(t)=1 / d_{i j} ηij(t)=1/dij, 表示蚂蚊从节点 i i i 转移到节点 j j j 的期望程度, a l l o w k ( k = 1 , 2 , … , m ) allow_{k}(k=1,2, \ldots, m) allowk(k=1,2,…,m) 为蚂蚁 k k k待访问节点的集合。开始时, a l l o w k allow_{k} allowk中有(n-1)个元素,即包括除了蚂蚁 k k k出发节点的其它所有节点。随着时间的推进, allow k _{k} k 中的元素不断减少, 直至为空, 即表示所有的节点均访问完毕。 α \alpha α 为信息素重要程度因子, 其值越大, 蚂蚁选择之前走过的路径可能性就越大,搜索路径的随机性减弱, 其值越小,蚁群搜索范围就会减少,容易陷入局部最优。一般取值范围为 [ 0 , 5 ] [0,5] [0,5]。 β \beta β 为启发函数重要程度因子, 其值越大, 表示启发函数在转移中的作用越大, 即蚂蚊会以较大的摡率转移到距离短的节点,蚁群就越容易选择局部较短路径,这时算法的收敛速度是加快了,但是随机性却不高,容易得到局部的相对最优。一般取值范围为 [ 0 , 5 ] [0,5] [0,5]。计算完节点间的转移概率后,采用与遗传算法中一样的轮盘赌方法选择下一个待访问的节点。
依据轮盘赌法来选择下一个待访问的节点, 而不是直接按概率大小选择,是因为这样可以扩大搜索范围,进而寻找全局最优,避免陷入局部最优。
首先计算每个个体的累积概率 q j q_{j} qj ,如下式:
q j = ∑ j = 1 l P i j k (2) \tag{2} q_{j}=\sum_{j=1}^{l} P_{i j}^{k} qj=j=1∑lPijk(2)
q j q_{j} qj 相当于转盘上的跨度,跨度越大的区域越容易选到, l l l代表下一步可选路径的数量。
之后随机生成一个 ( 0 , 1 ) (0 , 1) (0,1) 的小数 r \mathrm{r} r,比较所有 q j q_{j} qj 与 r \mathrm{r} r 的大小,选出大于 r r r 的最小的那个 q j , q_{j} , qj, 该 q j q_{j} qj 对应的索引 j j j即为第 k \mathrm{k} k 只蚂蚁在第 i i i条路径时下一步要选择的目标点。
r = rand ( 0 , 1 ) j = index { min [ q j > r ] } (3) \tag{3} \begin{gathered} r=\operatorname{rand}(0,1) \\ j=\operatorname{index}\left\{\min \left[q_{j}>r\right]\right\} \end{gathered} r=rand(0,1)j=index{min[qj>r]}(3)
在蚂蚁释放信息素的同时,各个节点间连接路径上的信息素逐渐消失,设参数 ρ ( 0 < ρ < 1 , 一 般 取 值 为 0.1 \rho(0<\rho<1,一般取值为0.1 ρ(0<ρ<1,一般取值为0.1~ 0.99 ) 0.99) 0.99)表示 信息素的挥发程度。当所有的蚂蚁完成一次循环后,各个节点间链接路径上的信息素浓度需进行更新,计算公式为
{ τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + Δ τ i j Δ τ i j = ∑ k = 1 n Δ τ i j k (4) \tag{4} \left\{\begin{array}{l} \tau_{i j}(t+1)=(1-\rho) \tau_{i j}(t)+\Delta \tau_{i j} \\ \Delta \tau_{i j}=\sum_{k=1}^{n} \Delta \tau_{i j}^{k} \end{array}\right. {τij(t+1)=(1−ρ)τij(t)+ΔτijΔτij=∑k=1nΔτijk(4)
其中, Δ τ i j k \Delta \tau_{i j}^{k} Δτijk表示第 k k k只蚂蚁在节点 i i i与节点 j j j连接路径上释放的信息素浓度; Δ τ i j \Delta \tau_{i j} Δτij表示所有蚂蚁在节点 i i i与节点 j j j连接路径上释放的信息素浓度之和。
蚂蚁信息素更新的模型包括蚁周模型(Ant-Cycle模型)、蚁量模型(Ant-Quantity模型)、蚁密模型(Ant-Density模型)等。
区别:
蚁周模型利用的是全局信息,即蚂蚁完成一个循环后更新所有路径上的信息素;
蚁量和蚁密模型利用的是局部信息,即蚂蚁完成一步后更新路径上的信息素。
| 信息素增量不同 | 信息素更新时刻不同 | 信息素更新形式不同 | |
|---|---|---|---|
| 蚁周模型 | 信息素增量为 Q / L k Q/L_k Q/Lk,它只与搜索路线有关与具体的路径(i,j)无关 | 在第k只蚂蚁完成一次路径搜索后,对线路上所有路径进行信息素的更新 | 信息素增量与本次搜索的整体线路有关,因此属于全局信息更新 |
| 蚁量模型 | 信息素增量为 Q / d i j Q/d_{ij} Q/dij,与路径(i,j)的长度有关 | 在蚁群前进过程中进行,蚂蚁每完成一步移动后更新该路径上的信息素 | 利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新 |
| 蚁密模型 | 信息素增量为固定值Q | 在蚁群前进过程中进行,蚂蚁每完成一步移动后更新该路径上的信息素 | 利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新 |
蚁周模型的 Δ τ i j k \Delta \tau_{i j}^{k} Δτijk计算公式如下
Δ τ i j k = { Q / L k , 第 k 只蚂蚁从城市 i 访问城市 j 0 , 其他 (5) \tag{5} \Delta \tau_{i j}^{k}= \begin{cases}Q / L_{k}, & \text { 第 } \mathrm{k} \text { 只蚂蚁从城市 } \mathrm{i} \text { 访问城市 } \mathrm{j} \\ 0, & \text { 其他 }\end{cases} Δτijk={Q/Lk,0, 第 k 只蚂蚁从城市 i 访问城市 j 其他 (5)
式中 Q Q Q为信息素常数(一个正的常数),表示蚂蚁循环一次所释放的信息素总量。 L k L_{k} Lk为第k只蚂蚁经过路径的总长度。
4. 算法步骤
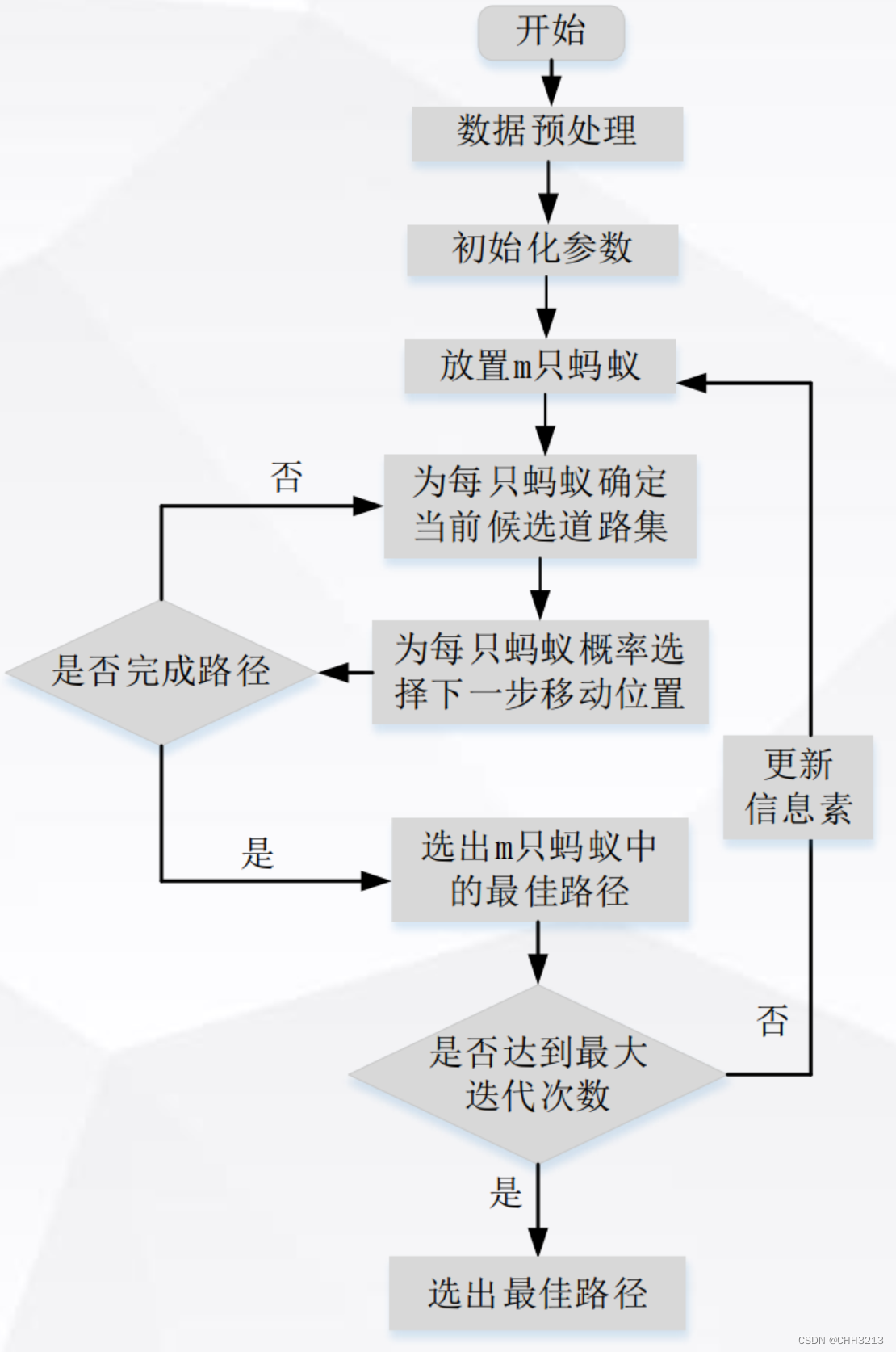
对相关参数进行初始化,如蚁群规模(蚂蚁数量) m m m、信息素重要程度因子 α \alpha α、启发函数重要程度因子 β \beta β、信息素挥发因子 ρ \rho ρ、信息素常数 Q Q Q、最大迭代次数 i t e r m a x itermax itermax。
构建解空间,将各个蚂蚁随机地置于不同的出发点,为每只蚂蚁确定当前候选道路集
更新信息素计算每个蚂蚁经过路径长度 L k ( k = 1 , 2 , … , m ) L_k(k=1,2,…,m) Lk(k=1,2,…,m),记录当前迭代次数中的最优解(最短路径)。同时,对各个节点连接路径上信息素浓度进行更新。
判断是否终止若 i t e r < i t e r m a x iter<itermax iter<itermax,则令 i t e r = i t e r + 1 iter=iter+1 iter=iter+1,清空蚂蚁经过路径的记录表,并返回步骤2;否则,终止计算,输出最优解。
5. python实现
使用蚁群算法解决旅行商问题(TSP),代码来自博客。
import numpy as npimport matplotlib.pyplot as plt# 城市坐标(52个城市)coordinates = np.array([[565.0,575.0],[25.0,185.0],[345.0,750.0],[945.0,685.0],[845.0,655.0], [880.0,660.0],[25.0,230.0],[525.0,1000.0],[580.0,1175.0],[650.0,1130.0], [1605.0,620.0],[1220.0,580.0],[1465.0,200.0],[1530.0, 5.0],[845.0,680.0], [725.0,370.0],[145.0,665.0],[415.0,635.0],[510.0,875.0],[560.0,365.0], [300.0,465.0],[520.0,585.0],[480.0,415.0],[835.0,625.0],[975.0,580.0], [1215.0,245.0],[1320.0,315.0],[1250.0,400.0],[660.0,180.0],[410.0,250.0], [420.0,555.0],[575.0,665.0],[1150.0,1160.0],[700.0,580.0],[685.0,595.0], [685.0,610.0],[770.0,610.0],[795.0,645.0],[720.0,635.0],[760.0,650.0], [475.0,960.0],[95.0,260.0],[875.0,920.0],[700.0,500.0],[555.0,815.0], [830.0,485.0],[1170.0, 65.0],[830.0,610.0],[605.0,625.0],[595.0,360.0], [1340.0,725.0],[1740.0,245.0]])def getdistmat(coordinates): num = coordinates.shape[0] distmat = np.zeros((52, 52)) for i in range(num): for j in range(i, num): distmat[i][j] = distmat[j][i] = np.linalg.norm( coordinates[i] - coordinates[j]) return distmat# #//初始化distmat = getdistmat(coordinates)numant = 45 ##// 蚂蚁个数numcity = coordinates.shape[0] ##// 城市个数alpha = 1 ##// 信息素重要程度因子beta = 5 ##// 启发函数重要程度因子rho = 0.1 ##// 信息素的挥发速度Q = 1 ##//信息素释放总量iter = 0##//循环次数itermax = 200#//循环最大值etatable = 1.0 / (distmat + np.diag([1e10] * numcity)) #// 启发函数矩阵,表示蚂蚁从城市i转移到矩阵j的期望程度pheromonetable = np.ones((numcity, numcity)) #// 信息素矩阵pathtable = np.zeros((numant, numcity)).astype(int) #// 路径记录表distmat = getdistmat(coordinates) #// 城市的距离矩阵lengthaver = np.zeros(itermax) #// 各代路径的平均长度lengthbest = np.zeros(itermax) #// 各代及其之前遇到的最佳路径长度pathbest = np.zeros((itermax, numcity)) #// 各代及其之前遇到的最佳路径长度#//核心点-循环迭代while iter < itermax: #// 随机产生各个蚂蚁的起点城市 if numant <= numcity: #// 城市数比蚂蚁数多 pathtable[:, 0] = np.random.permutation(range(0, numcity))[:numant] else: #// 蚂蚁数比城市数多,需要补足 pathtable[:numcity, 0] = np.random.permutation(range(0, numcity))[:] pathtable[numcity:, 0] = np.random.permutation(range(0, numcity))[ :numant - numcity] length = np.zeros(numant) # 计算各个蚂蚁的路径距离 for i in range(numant): visiting = pathtable[i, 0] # 当前所在的城市 unvisited = set(range(numcity)) # 未访问的城市,以集合的形式存储{} unvisited.remove(visiting) # 删除元素;利用集合的remove方法删除存储的数据内容 for j in range(1, numcity): # 循环numcity-1次,访问剩余的numcity-1个城市 # 每次用轮盘法选择下一个要访问的城市 listunvisited = list(unvisited) probtrans = np.zeros(len(listunvisited)) for k in range(len(listunvisited)): probtrans[k] = np.power(pheromonetable[visiting][listunvisited[k]], alpha) \ * np.power(etatable[visiting][listunvisited[k]], beta) cumsumprobtrans = (probtrans / sum(probtrans)).cumsum() cumsumprobtrans -= np.random.rand() k = listunvisited[(np.where(cumsumprobtrans > 0)[0])[0]] # 元素的提取(也就是下一轮选的城市) pathtable[i, j] = k # 添加到路径表中(也就是蚂蚁走过的路径) unvisited.remove(k) # 然后在为访问城市set中remove()删除掉该城市 length[i] += distmat[visiting][k] visiting = k # 蚂蚁的路径距离包括最后一个城市和第一个城市的距离 length[i] += distmat[visiting][pathtable[i, 0]] # 包含所有蚂蚁的一个迭代结束后,统计本次迭代的若干统计参数 lengthaver[iter] = length.mean() if iter == 0: lengthbest[iter] = length.min() pathbest[iter] = pathtable[length.argmin()].copy() else: if length.min() > lengthbest[iter - 1]: lengthbest[iter] = lengthbest[iter - 1] pathbest[iter] = pathbest[iter - 1].copy() else: lengthbest[iter] = length.min() pathbest[iter] = pathtable[length.argmin()].copy() # 更新信息素 changepheromonetable = np.zeros((numcity, numcity)) for i in range(numant): for j in range(numcity - 1): changepheromonetable[pathtable[i, j]][pathtable[i, j + 1]] += Q / distmat[pathtable[i, j]][ pathtable[i, j + 1]] # 计算信息素增量 changepheromonetable[pathtable[i, j + 1]][pathtable[i, 0]] += Q / distmat[pathtable[i, j + 1]][pathtable[i, 0]] pheromonetable = (1 - rho) * pheromonetable + \ changepheromonetable # 计算信息素公式 if iter%30==0: print("iter(迭代次数):", iter) iter += 1 # 迭代次数指示器+1# 做出平均路径长度和最优路径长度fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(12, 10))axes[0].plot(lengthaver, 'k', marker=u'')axes[0].set_title('Average Length')axes[0].set_xlabel(u'iteration')axes[1].plot(lengthbest, 'k', marker=u'')axes[1].set_title('Best Length')axes[1].set_xlabel(u'iteration')fig.savefig('average_best.png', dpi=500, bbox_inches='tight')plt.show()# 作出找到的最优路径图bestpath = pathbest[-1]plt.plot(coordinates[:, 0], coordinates[:, 1], 'r.', marker=u'$\cdot$')plt.xlim([-100, 2000])plt.ylim([-100, 1500])for i in range(numcity - 1): m = int(bestpath[i]) n = int(bestpath[i + 1]) plt.plot([coordinates[m][0], coordinates[n][0]], [ coordinates[m][1], coordinates[n][1]], 'k')plt.plot([coordinates[int(bestpath[0])][0], coordinates[int(n)][0]], [coordinates[int(bestpath[0])][1], coordinates[int(n)][1]], 'b')ax = plt.gca()ax.set_title("Best Path")ax.set_xlabel('X axis')ax.set_ylabel('Y_axis')plt.savefig('best path.png', dpi=500, bbox_inches='tight')plt.show()