基于DE的小波参数优化在彩色遥感图像降噪中的应用
1. 背景2. 优化模型3.目标函数建模4.实验仿真4.1 实验结果
在先前的工作中,我们使用DE算法优化了小波变换的参数,并用于灰度图像的降噪处理中。但是在现实生活中,彩色图像的降噪应用更加广泛。因此,本文以遥感图像为例,进一步研究了小波参数优化在彩色图像降噪中的应用。
注:先前的研究可看这篇文章:https://blog.csdn.net/qq_43899283/article/details/124014353?spm=1001.2014.3001.5502
1. 背景
遥感图像是由遥感卫星或飞机等载荷设备获取的图像,其受到气象、大气、地表杂波等各种噪声的影响。这些噪声会影响遥感图像的质量,并且会对后续的遥感应用产生不利影响。因此,遥感图像降噪一直是遥感图像处理领域中的一个重要问题。近年来,各种降噪方法在遥感图像处理中得到广泛应用。常用的降噪方法包括小波变换、非局部均值滤波、自适应中值滤波等。其中,小波变换作为一种经典的降噪方法,其基本思想是将图像分解为不同的频带,然后通过去除高频噪声来降低图像噪声。然而,由于噪声分布广泛,搜索适合于解决不同噪声的参数成为一个复杂的优化问题。
2. 优化模型
本文首先将彩色遥感图像划分为三个颜色通道。其次,采用小波变换对所划分出的三通道像素图进行降噪处理。最后,将所三通道降噪图像进行叠加从而得到最终降噪后的图像。其中优化模型如图1所示。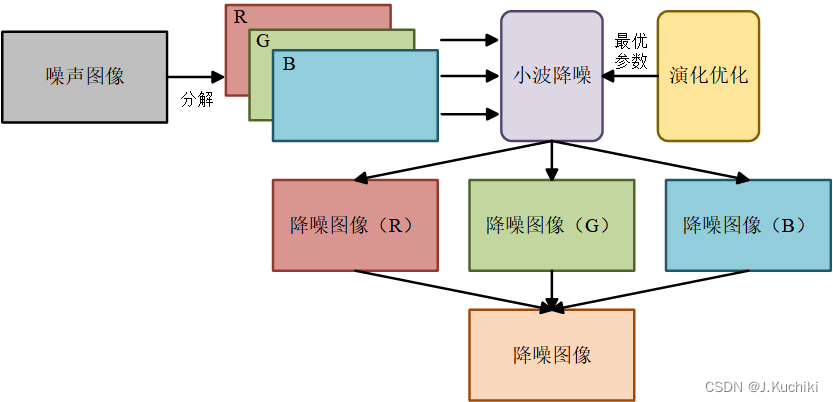 图1:优化模型图
图1:优化模型图
在图1中,小波降噪的最优参数被设定为实数类型的可行解,如下所示:
X = θ N C h , C h ∈ { R , G , B } , N ∈ { 1 , 2 , . . . , 6 } X={θ_N^{Ch}}, Ch∈\{R,G,B\}, N∈\{1,2,...,6\} X=θNCh,Ch∈{R,G,B},N∈{1,2,...,6}其中, C h Ch Ch表示颜色的通道, N N N为每个颜色通道所需的小波降噪优化参数。 X X X的前四个参数代表小波变换所需阈值,第五个参数用来选择合适的小波系,最后一个参数代表小波变换的分解层数。小波变换的分解如图2所示。
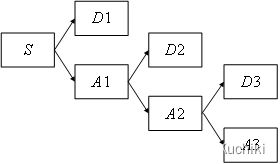
图2:小波变换的分解图
在图2中, S S S是原始信号。 D j ( j ∈ 1 , 2 … n ) Dj (j∈{1,2…n}) Dj(j∈1,2…n)表示高频信号,而 A j ( j ∈ 1 , 2... n ) Aj (j∈{1,2...n}) Aj(j∈1,2...n)表示低频信号。一般来说,分解层越多,噪声的小波系数就越小。
3.目标函数建模
由于PSNR(峰值信噪比)是一种更常用的客观评价方法,因此本文将峰值信噪比(PSNR)作为目标函数来衡量遥感图像降噪的性能。目标函数的表达式如下。
f i t n e s s ( x i M L ) = − P S N R ( x i M L ) fitness(x_i^{ML})=-PSNR(x_i^{ML}) fitness(xiML)=−PSNR(xiML)
将上述适应度函数转换为负数,将问题转换为最小问题,以更好地描述算法的收敛过程。
4.实验仿真
小波系的选用与先前一致,其中选用的遥感图像如下所示。
图3:实验所采用的遥感图像
为其添加密度为0.1的椒盐噪声,效果图如下所示。
图4:生成的噪声图
4.1 实验结果
分别采用DE优化和传统小波系‘sym4’对图4进行降噪处理,结果如下。
图5:采用DE优化后的降噪效果图
图6:采用‘sym4’小波系后的降噪效果图
PSNR值:
| 方法 | PSNR |
|---|---|
| DE | 0.719510747566698 |
| sym4 | 0.632974771660907 |
此处实验仅以‘sym4’小波系为例进行对比,可以发现,采用DE优化后的降噪相比于传统小波降噪具有更好的降噪效果。