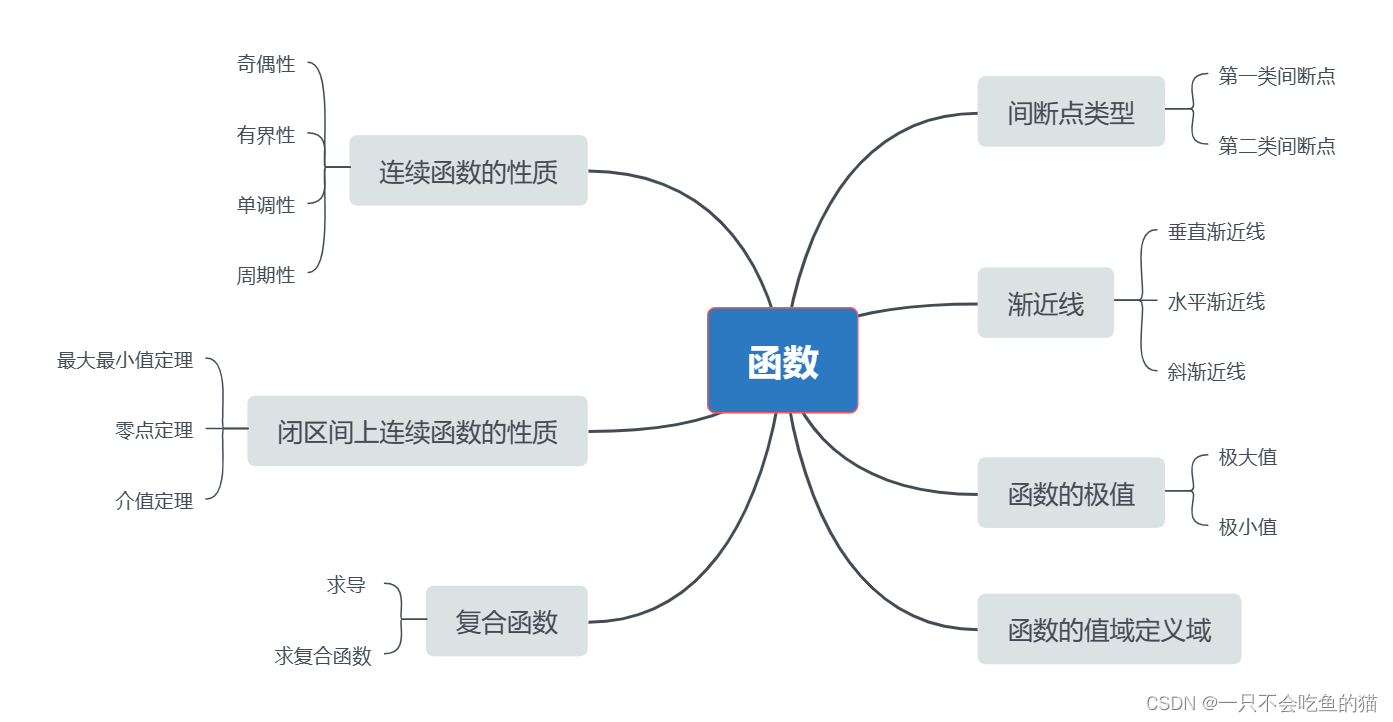
1.连续函数的性质
考点分析
函数的连续性主要考察函数的奇偶性、有界性、单调性、周期性。
例题
===============================================
判断函数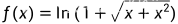 的奇偶性
的奇偶性
===============================================
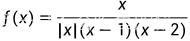 的有界区间为() A.(-1,0) B(0,1) C(1,2) D(2,3)
的有界区间为() A.(-1,0) B(0,1) C(1,2) D(2,3)
===============================================
2.闭区间上连续函数的性质
考点分析
闭区间上连续函数的性质主要考察函数的最大最小值定理、零点定理、介值定理。
3.复合函数
考点分析
复合函数主要考察复合函数的求导以及求出复合函数。
例题
===============================================
设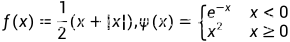 ,求
,求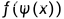
===============================================
4.间断点
考点分析
间断点主要考察间断点的类型,判断间断点所属的类型,间断点一般在分段函数的分段点以及函数的无定义点。
5.渐近线
考点分析
间断点主要考察渐近线的类型,并写出渐近线的方程。
渐近线分为垂直渐近线、斜渐近线、水平渐近线。
一般来说垂直渐近线会在函数的无定义点上,同一趋势下,斜渐近线和水平渐近线不能共存。
6.函数的极值
考点分析
函数的极值主要考察函数的极大值极小值。
通过求一阶导可以得到函数的单调区间,从而判别函数的极值。
一阶导为0的点不一定是极值点
7.函数的值域定义域
考点分析
一般给出函数,求出函数的定义域或是值域。
例题
===============================================
函数 的定义域为()
的定义域为()
===============================================
大纲思维导图
===============================================
===============================================
例题还在逐步完善中
答案在下一篇文章中