密码学的100个基本概念
一、密码学历史二、密码学基础三、分组密码四、序列密码五、哈希函数六、公钥密码七、数字签名八、密码协议九、密钥管理十、量子密码
2022年主要完成了密码学专栏的编写,较为系统的介绍了从传统密码到现代密码,以及量子密码的相关概念。专栏的编写主要参考了 Bruce Schneier 的《应用密码学》以及谷利泽、杨义先的《现代密码学教程》。
密码学作为信息安全的基础,极为重要,本文回顾并总结了密码学中的100个基本概念,供大家学习参考!
一、密码学历史
1.密码学
密码学(cryptography)源于希腊语kryptós“隐藏的”和gráphein“书写”,是研究信息安全保密的学科,涉及密码编码与密码分析。
密码学发展一般分为传统密码学(又分为古典密码、近代密码)和现代密码学两个阶段,以1949年香农(C.E.Shannon)发表的经典论文《保密系统的通信理论》为分界标志。。
2.古典密码
古典密码主要采用代换(Substitution)和置换(Permutation)的方式,并通过手工或简单器械实现,其使用阶段从古代到19世纪末,长达上千年,包括棋盘密码、凯撒密码等。
3.凯撒密码
凯撒密码是罗马皇帝朱利尤斯·凯撒(Julius Caesar)在公元前约50年发明的一种用于战时秘密通信的方法。凯撒密码将字母按字母表的顺序构成一个字母序列链,然后将最后一个字母与第一个字母相连成环,加密方法是将明文中的每个字母用其后的第 k k k个字母代替。
4.近代密码
近代密码一般指20世纪初到20世纪50年代,通过机械或电动设备实现的加密方式,虽然技术上有了很大进步,但加密仍然依靠替代及置换的方式,包括单表代换密码(如仿射密码)、多表代换密码(如Vigenère密码和Hill密码等)。
5.现代密码
1949年香农发表《保密系统的通信理论》(Communication Theory of Secrecy System),标志着现代密码学的开端。香农将信息论引入到密码学研究中,利用概率统计的观点和熵的概念对信息源、密钥源、传输的密文和密码系统的安全性进行了数学描述和定量分析,并提出了对称码体制的模型,为现代密码学奠定了数学基础,这是密码学的第一次飞跃。
1976年,Diffie和Hellman发表的经典论文《密码学的新方向》(New Directions in Cryptography)提出了公钥密码体制思想,为现代密码学的发展开辟了崭新的方向,带来了密码学的第二次飞跃。
二、密码学基础
6.中断
中断(Interruption)也称拒绝服务,是指阻止或禁止通信设施的正常使用或管理,这是对可用性攻击。这种攻击一般有两种形式:一是攻击者删除通过某一连接的所有协议数据单元,从而抑制所有的消息指向某个特殊的目的地;二是使整个网络瘫痪或崩溃,可能采取的手段是滥发消息使之过载,使网络不能正常工作。
7.截取
截取(Interception)是未授权地窃听或监测传输的消息,从而获得对某个资源的访问,这是对机密性的攻击。攻击者一般通过在网络中“搭线”窃听,以获取他们通信的内容。
8.篡改
篡改(Modification)也就是修改数据流,对一个合法消息的某些部分被改变、消息被延迟或改变顺序,以产生一个未授权、有特殊目的的消息,是针对连接的协议数据单元的真实性、完整性和有序性的攻击。
9.伪造
伪造(Fabrication)是指将一个非法实体假装成一个合法的实体,是对身份真实性的攻击,通常与其他主动攻击形式结合在一起才具有攻击效果,如攻击者重放以前合法连接初始化序列的记录,从而获得自己本身没有的某些特权。
10.重放
重放(Replay)将一个数据单元截获后进行重传,产生一个未授权的消息。在这种攻击中,攻击者记录下某次通信会话,然后在以后某个时刻重放整个会话或其中的一部分。
11.机密性
机密性(Confidentiality)是指保证信息不泄露给非授权的用户或实体,确保存储的信息和被传输的信息仅能被授权的各方得到,而非授权用户即使得到信息也无法知晓信息内容。通常通过访问控制阻止非授权用户获得机密信息,通过加密阻止非授权用户获知信息内容。
12.完整性
完整性(Integrity)是指信息未经授权不能进行篡改的特征,确保信息的一致性,即信息在生成、传输、存储和使用过程中不应发生人为或非人为的非授权篡改(插人、修改、删除、重排序等)。一般通过访问控制阻止篡改行为,同时通过消息摘要算法来检验。
13.认证性
认证性(Authentication),或称真实性,指确保一个消息的来源或消息本身被正确地标识,同时确保该标识没有被伪造,通过**数字签名、消息认证码(MAC)**等方式实现。认证分为消息认证和实体认证。
消息认证是指能向接收方保证该消息确实来自于它所宣称的源,实体认证是指在连接发起时能确保这两个实体是可信的,即每个实体确实是它们宣称的那个实体,第三方也不能假冒这两个合法方中的任何一方。14.不可否认性
不可否认性(Non-Repudiation)是指能保障用户无法在事后否认曾经对信息进行的生成、签发、接收等行为,是针对通信各方信息真实性、一致性的安全要求。为了防止发送方或接收方抵赖所传输的消息,要求发送方和接收方都不能抵赖所进行的行为。通过数字签名来提供抗否认服务。
当发送一个消息时,接收方能证实该消息确实是由既定的发送方发来的,称为源不可否认性当接收方收到一个消息时,发送方能够证实该消息确实已经送到了指定的接收方,称为宿不可否认性。15.可用性
可用性(Availability)是指保障信息资源随时可提供服务的能力特性,即授权用户根据需要可以防时访问所需信息,保证合法用户对信息资源的使用不被非法拒绝。
16.密码系统
一个密码系统(体制)至少由明文、密文、加密算法和解密算法、密钥五部分组成。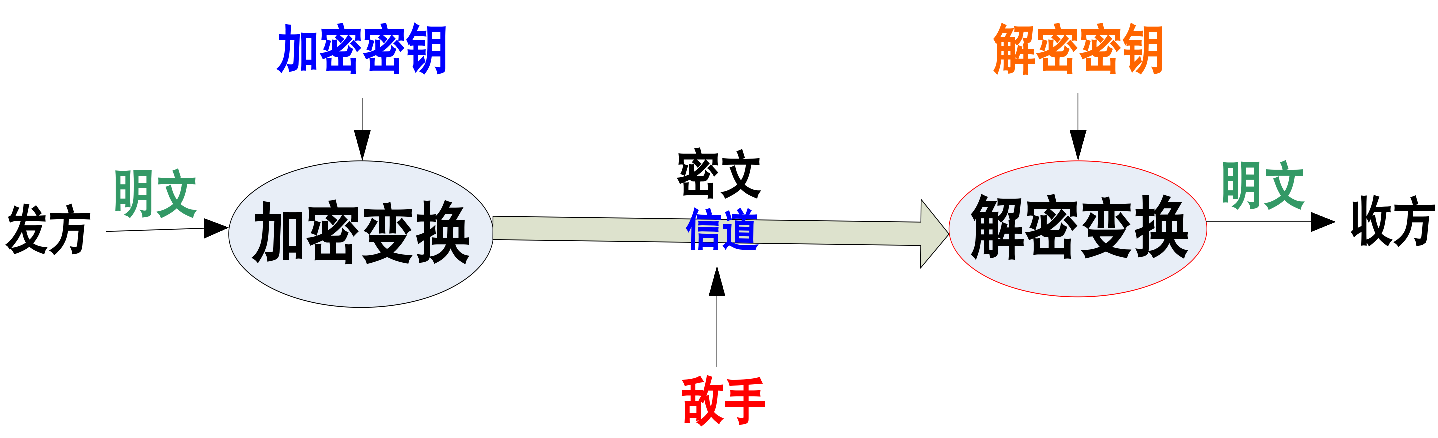
17.明文
信息的原始形式成为明文(Plaintext)。
18.密文
经过变换加密的明文称为密文(Ciphertext)。
19.加密
对明文进行编码生成密文的过程称为加密(Encryption), 编码的规则称为加密算法。
20.解密
将密文恢复出明文的过程称为解密(Decryption),解密的规则称为解密算法。
21.密钥
密钥(Key)是唯一能控制明文与密文之间变换的关键,分为加密密钥和解密密钥。
22.柯克霍夫假设
柯克霍夫假设(Kerckhoffs Assumption),又称柯克霍夫原则(KerckhoffsPrinciple)或柯克霍夫公理(Kerckhoffs Axiom)是荷兰密码学家奥古斯特·柯克霍夫(Auguste Kerckhoffs)于1883年在其名著《军事密码学》中阐明的关于密码分析的一个基本假设:密码系统的安全性不应取决于不易改变的算法,而应取决于可随时改变的密钥,这就是设计和使用密码系统时必须遵守的。即加密和解密算法的安全性取决于密钥的安全性,而加密/解密的算法是公开的,只要密钥是安全的,则攻击者就无法推导出明文。
23.唯密文攻击
唯密文攻击(Ciphertext Only Attack)指密码分析者除了拥有截获的密文外(密码算法公开),无其他可以利用的信息。密码分析者的任务是恢复尽可能多的明文,或者最好是能推算出加密消息的密钥的信息。一般采用穷举搜索法文的尝试,直到得到有意义的明文。理论上穷举搜索是可以成功的,但实际上任何一种能保障安全要求的复杂度都是实际攻击者无法承受的。在这种情况下进行密码破译是最困难的,经不起这种攻击的密码体制被认为是完全不安全的。
24.已知明文攻击
已知明文攻击(Known Plaintext Attack)指密码分析者不仅掌握了相当数量的密文,还有一些已知的明-密文对可供利用。密码分析者的任务是用加密信息推出密钥或导出一个算法,该算法可对用同一密钥加密的任何新的信息进行解密。现代密码体制要求不仅要经受得住唯密文攻击而且要经受得住已知明文攻击。
25.选择明文攻击
选择明文攻击(Chosen Plaintext Attack)指密码分析者不仅能够获得一定数量的明密文对,还可选择任何明文并在使用同一未知密钥的情况下能得到相应的密文。如果攻击者在加密系统中能选择特定的明文消息,则通过该明文消息对应的密文有可能确定密钥的结构或获取更多关于密钥的信息选择明文攻击比已知明文攻击更有效,这种情况往往是密码分析者通过某种手段暂时控制加密机。此类攻击主要用于公开密钥算法,也就是说公开密钥算法必须经受住这攻击。
26.选择密文攻击
选择密文攻击(Chosen Ciphertext Attack)指密码分析者能选择不同的被加密的密文,并还可得到对应的明文密码分析者的售为是推出密钥及其他密文对应的明文。如果攻击者能从密文中选择特定的密文消息,则通过该密文消息对应的明文有可能推导出密钥的结构或产生更多关于密钥的信息。这种情况往往是密码分析者通过某种手段暂时控制解密机。
27.选择文本攻击
选择文本攻击(Chosen Text Attack)是选择明文攻击和选择密文攻击的组合,即密码分析者在掌握密码算法的前提下不仅能够选择明文并得到对应的密文,而且还能选择密文得到对应的明文。这种情况往往是密码分析者通过某种手段暂时控制加密机和解密机。
28.无条件安全
若在一种密码体制中,密码破译者无论知道多少密文以及采用何种方法都得不到明文或是密钥的信息,称其为无条件安全。无条件安全与攻击者的计算能力及时间无关。
29.有条件安全
有条件安全性是根据破解密码系统所需的计算量来评价其安全性,分为计算安全性、实际安全性和可证明安全性。
30.计算安全性
若破解一个密码系统是可行的,但使用已知的算法和现有计算工具不可能完成所要求的计算量,即已有最好的方法破解该密码系统所需要的努力超出了破解者的时间空间和资金等的破解能力,称该密码体制在计算上安全。
31.实际安全性
实际安全是指密码系统满足以下两个准则之一:破解该密码系统的成本超过被加密信息本身的价值;破译该密码系统的时间超过被加密信息的有效生命周期。
32.可证明安全性
可证明安全性是将密码体制的安全性归结为求解某个经过深入研究但尚未解决的数学难题,即将某种密码体制的安全性问题等价为一个数学难题的求解问题。这种判断方法存在的问题是:它只说明了该密码体制的安全和某个数学问题相关,但没有完全证明间题本身的安全性。
33.对称密码体制
对称密码体制(Symmetric Key Cryptosystem)又称单钥密码体制(One Key Cryptosystem)或秘密密钥密码体制(Secret Key Cryptosystem)。对称密码体制中,密钥必须完全保密,且加密密钥和解密密钥相同,或其中的一个可以很容易地推出另一个。典型算法有DES、3DES、AES、IDEA、RC4、A5、SEAL等。
对称密码体制的密钥相对较短,密文的长度往往与明文长度相同,具有较快的加解密速度,易于硬件实现。但发送方如何安全、高效地把密钥送到接收方是对称密码体制的软肋,往往需要“安全通道”;此外称密码体制密钥量大,难于管理。
34.非对称密码体制
1976年,Whitefield Diffie和MartinHellman《密码学的新方向》(New Directions in Cryptography)中开创性的提出了公钥密码体制,又称非对称密码体制(Asymmetric Key Cryptosystem)又称为双钥密码体制(Double Key Cryptosystem)、公开密钥密码体制(Public Key Cryptosystem)。
该体制中,用户A有一对密钥:加密密钥(公钥) P k P_k Pk和解密密钥(私钥) S k S_k Sk,两者是不同的,且从加密密钥(公钥)无法推出解密密钥(私钥)。若B要给A发送加密信息,需要用A的加密密钥(公钥) P k P_k Pk(可在公开目录中查找)加密消息;A收到密文后,用自己的解密密钥(私钥) S k S_k Sk解密密文。
非对称密码体制主要是为了解决对称密码体制中的密钥分发和管理问题,与对称密码体制相比,非对称密码体制加解密速度较慢,密钥较长,密文长度往往大于明文长度。常见公钥密码体制包括基于大整数因子分解问题的RSA公钥密码体制,基于有限域乘法群上的离散对数问题的ElGamal公钥密码体制,基于椭圆曲线上离散对数问题的椭圆曲线公钥密码体制等。
三、分组密码
35.分组密码
分组密码(block cipher)本质是一个从明文空间 P P P( m m m长的比特串集合)到密文空间 C C C( n n n长的比特串集合)的一一映射(一般 m = n = t m=n=t m=n=t)。明文消息经编码表示后的二进制序列 p 0 , p 1 , … , p i , … p0,p1,…,pi, … p0,p1,…,pi,…划分成若干固定长度的组(或块) p = ( p 0 , p 1 , … , p m − 1 ) p=(p_0,p_1,…,p_{m-1}) p=(p0,p1,…,pm−1),各组分别在密钥 k = ( k 0 , k 1 , … , k t − 1 ) k=(k_0,k_1,…,k_{t-1}) k=(k0,k1,…,kt−1)的控制下转换成长度为 n n n的密文分组 c = ( c 0 , c 1 , … , c n − 1 ) c=( c_0,c_1,…,c_{n-1}) c=(c0,c1,…,cn−1)。

分组密码主要提供数据保密性,也可用于构造伪随机数生成器、流密码、认证码和哈希函数。分组密码分为对称分组密码和非对称分组密码(公钥密码),在很多场合一般指是对称分组密码。
36.扩散
扩散(diffusion)指算法使每一比特明文的变化尽可能多地影响到输出密文序列的变化,以便隐蔽明文的统计特性;并且每一位密钥的影响也尽可能迅速地扩展到较多的输出密文比特中去。即扩散的目的是希望密文中的任一比特都要尽可能与明文、密钥相关联,或者说,明文和密钥中任何一比特值得改变,都会在某种程度上影响到密文值的变化(又称雪崩效应),以防止将密钥分解成若干个孤立的小部分,然后各个击破。
37.混乱
混乱(confusion)指在加密变换过程中是明文、密钥以及密文之间的关系尽可能地复杂化,以防密码破译者采用统计分析法进行破译攻击。混乱可以用“搅拌”来形象地解释,将一组明文和一组密文输入到算法中,经过充分混合,最后变成密文。同时要求,执行这种“混乱”作业的每一步都必须是可逆的,即明文混乱以后能得到密文,反之,密文经过逆向混乱操作后能恢复出明文。
38.白化
白化(whitening)是将分组密码算法的输入与一部分密钥异或,并将其输出与另一部分密钥异或的技术,用于阻止密码分析者在已知基本密码算法的前提下获得一组明文/秘文对。
39.雪崩效应
雪崩效应(Avalance Criteria)指输入(明文或密钥)即使只有很小的变化,也会导致输出(密文)产生巨大变化。严格雪崩效应(Strict Avalance Criteria)指当一个输入位发生改变时,输出位将有一半发生改变。
40.代换-置换网络
代换-置换网络(Subsituation Permutation Network)简称SP网络,是由多重**S变换(S盒,混乱)和P变换(P盒,扩散)**组合成的变换网络,是乘积密码的一种常见表现形式。SP网络中的S盒是许多密码算法唯一的非线性部件,其密码强度决定了整个密码算法的强度。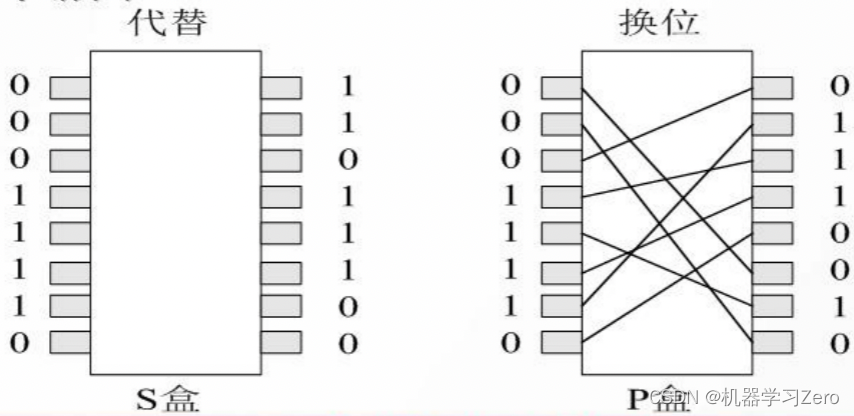
41.Feistel网络
Feistel网络由Feistel提出,将长度为 n n nbit( n n n为偶数)的明文分组分为左右各半长为 n / 2 n/2 n/2的两部分: L L L和 R R R。定义迭代算法如下: L i = R i − 1 L_i = R_{i-1} Li=Ri−1 R i = L i − 1 ⊕ f ( R i − 1 , K i ) R_i = L_{i-1}\oplus f(R_{i-1},K_i) Ri=Li−1⊕f(Ri−1,Ki)其中, K i K_i Ki是第 i i i轮使用的子密钥, f f f是任意轮函数。
Feistel网络保证了算法可逆性,即加密和解密可以采用同一算法实施。
42.DES
DES(Data Encryption Standards)是第一个广泛应用于商用数据保密的密码算法,为对称加密算法。美国国家标准局(NBS,National Bureau of Standards)于1973年开始征集联邦数据加密标准,许多公司提交了算法,IBM公司的Lucifer加密系统最终胜出。经过两年多的公开讨论,1977年1月15日NBS决定利用这个算法,并将其更名为数据加密标准(DES)。
43.AES
1997年美国国家标准与技术研究院(NIST,National Institute of Standards and Technology)公开征集高级加密标准(AES,Advanced Encryption Standard),基本要求是安全性能不低于三重DES,性能比三重DES快,并特别提出高级加密标准必须是分组长度为128位的对称分组密码,且支持长度为128位、192位、256位的密钥。此外,如果算法被选中,在世界范围内须是可免费获得的。
2000年10月2日,NIST宣布最终评选结果,根据安全性(稳定的数学基础、无算法弱点、可抗密码分析)、性能(速度快)、大小(内存与存储空间占用小)、易实现(良好的软硬件适应性)等标准,比利时密码学家Joan Daemen和Vincent Rijmen提出的“Rijndael数据加密算法”最终获胜。修改的Rijndael算法成为高级加密标准AES,2001年11月26日,NIST正式公布高级加密标准AES,并于2002年5月26日正式生效。
44.IDEA
国际数据加密算法(IDEA, International Data Encryption Algorithm)由瑞士的来学嘉(Xuejia Lai)和 James Massey于1990年公布,当时称为推荐加密标准(PES, Proposed Encryption Standard)。1991年,为抗击差分密攻击,他们对算法进行了改进,称为改进推荐加密标准(IPES,Im proved PES),并于1992年改名为国际数据加密算法IDEA。
IDEA受专利保护,要先获得许可证之后才能在商业应用程序中使用,著名的电子邮件隐私技术PGP就是基于IDEA的。
45.分组密码的工作模式
实际消息长度一般大于分组密码的分组长度,分组密码将消息分为固定长度的数据块来逐块处理。人们设计了许多不同的块处理方式,称为分组密码的工作模式,通常是基本密码模块、反馈和一些简单运算的组合。这些工作模式同时为密文分组提供了一些其他性质,如隐藏明文的统计特性、错误传播控制、流密码的密钥流生成等。
46.电子密码本
电子密码本(ECB, Electronic Code Book)模式一次处理一个明文分组,各个明文分组被独立加密成相应的密文分组,主要用于**内容较短且随机的报文(如密钥)**的加密传递。
相同明文(在相同密钥下)得出相同的密文,易受实现统计分析攻击、分组重放攻击和代换攻击链接依赖性:各组的加密都独立于其它分组,可实现并行处理错误传播:单个密文分组中有一个或多个比特错误只会影响该分组的解密结果47.密码分组链接
密码分组链接(CBC, Cipher Block Chaining)模式应用了反馈机制,明文在加密之前需要与前面的密文进行异或,即每个密文分组不仅依赖于产生它的明文分组,还依赖于它前面的所有分组。CBC适合文件加密,是软件加密的最佳选择。
相同的明文,即使相同的密钥下也会得到不同的密文分组,隐藏了明文的统计特性链接依赖性:对于一个正确密文分组的正确解密要求它之前的那个密文分组也正确,不能实现并行处理错误传播:密文分组中的一个单比特错误会影响到本组和其后分组的解密,错误传播为两组48.密码反馈
密码反馈(CFB, Cipher Feedback Block)将消息看作比特流,无需接受完整个数据分组后才能进行加解密,是自同步序列密码算法的典型例子,通常用于加密字符序列。
可用于同步序列密码,具有CBC模式的优点对信道错误较敏感且会造成错误传播数据加解密的速率降低,其数据率不会太高49.输出反馈
输出反馈(OFB, Output Feedback Block)是基于分组密码的同步序列密码算法的一种例子。
CFB模式的一种改进,克服由错误传播带来的问题,但对密文被篡改难于进行检测OFB模式不具有自同步能力,要求系统保持严格的同步,否则难于解密四、序列密码
50.序列密码
序列密码,又称流密码,属于对称密码体制,它一次只对明文消息的单个字符(通常是二进制位)进行加解密变换,具有实现简单、速度快、错误传播少等特点.
在序列密码中,将明文消息按一定长度分组,对各组用相关但不同的密钥逐位加密产生相应密文,相同的明文分组会因在明文序列中的位置不同而对应不同的密文分组,接收者用相同的密钥序列对密文序列逐位解密恢复出明文。
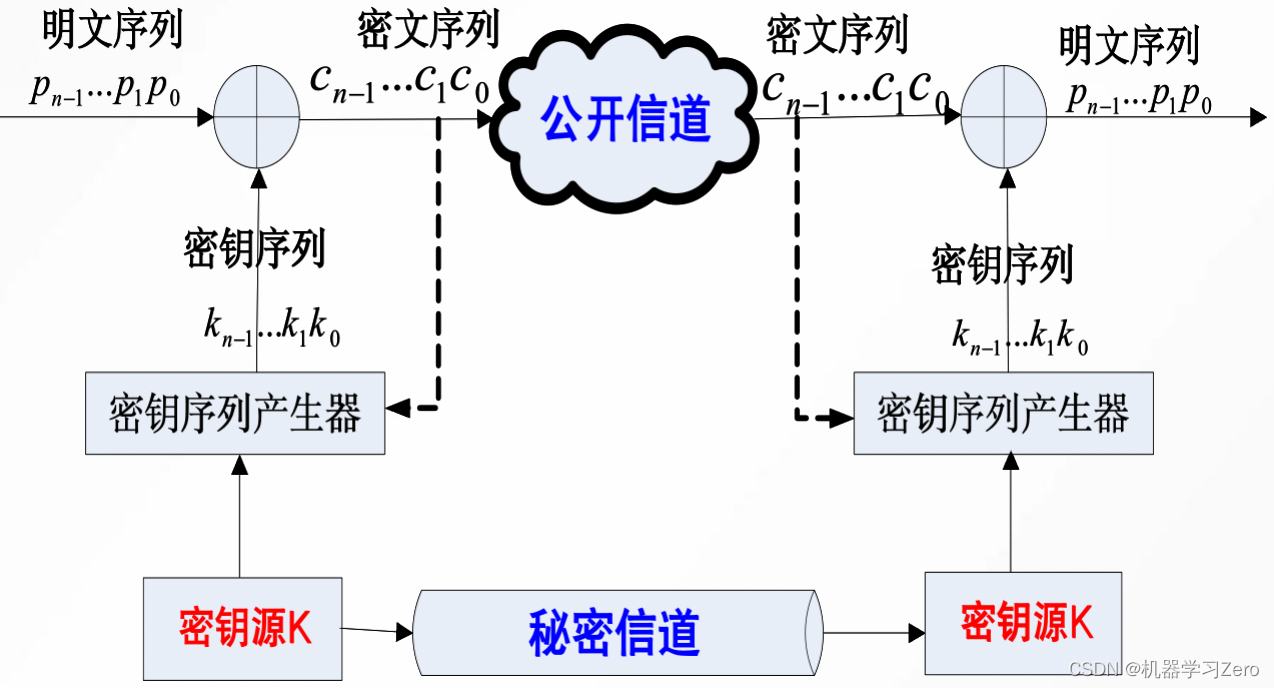
令明文序列 p = p n − 1 . . . p 1 p 0 p=p_{n-1}...p_1p_0 p=pn−1...p1p0密钥序列 k = k n − 1 . . . k 1 k 0 k=k_{n-1}...k_1k_0 k=kn−1...k1k0
密文序列 c = c n − 1 . . . c 1 c 0 = E k n − 1 ( p n − 1 ) . . . E k 1 ( p 1 ) E k 0 ( p 0 ) c=c_{n-1}...c_1c_0=E_{k_{n-1}}(p_{n-1})...E_{k_1}(p_1)E_{k_0}(p_0) c=cn−1...c1c0=Ekn−1(pn−1)...Ek1(p1)Ek0(p0)若 c i = E k i ( p i ) = p i ⊕ k i c_i=E_{k_i}(p_i)=p_i\oplus k_i ci=Eki(pi)=pi⊕ki则称此类为加法序列密码。
51.反馈移位寄存器
反馈移位寄存器(FSR,Feedback Shift Register)一般由移位寄存器和反馈函数(Feedback Function)组成。移位寄存器是由位组成的序列,其长度用位表示,每次移位寄存器中所有位右移一位,最左端的位根据寄存器中某些位计算得到,由寄存器某些位计算最左端位的部分被称为反馈函数,最右端一个寄存器移出的值是输出位。移位寄存器的周期是指输出序列从开始到重复时的长度。
52.线性反馈移位寄存器
线性反馈移位寄存器(LFSR,Linear Feedback Shift Register)的反馈函数是寄存器中某些位简单异或,这些位叫做抽头序列(Tap Sequence),有时也叫 Fibonacci 配置(Fibonacci Configuration)。
53. m m m序列
线性反馈移位寄存器输出序列的性质完全由其反馈函数决定,一个 n n n位LSFR能够处于 2 n − 1 2^{n}-1 2n−1个内部状态中的一个,即理论上, n n n位LFSR在重复之前能够产生 2 n − 1 2^{n}-1 2n−1位长的伪随机序列(由于全0的状态将使LFSR无止尽地输出0序列,因此是 2 n − 1 2^{n}-1 2n−1而不是 2 n 2^{n} 2n)。
只要选择合适的反馈函数便可使序列的周期达到最大值 2 n − 1 2^{n}-1 2n−1,即只有具有一定抽头序列的LFSR才能循环地遍历所有 2 n − 1 2^{n}-1 2n−1个内部状态,这个输出序列被称为** m m m序列**。为了使LFSR成为最大周期LFSR,由抽头序列加上常数1形成的多项式必须是本原多项式,多项式的阶即移位寄存器的长度。
54.RC4
RC4(Ron RivestCipher)以随机置换为基础,是一个可变密钥长度、面向字节操作的序列密码,该算法由于加解密速度快(比DES快约10倍)、易于软件实现,广泛应用于Microsoft Windows、Lotus Notes等软件中,以及安全套接字层(SSL,Secure Sockets Layer)传输信息。
与基于移位寄存器的序列密码不同,RC4是典型的基于非线性数组变换的序列密码。它以一个足够大的数组为基础,对其进行非线性变换,产生非线性的密钥序列,一般把这个大数组称为S盒。RC4的S盒的大小根据参数 n n n(通常 n = 8 n=8 n=8)的值变化,RC4算法理论上可生成总数 N = 2 n N=2^n N=2n个的S盒。
55.A5
A5算法是GSM 系统中要使用的序列密码加密算法之一,用于加密手机终端基站之间的传输的语音和数据,目前已被攻破。
A5算法是一种典型的基于线性反馈移位寄存器的序列密码算法,由一个22bit长的参数(帧号码, Fn)和64 bit长的参数(会话密钥,Kc)生成两个114 bit长的序列(密钥流),然后与GSM会话每帧(228 bit/帧)异或。
五、哈希函数
56.Hash函数
Hash函数也称哈希函数/散列函数、杂凑函数,是一个从消息空间到像空间的不可逆映射,可将“任意”长度的输入经过变换以后得到固定长度的输出。它是一种单向密码体制,即只有加密过程,不存在解密过程。
57.消息摘要
Hash函数的单向性和输出长度固定的特征使其可生成消息的“数字指纹”(Digital Fingerprint),也称消息摘要(MD,Message Digest)或哈希值/散列值(Hash Value),主要应用于消息认证、数字签名、口令的安全传输与存储、文件完整性校验等方面。
58.MD5
MD5算法由美国麻省理工学院著名密码学家Rivest设计,他于1992年向IETF提交的RFC1321中对MD5作了详尽的阐述。MD5是在MD2、MD3、MD4的基础上发展而来,由于在MD4上增加了Safety-Belts,MD5又被称为是“系有安全带的MD4”。
算法的输入是最大长度小于 2 64 2^{64} 264bit的消息,输入消息以 512 512 512+bit的分组为单位处理,输出为 128 b i t 128bit 128bit的消息摘要。
59.SHA1
1993年,美国国家标准技术研究所NIST公布了安全散列算法SHA0(Secure Hash Algorithm)标准,1995年4月17日,公布的修改版本称为SHA-1,是数字签名标准中要求使用的算法。
SHA1算法的输入是最大长度小于 2 64 2^{64} 264bit的消息,输入消息以 512 512 512 bit的分组为单位处理,输出为 160 160 160bit的消息摘要,因此抗穷举性更好。
60.消息认证
消息认证指验证消息的真实性,包括验证消息来源的真实性,一般称之为信息源认证;验证消息的完整性,即验证消息在传输和存储过程中没有被篡改、伪造等
61.消息认证码
消息认证码(MAC,Message Authentication Code)用来检查消息是否被恶意修改,利用消息和双方共享的密钥通过认证函数来生成一个固定长度的短数据块,并将该数据块附加在消息后。
利用DES、AES等对称分组密码体制的密码分组链接模式(CBC)一直是构造MAC的最常见的方法,如FIPS PUB 113中定义的CBC-MAC。由于MD5、SHA-1等Hash函数软件执行速度比DES等对称分组密码算法要快,目前提出了许多基于Hash函数的消息认证算法,其中HMAC(RFC 2014)已作为FIPS 198标准发布,并且在SSL中用于消息认证。
六、公钥密码
62.RSA公钥密码
1978年,美国麻省理工学院的Rivest、Shamir、Adleman联合提出了RSA公钥密码体制,是第一个安全实用的公钥码算法,其安全性依赖于大整数因子分解的困难性。RSA公钥密码体制可用于加密,也可用于数字签名,且具有安全、易实现等特点。
(1)公私密钥对生成
选取两个大素数 p 、 q p、q p、q(不可泄露),计算 n = p q n=pq n=pq及 n n n的欧拉函数 φ ( n ) = ( p − 1 ) ( q − 1 ) \varphi(n) = (p-1)(q-1) φ(n)=(p−1)(q−1)
随机选取整数 e ( 1 < e < φ ( n ) ) e(1<e<\varphi(n)) e(1<e<φ(n))作为公钥,满足 g c d ( e , φ ( n ) ) = 1 gcd(e,\varphi(n))=1 gcd(e,φ(n))=1,即 e e e与 φ ( n ) \varphi(n) φ(n)互素
使用Euclid扩展算法计算私钥 d ≡ e − 1 m o d φ ( n ) d \equiv e^{-1} \bmod \varphi(n) d≡e−1modφ(n),即 e e e的逆元
(2)加解密算法
公钥: ( e , n ) (e,n) (e,n)
私钥: d d d
加密: c ≡ m e m o d n c \equiv m^e \bmod n c≡memodn
解密: m ≡ c d m o d n m \equiv c^d \bmod n m≡cdmodn
63.ElGamal公钥密码
ElGamal公钥密码体制由T.ElGamal于1985年提出,该体制基于有限域上离散对数问题,既可用于加密,又可以用于数字签名。由于其较好的安全性,且同一明文在不同的时刻会生成不同的密文,在实际中得到了广泛的应用,尤其在数字签名方面的应用,著名的**数字签名标准(DSS,Digital Signature Standard)**其实就是ElGamal签名方案的一种变形。
(1)公私密钥对生成
随机选择一个大素数 p p p,且要求 p − 1 p-1 p−1有大素数因子, g ∈ Z p ∗ g \in \boldsymbol Z^{*}_p g∈Zp∗是一个本原元( Z p Z_p Zp是一个有 p p p个元素的有限域, Z p ∗ Z^{*}_p Zp∗是 Z p Z_p Zp中的非零元构成的乘法群)
选一个随机数 x ( 1 < x < p − 1 ) x(1<x<p-1) x(1<x<p−1)作为私钥,计算 y ≡ g x m o d p y \equiv g^x \bmod p y≡gxmodp,公钥为 ( y , g , p ) (y,g,p) (y,g,p)
(2)加解密算法
公钥: ( y , g , p ) (y,g,p) (y,g,p)
私钥: x x x
加密: C = ( c , c ′ ) C = (c,c^{'}) C=(c,c′),其中 c ≡ g r m o d p , c ′ ≡ m y r m o d p c \equiv g^{r} \bmod p, c^{'} \equiv m y^{r} \bmod p c≡grmodp,c′≡myrmodp, r ( 1 < r < p − 1 ) r(1<r<p-1) r(1<r<p−1)为随机数,
解密: m ≡ ( c ′ / c x ) m o d p m \equiv (c^{'}/c^{x}) \bmod p m≡(c′/cx)modp
ElGamal公钥密钥体制每次加密运算需要选择一个随机数,密文既依赖于明文,又依赖于选择的随机数,因此对于同一个明文,不同的时刻生成的密文不同。此外,ElGamal加密使得消息扩展了两倍,即密文的长度是对应明文长度的两倍。
七、数字签名
64.数字签名
数字签名(Digital Signature),也称电子签名,是指附加在某一电子文档中的一组特定的符号或代码。它利用密码技术对该电子文档进行关信息提取并进行认证形成,用于标识签发者的身份以及签发者对电子文档的认可,并能被接收者用来验证该电子文档在传输过程中是否被篡改或伪造。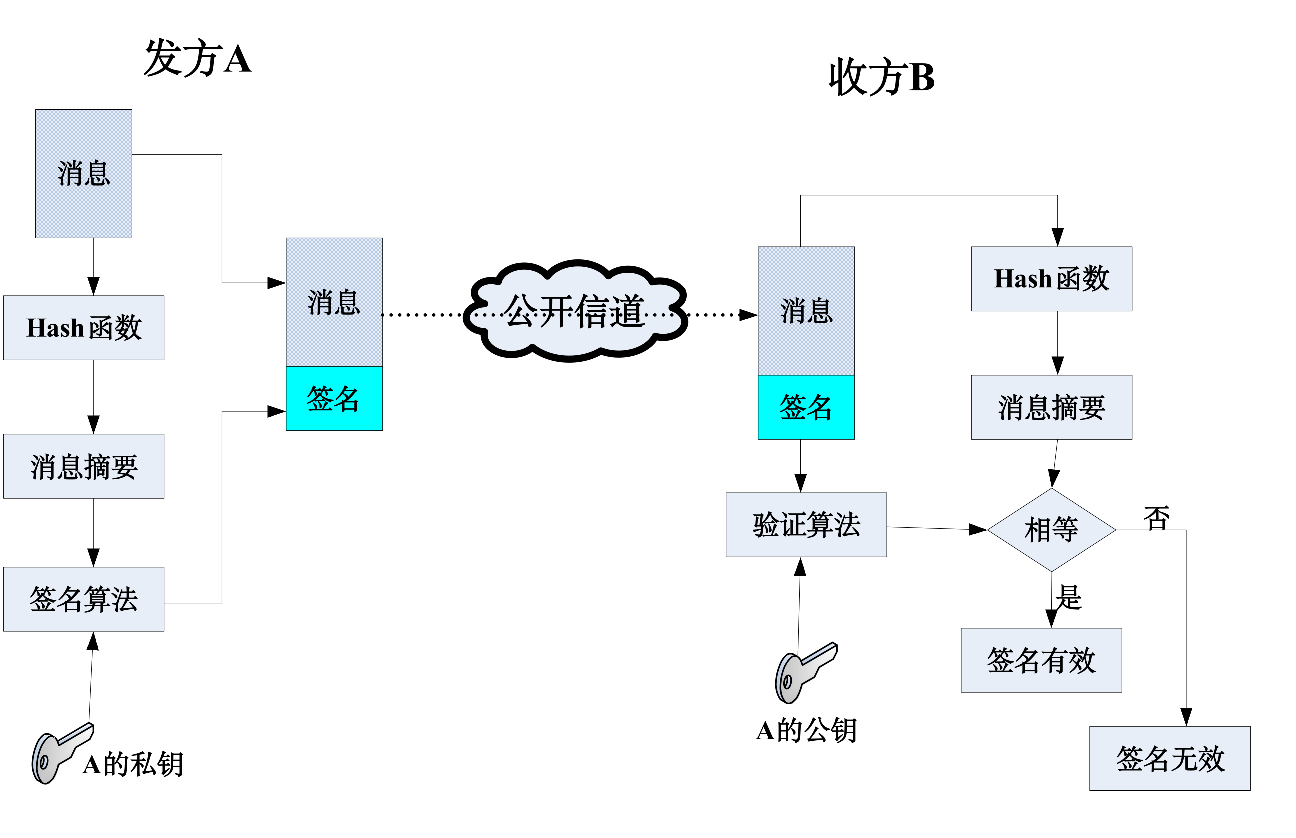
65.代理签名
代理签名是指原始签名者把他的签名权授权给代理者,代理者代表原始签名者行使他的签名权。当验证者验证代理签名时,验证者既能验证这个签名的有效性,也能确信这个签名是原始签名者认可的签名。
代理签名按照原始签名者给代理签名者的授权形式可分为完全委托的代理签名、部分授权的代理签名(非保护代理者的代理签名、保护代理者的代理签名)、带授权书的代理签名
66.盲签名
盲签名是D.Chaum于1982年首次提出的一种具有特殊性质的数字签名,这种签名要求签名者能够在不知道被签名文件内容的情况下对消息进行签名。
即使签名者在以后看到了被签名的消息及其签名,签名者也不能判断出这个签名是他何时为谁生成的。直观上讲,这种签名的生成过程就像签名者闭着眼睛对消息签名一样,所以形象地称为“盲”数字签名。
67.多重数字签名
在数字签名应用中,有时需要多个用户对同一文件进行签名和认证。能够实现多个用户对同一文件进行签名的数字签名方案称为多重数字签名(Digital Multi-signature)方案。
68.群签名
1991年,Chaum和Heyst首次提出群签名(Group Signature)(组签名)方案。群签名方案允许组中合法用户以用户组的名义签名,具有签名者匿名,只有权威者才能辨认签名者身份等多个特点。一般来说,群签名的参与者由群成员(签名者)、**群管理员(GC,Group Center)和签名接受者(签名验证者)**组成。
69.不可否认签名
不可否认签名本质的是在无签名者合作条件下不可能验证签名的有效性,从而可以防止他所签文件的复制或散布,这一性质使签名者可以控制产品的散发,在电子出版系统和知识产权保护中有所应用。
八、密码协议
70.密码协议
协议是指双方或多方为完成一项任务所进行的一系列步骤,而每一步必须依次执行,在前一步完成之前,后面的步骤都不能执行。
密码协议是以密码算法(包括对称密码算法、公钥密码算法、散列函数等)为基础完成某项任务并且满足安全需求的协议,也称作安全协议。常见的密码协议包括:密钥建立协议、认证协议、零知识证明协议、比特承诺、安全多方计算协议等。
71.参与者
参与者指参与协议的各方,每个参与者被抽象为具有概率多项式时间算法的图灵机.参与者可能是朋友或完全信任的人,也可能是敌人或相互完全不信任的人。据参与者在协议中的行为将其分为:诚实参与者、半诚实参与者和恶意参与者。
72.诚实参与者
诚实参与者完全按照要求完成执行过程中的各个步骤,同时保密自己的所有输入、输出及中间结果。诚实参与者也会根据自己的输入、输出以及中间结果来推导其他参与者的信息,但是不会被攻击者腐败。
73.半诚实参与者
半诚实参与者在协议的执行过程中,完全按照协议的要求完成协议的各个步骤,但同时可能将自己的输入、输出及中间结果泄露给攻击者。
74.恶意参与者
恶意参与者在协议的执行过程中,完全按照攻击者的意志执行协议的各个步骤,他不但将自己的所有输入、输出及中间结果泄露给攻击者,还可以根据攻击者的意图改变输入信息、伪造中间及输出信息,甚至中止协议。
75.攻击者
协议执行中,攻击者会破坏协议安全性或正确性,通过腐败参与者的一个子集,来控制其对协议进行攻击。根据攻击者对恶意参与者的控制程度、攻击者的计算能力、对恶意参与者的控制程度、网络同步与异步状态、自适应性等准则,可以对攻击者有不同的分类。其中按照对恶意参与者的控制程度,可以将攻击者分为以下下三类:
76.被动攻击者
被动攻击者又称为半诚实攻击者,只是监听恶意参与者的输入、输出及中间计算结果,并不控制恶意参与者的行为(比如修改恶意参与者的输入输出)。
77.主动攻击者
除了监听任意参与者的输入、输出及中间结果外,主动攻击者还控制恶意参与者的行为(如恶意篡改参与者的输入,按照自己的意图控制恶意参与者的输出等)。
78.隐蔽攻击者
隐蔽攻击者(Convert adversary)指介于被动攻击者与主动攻击者之间的攻击者类型,隐蔽攻击者以被发现的概率为(称为遏制因子)危险去攻击协议,被隐蔽攻击者腐败的参与者可以进行主动的腐败行为。
79.半诚实模型
如果所有参与者都是半诚实或诚实的,称此模型为半诚实模型。半诚实成员完全遵守协议,但它会收集协议执行过程中的所有记录,并试图推断其他成员的输入,半诚实模型中的攻击者都是被动的。
80.恶意模型
有恶意参与者的模型称为恶意模型。恶意参与者完全按照攻击者的意愿执行协议的各个步骤,他不但将自己的所有输入、输出以及中间结构泄露给攻击者,还可以根据攻击者的意图改变改变输入信息、伪造中间及输出信息,甚至终止协议。恶意模型中的攻击者是主动的。
81.隐蔽攻击模型
有被隐蔽攻击者参与的模型称为隐蔽攻击者模型,被腐败的参与者可以进行主动的腐败行为,但仅在能小于一定概率不被发现的情况下才可实施腐败行为。
82.零知识证明
零知识证明(Zero Knowledge Proof)由S.Goldwasser、S.Micali 及 C.Rackoff于1985年在论文《The Knowledge Complexity of Interactive Proof Systems》(交互式证明系统中的知识复杂性)首次提出,是一种用于证明者在不泄露任何其他信息的情况下证明其掌握知识正确性的密码学协议。
该协议的一方称为证明者(Prover),用 P P P表示;另一方称为验证者(Verifier),用 V V V表示。零知识证明指 P P P试图使 V V V相信某个论断是正确的,但却不向 V V V泄露任何有用的信息,即 P P P在论证的过程中 V V V得不到任何有用的信息。零知识证明除了证明证明者论断的正确性外不泄露任何其他信息或知识。
83.安全多方计算
安全多方计算问题SMC,Secure Multi-party Computation)由由中国计算机科学家、2000年图灵奖获得者姚启智教授于1982年在论文《Protocols for secure computations》中以百万富翁问题(两个百万富翁Alice和Bob想知道他们两个谁更富有,但他们都不想让对方及其他第三方知道自己财富的任何信息),开创了密码学研究的新领域。
安全多方计算是指在一个互不信任的多用户网络中, n n n个参与者 P 1 , P 2 , . . . , P n P_1,P_2,...,P_n P1,P2,...,Pn,每个持有秘密数据 x i x_i xi,希望共同计算出函数 f ( x 1 , x 2 , . . . , x n ) = ( y 1 , y 2 , . . . , y n ) f(x_1,x_2,...,x_n)=(y_1,y_2,...,y_n) f(x1,x2,...,xn)=(y1,y2,...,yn), P i P_i Pi仅得到结果 y i y_i yi,并且不泄露 x i x_i xi给其他参与者。
九、密钥管理
84.密钥管理
密钥管理就是在授权各方之间实现密钥关系的建立和维护的一整套技术和程序,涉及密钥从产生到最终销毁的整个过程,包括密钥的生成、存储、分发与协商、使用、备份与恢复、更新、撤销和销毁等。
85.会话密钥
会话密钥(Session Key)主要用于对两个通信终端用户的交换数据进行加密,也称数据加密密钥(Data Encrypting Key)。会话密钥的生存周期非常短,通常在会话建立初生成,在会话结束后销毁,主要用来对传输的数据进行保护。会话密钥大多数是临时的、动态生成的,可由通信双方协商得到,也可由密钥分配中心分配。
86.密钥加密密钥
密钥加密密钥(Key Encrypting Key)主要用于对要传送的会话密钥进行加密,也称为二级密钥(SecondaryKey)、次主密钥或辅助密钥。密钥加密密钥的生存周期相对较长,由于它主要用来协商或传送会话密钥,一旦泄露可导致在其使用周期内的所有会话密钥泄露。
87.主密钥
主密钥(Master Key)主要用于对密钥加密密钥或会话密钥的保护,使得这些密钥可以实现在线分发。主密钥对应于层次化密钥结构中的最高层次,它是由用户选定或由系统分配给用的、可在较长时间内由用户所专有的秘密密钥,在某种程度上,主密钥还起到标识用户的作用。它的生存周期最长,受到严格的保护。
88.密钥生命周期
密钥的生命周期是指密钥从产生到最终销毁的整个过程。在这个生命周期中,密钥处于4种不同的状态中:使用前状态(密钥不能用于正常的密码操作)、使用状态(密钥是可用的,并处于正常使用中)、使用后状态(密钥不再正常使用,但为了某种目的对其进行离线访问是可行的)、过期状态(密钥不再使用,所有的密钥记录已被删除)
89.密钥分发
通过密钥分发机制,通信双方中的一方或密钥分配中心选取一个秘密密钥,在不让其他人(除密钥分配中心)看到密钥的情况下,将其传送给通信双方中的另一方。为防止攻击者得到密钥,须时常更新密钥,密码系统的强度依赖于密钥分配技术。
90.密钥协商
密钥协商目的是通信双方在网络中通过交换信息来生成一个双方共享的会话密钥。典型的密钥协议是Diffie-Hellrman密钥交换协议,该协议是一个无身份认证要求的双方密钥协商方案,在这个协议基础上改进的端对端协议(Station-to-Station Pratocol)是一个更安全的密钥协商协议。
91.密钥托管
密钥托管也称为托管加密,是指为公众和用户提供更好安全通信的同时,也允许授权者(包括政府保密部门、企业专门技术人员和特殊用户等)为了国家、集团的利益监听某些通信内容并能解密相关密文。密钥托管也叫“密钥恢复”,或者理解为“受信任的第三方”“数据恢复”和“特殊获取”等含义,对个人没有绝对的隐私和绝对不可跟踪的匿名性。其实现手段是把已加密的数据和数据恢复密钥联系起来,数据恢复密钥不必是直接解密的密钥,但由它可得解密密钥。
92.托管加密标准
为有效控制密码技术的使用,美国政府于1993年4月提出Clipper计划和密钥托管加密技术。密钥托管技术的实质是建议联邦政府和工业界使用新的具有密钥托管功能的联邦加密标准,即托管加密标准(EES,Escrowed Encryption Standard),又称Clipper建议。EES标准于1994年2月正式被美国政府公布采用。EES标准的核心是由美国国家安全局(NSA)主持开发的软硬件实现的密码部件,称为Clipper的防窜扰芯片。
93.公钥基础设施
公钥基础设施(PKI,Public Key Infrastructure)是基于公钥密码学的,提供安全服务的基础设施,核心是要解决信息网络空间中的信任问题,确定可信赖的数字身份。
PKI技术以公钥技术为基础,以数字证书为媒介,结合对称加密和非对称加密技术,将个人、组织、设备的身份标识信息与各自的公钥捆绑在一起,其主要目的是通过自动管理密钥和证书,为用户建立起一个安全可信的网络运行环境,使用户可以在多种应用环境下方便地使用加密和数字签名技术,保证传输信息的机密性、完整性、认证性和不可否认性,广泛应用于电子商务、电子政务等领域。
94.CA
认证机构CA(Certificate Authority),又称证书授证中心,是PKI的核心组成部分和执行机构,它为每个使用公钥的用户发放一个数字证书,证明证书中列出的用户合法拥有证书中列出的公开密钥。认证中心还应包括证书申请注册机构RA(Registration Authority),它是数字证书的注册审批机构。
95.数字证书
数字证书也称公钥证书,是一个经权威机构认证中心CA签名的包含了公钥及公钥持有者身份信息的文件,相当于CA颁发的“身份证”,解决“公钥属于谁”的问题,帮助用户安全地获得对方公钥。
数字证书内容包括:版本号(区分x.509的不同版本)、序列号(CA给予每一个证书的分配惟一的数字标识)、认证机构标识(颁发该证书的机构惟一的CA的X.500名字)、主体标识(证书持有者的名称)、主体公钥信息(和该主体私钥相对应的公钥)、证书有效期等信息。
96.证书链
在PKI的应用中,用户的信任来源于对证书的验证,而这种信任是基于对颁发证书可信第三方CA本身的信任。X.509规定CA用目录信息树(DIT)的方式组织。最高一级CA称为根CA(Root-CA),用户之间的证书验证,需要对方证书生成的一条链(证书链)才能进行。由根证书为起点,透过层层信任(A信任B,B信任C,以此类推),使终端实体证书的持有者可以获得转授的信任,以证明身份。
97.时间戳权威
由于用户桌面时间很容易改变,由该时间产生的时间戳不可信赖,因此需要一个可信任的第三方来提供可信赖的且不可抵赖的时间戳服务。时间戳权威(TSA,Time StampAuthority),它是PKI中的重要组成部分,作为可信的第三方时间权威,其主要功能是提供可靠的时间信息,证明某份文件(或某条信息)在某个时间(或以前)存在,防止用户在这个时间前或时间后伪造数据进行欺骗活动。
98.数字信封
数字信封是一种利用对称加密技术和非对称加密技术两者的优点进行信息安全传输的一种技术,数字信封既发挥了对称加密算法速度快、安全性好的优点,又发挥了非对称加密算法密钥管理方便的优点。
数字信封使用会话密钥加密需要传输的消息,并用接受者的公钥加密会话密钥。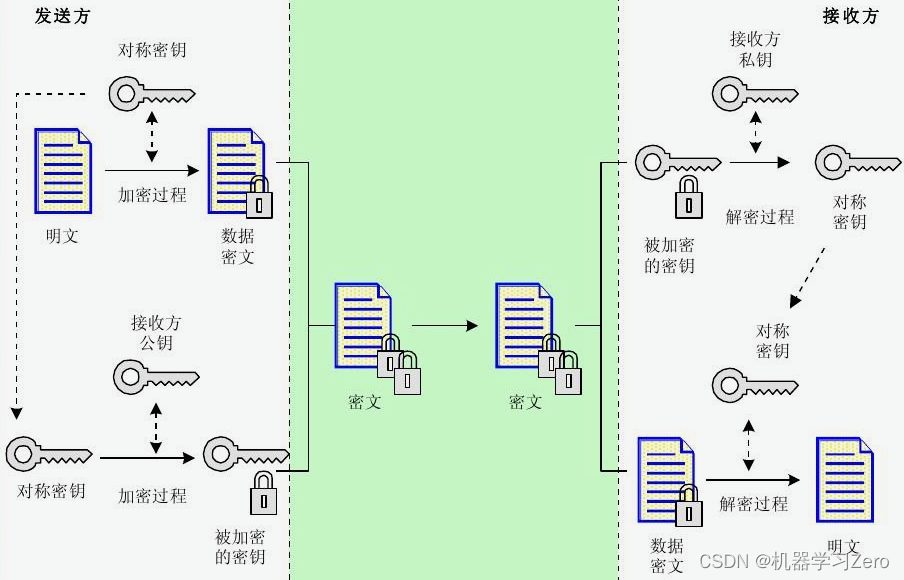
十、量子密码
99.量子密码
量子密码学是量子物理学和密码学相结合的一门新兴科学,量子密码通信不是用来传送密文或明文,而是用来建立和传送密钥的,这个密钥是绝对安全的。量子密码通信是目前科公认唯一能实现绝对安全的通信方式,能够保证合法的通信双方可觉察潜在的窃听者并采取相应的措施使窃听者无法破解量子密码,无论破译者有多么强大的计算能力。
量子密码是利用量子的不确定性,构造安全的通信通道,使得通信双方能够检测到信息是否被窃听,这一性质为通信双方提供密钥协商或密钥交换时的绝对安全。量子加密学不依赖问题的计算难度,而使用基本的物理定律提供了可证的无条件安全。并且不同于一次一密的密钥,任何窃听量子密钥交换和复制密钥的人不可能不被检测到。
量子密码的安全性基于量子力学的海森堡(Heisenberg)的测不准原理(Uncertainty Principle),因此要攻破量子密码协议就意味着必须否定量子力学定律,所以量子密码是理论上安全的密码技术。
100.量子密码系统
量子密码系统就是使得发送方用量子信道与接收方共享秘密信息,而未经授权的第三方无法窃取信息的密码系统。一个量子密码系统由量子信源、量子信道、经典信道、发送方、接收方等部分组成。