秘密共享
1. 秘密共享简介2. Shamir秘密共享方案3. Asmuth-Bloom方案4. 可验证的秘密共享4.1 Feldman的VSS方案4.2 Pedersen的VSS方案 5. 无分发者的随机秘密共享
1. 秘密共享简介
秘密共享通过将秘密以适当的方式拆分,拆分后的每一个份额由不同的参与者管理,单个参与者无法恢复秘密信息,只有若干个参与者一同协作才能恢复秘密消息。
秘密共享定义如下:秘密持有者 S S S需要将原始秘密 m m m在参与者集合中 P 1 , P 2 , . . . , P n P_1,P_2,...,P_n P1,P2,...,Pn分享, S S S分发给 P 1 P_1 P1子秘密 m p i m_{p_i} mpi,使得只有特定参与者的集合才能够从他们的子秘密中恢复秘密 m m m,而其他参与者不能得到秘密 m m m的任何信息。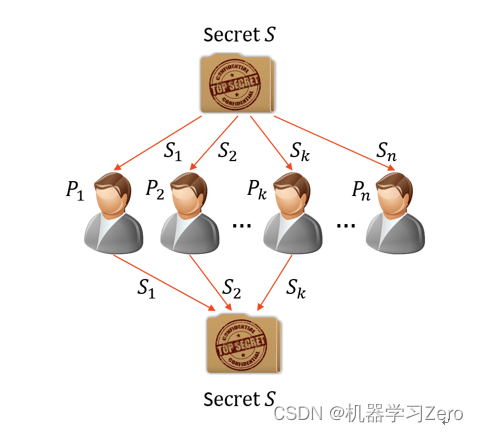
能够计算出秘密 m m m的参与者集合 P P P的一个子集 A ⊆ P A \subseteq P A⊆P,称为一个授权子集。令 Γ \Gamma Γ为所有授权子集构成的集合,则称 Γ \Gamma Γ访问结构。
秘密共享方案一般描述如下:将共享的秘密 m m m分割成 n n n个子秘密,并将其分发至 n n n个参与者,使得授权子集 Γ \Gamma Γ中的参与者可共同恢出复秘密 m m m,而非授权子集中的参与者无法得到关于秘密 m m m的任何信息。
2. Shamir秘密共享方案
Adi Shamir于1979年提出了基于拉格朗日(Lagrange)插值定理的 ( t , n ) (t,n) (t,n)-门限方案。该方案利用有限域上的次随机多项式来分享秘密,被分享的秘密为多项式的零次系数,恢复秘密至少需要t个多项式上的点。
方案描述如下:
设 G F ( q ) G F(q) GF(q) 是一个有限域, q q q为公开大素数, 共享的密钥 k ∈ G F ( q ) k \in G F(q) k∈GF(q), 可信中心给 n ( n < q ) n(n< q) n(n<q)个共享者 P i ( 1 ≤ i ≤ n ) P_i(1 \leq i \leq n) Pi(1≤i≤n) 分配共享的过程如下:
(1) 秘密分发
可信中心随机选取多项式 f ( x ) = a t − 1 x t − 1 + … + a 2 x 2 + a 1 x + a 0 ∈ f(x)=a_{t-1} x^{t-1}+\ldots+a_2 x^2+a_1 x+a_0 \in f(x)=at−1xt−1+…+a2x2+a1x+a0∈ G F ( q ) [ x ] G F(q)[x] GF(q)[x], 常数 a 0 = k a_0=k a0=k 为要分享的秘密。
可信中心在 G F ( q ) G F(q) GF(q) 中选择 n n n 个非零的互不相同的 元素 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn, 计算 y i = f ( x i ) , 1 ≤ i ≤ n y_i=f\left(x_i\right), 1 \leq i \leq n yi=f(xi),1≤i≤n, 将子密钥 ( x i , y i ) \left(x_i, y_i\right) (xi,yi) 分配给共享者 P i ( x i P_i\left(x_i\right. Pi(xi 是公开的, y i y_i yi 为 P i P_i Pi 的秘密共享)。
(2) 秘密重构
给定 t t t 个共享 y i s ( 1 ≤ s ≤ t ) y_{i_s}(1 \leq s \leq t) yis(1≤s≤t), 从Lagrange多项式重构的
f ( x ) = ∑ s = 1 t y i s ∏ j = 1 , j ≠ s t x − x j x i s − x i j , k = a 0 = f ( 0 ) = ∑ s = 1 t y i s ∏ j = 1 , j ≠ s t − x j x i s − x i j = ∑ s = 1 t b s y i s , \begin{aligned} & f(x)=\sum_{s=1}^t y_{i_s} \prod_{j=1, j \neq s}^t \frac{x-x_j}{x_{i_s}-x_{i_j}}, \\ & k=a_0=f(0)=\sum_{s=1}^t y_{i_s} \prod_{j=1, j \neq s}^t \frac{-x_j}{x_{i_s}-x_{i_j}}=\sum_{s=1}^t b_s y_{i_s}, \end{aligned} f(x)=s=1∑tyisj=1,j=s∏txis−xijx−xj,k=a0=f(0)=s=1∑tyisj=1,j=s∏txis−xij−xj=s=1∑tbsyis,其中, b s = Π j = 1 , j ≠ s t − x j x i s − x i j b_s=\Pi_{j=1, j \neq s}^t \frac{-x_j}{x_{i_s}-x_{i_j}} bs=Πj=1,j=stxis−xij−xj (Lagrange插值系数), 运算都是 G F ( q ) G F(q) GF(q)上的运算。
Eg 设 t = 3 , n = 5 , q = 9 , k = 11 t=3, n=5, q=9, k=11 t=3,n=5,q=9,k=11, 随机选取 a 1 = 2 , a 2 = 7 a_1=2, a_2=7 a1=2,a2=7, 得多项式为 h ( x ) = ( 7 x 2 + 2 x + 71 ) m o d 19 h(x)=\left(7 x^2+2 x+71\right) \bmod 19 h(x)=(7x2+2x+71)mod19选择 x i = i x_i=i xi=i, 则由 y i = h ( x i ) , 1 ≤ i ≤ 5 y_i=h\left(x_i\right), \quad 1 \leq i \leq 5 yi=h(xi),1≤i≤5, 很容易得到 5 5 5个子密钥 h ( 1 ) = 1 , h ( 2 ) = 5 , h ( 3 ) = 4 , h ( 4 ) = 17 , h ( 5 ) = 6 h(1)=1, h(2)=5, h(3)=4, h(4)=17, h(5)=6 h(1)=1,h(2)=5,h(3)=4,h(4)=17,h(5)=6如果知道其中 3 个子密钥 h ( 2 ) = 5 , h ( 3 ) = 4 , h ( 5 ) = 6 h(2)=5, h(3)=4, h(5)=6 h(2)=5,h(3)=4,h(5)=6 { 4 a 2 + 2 a 1 + a 0 = 5 9 a 2 + 3 a 1 + a 0 = 4 25 a 2 + 5 a 1 + a 0 = 6 \begin{cases} 4 a_2+2 a_1+a_0=5 \\ 9 a_2+3 a_1+a_0=4 \\ 25 a_2+5 a_1+a_0=6\end{cases} ⎩ ⎨ ⎧4a2+2a1+a0=59a2+3a1+a0=425a2+5a1+a0=6从而解得 k = a 0 = 11 k=a_0=11 k=a0=11。
3. Asmuth-Bloom方案
Asmuth和Bloom于1980年提出了一个基于中国剩余定理的 ( t , n ) (t,n) (t,n)-门限方案。该方案中,成员的共享是由秘密 S S S 得出的数 y y y 对于不同模数 m 1 , m 2 , … , m n m_1, m_2, \ldots, m_n m1,m2,…,mn 的剩余。
令 p , d 1 , d 2 , … , d n p, d_1, d_2, \ldots, d_n p,d1,d2,…,dn 是满足下列条件的一组正整数: p > k ; d 1 < d 2 < … < d n p>k ; \quad d_1<d_2<\ldots<d_n p>k;d1<d2<…<dn对所有的 i , gcd ( p , d i ) = 1 ; i, \operatorname{gcd}\left(p, d_i\right)=1 ; i,gcd(p,di)=1;
对 i ≠ j , gcd ( d i , d j ) = 1 ; d 1 d 2 ⋯ d t > i \neq j, \operatorname{gcd}\left(d_i, d_j\right)=1 ; d_1 d_2 \cdots d_t> i=j,gcd(di,dj)=1;d1d2⋯dt> p d n − t + 2 d n − t + 3 ⋯ d n p d_{n-t+2} d_{n-t+3} \cdots d_n pdn−t+2dn−t+3⋯dn
令 N = d 1 d 2 ⋯ d t N=d_1 d_2 \cdots d_t N=d1d2⋯dt 是 t t t 个最小整数之积,则 N / p N / p N/p 大于任意 t − 1 t-1 t−1 个 d i d_i di 。令 r r r 是区间 [ 0 , ⌊ N / p ⌋ − 1 ] [0,\lfloor N / p\rfloor-1] [0,⌊N/p⌋−1] 中的一个随机整数, 并公布 p , r p, r p,r 。
(1) 秘密分发
将 k k k 划分为 n n n 个共享, 计算 k ′ = k + r p k^{\prime}=k+r p k′=k+rp, 则 k ′ ∈ [ 0 , N − 1 ] 。 n k^{\prime} \in[0, N-1] 。 n k′∈[0,N−1]。n 个共享 为 k i = k ′ modd i , i = 1 , 2 , … , n k_i=k^{\prime} \operatorname{modd}_i, i=1,2, \ldots, n ki=k′moddi,i=1,2,…,n, 将子密钥 ( d i , k i ) \left(d_i, k_i\right) (di,ki) 分配给共享者 P i ( d i P_i\left(d_i\right. Pi(di 是公开的, k i k_i ki 为 P i P_i Pi
(2) 秘密重构
若给定 t t t 个共享 k i 1 , … , … , k i t k_{i_1}, \ldots, \ldots, k_{i_t} ki1,…,…,kit, 则由中国剩余定理可知, 同余方程组 { x ′ ≡ k i 1 mod d i 1 x ′ ≡ k i 2 mod d i 2 ⋯ x ′ ≡ k i t mod d i t \begin{cases} x^{\prime} \equiv k_{i_1} \operatorname{mod} d_{i_1} \\ x^{\prime} \equiv k_{i_2} \operatorname{mod} d_{i_2} \\ \cdots \\ x^{\prime} \equiv k_{i_t} \operatorname{mod} d_{i_t} \end{cases} ⎩ ⎨ ⎧x′≡ki1moddi1x′≡ki2moddi2⋯x′≡kitmoddit关于模 N 1 = d i 1 d i 2 ⋯ d i t N_1=d_{i_1} d_{i_2} \cdots d_{i_t} N1=di1di2⋯dit 在 [ 0 , N 1 − 1 ] \left[0, N_1-1\right] [0,N1−1] 内有唯一解 x x x, 因为 N 1 ≥ N ≥ k ′ N_1 \geq N \geq k^{\prime} N1≥N≥k′, 推出 k ′ = x k^{\prime}=x k′=x 。 最后计算出 k = k ′ − r p k=k^{\prime}-r p k=k′−rp, 即 k = k ′ m o d p k=k^{\prime} \bmod p k=k′modp 。
Eg 设 t = 2 , n = 3 , p = 7 , k = 4 , d 1 = 9 , d 2 = 11 , d 3 = 13 t=2, n=3, p=7, k=4, d_1=9, d_2=11, d_3=13 t=2,n=3,p=7,k=4,d1=9,d2=11,d3=13, 则 N = d 1 d 2 = 99 > 91 = 7 ⋅ 13 = p ⋅ d 3 . N=d_1 d_2=99>91=7 \cdot 13=p \cdot d_3 . N=d1d2=99>91=7⋅13=p⋅d3.在 [ 0 , [ 99 / 7 ] − 1 ] = [ 0 , 13 ] [0,[99 / 7]-1]=[0,13] [0,[99/7]−1]=[0,13] 之间随机取 r = 10 , k ′ = k + r p = 4 + 10 × 7 = 74 r=10, k^{\prime}=k+r p=4+10 \times 7=74 r=10,k′=k+rp=4+10×7=74, k 1 ≡ k ′ modd d 1 ≡ 74 m o d 9 ≡ 2 k 2 ≡ k ′ m o d d 2 ≡ 74 m o d 11 ≡ 8 k 3 ≡ k ′ m o d d 3 ≡ 74 m o d 13 ≡ 9 \begin{aligned} & k_1 \equiv k^{\prime} \text { modd } d_1 \equiv 74 \bmod 9 \equiv 2 \\ & k_2 \equiv k^{\prime} \bmod d_2 \equiv 74 \bmod 11 \equiv 8 \\ & k_3 \equiv k^{\prime} \bmod d_3 \equiv 74 \bmod 13 \equiv 9\end{aligned} k1≡k′ modd d1≡74mod9≡2k2≡k′modd2≡74mod11≡8k3≡k′modd3≡74mod13≡93 个子密钥为 { ( 9 , 2 ) , ( 11 , 8 ) , ( 13 , 9 ) } \{(9,2),(11,8),(13,9)\} {(9,2),(11,8),(13,9)}。
若知道 { ( 9 , 2 ) , ( 11 , 8 ) } \{(9,2),(11,8)\} {(9,2),(11,8)}, 可建立方程组: { k ′ ≡ 2 mod 9 k ′ ≡ 8 mod 11 \begin{cases} k^{\prime} \equiv 2 \operatorname{mod} 9 \\ k^{\prime} \equiv 8 \operatorname{mod} 11 \\\end{cases} {k′≡2mod9k′≡8mod11根据中国剩余定理,解得: k ′ ≡ ( 11 × 5 × 2 + 9 × 5 × 8 ) m o d ≡ 74 k^{\prime} \equiv(11 \times 5 \times 2+9 \times 5 \times 8) \bmod \equiv 74 k′≡(11×5×2+9×5×8)mod≡74因此 k ′ ≡ k m o d p = 4 k^{\prime} \equiv k \bmod p=4 k′≡kmodp=4
4. 可验证的秘密共享
可验证的秘密共享VSS方案是对传统秘密共享方案的修正,在通常的秘密分享方案基础上附加验证操作构成,主要用于解决不诚实的分发中心问题。
在VSS方案中,分发者不但分发秘密的碎片,而且广播对秘密碎片的承诺,当个成员收到其碎片时,要验证其碎片是否正确;在秘密重构阶段,每个参与者也采用同样方法验证其他成员秘密碎片的正确性。
VSS主要抵抗以下两种主动攻击:
分发者在秘密分发协议中发送错误碎片给部分或全部参与者。协议参与者在秘密重构协议中提交错误碎片。常见的可验证的秘密共享方案包括Feldman的VSS方案以及Pedersen方案。
4.1 Feldman的VSS方案
(1)秘密分发
可信中心选取阶随机多项式: f ( x ) = a t − 1 x t − 1 + … + a 2 x 2 + a 1 x + a 0 ∈ G F ( q ) [ x ] f(x)=a_{t-1} x^{t-1}+\ldots+a_{2} x^{2}+a_{1} x+a_{0} \in G F(q)[x] f(x)=at−1xt−1+…+a2x2+a1x+a0∈GF(q)[x]常数 a 0 = s a_{0}=s a0=s为要分发的秘密;
可信中心选择 n n n个非零的互不相同的元素 x 1 , x 2 , … , x n ∈ G F ( q ) x_{1}, x_{2}, \ldots, x_{n} \in G F(q) x1,x2,…,xn∈GF(q),计算 y i = f ( x i ) , 1 ≤ i ≤ n y_{i}=f\left(x_{i}\right), 1 \leq i \leq n yi=f(xi),1≤i≤n , 将子密钥 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 分配给共享者 P i P_{i} Pi( ( x i ) \left(x_{i}\right) (xi)是公开的, y i y_{i} yi为 P i P_{i} Pi的秘密共享),可信中心计算并广播承诺 B j = g a j , 0 ≤ j < t B_{j}=g^{a_{j}}, 0 \leq j<t Bj=gaj,0≤j<t。
参与者 P i P_{i} Pi收到自己的碎片 y i y_{i} yi后, 判断 g y i = Π j = 0 t − 1 B j x i j g^{y_{i}}=\Pi_{j=0}^{t-1} B_{j}^{x_{i}^{j}} gyi=Πj=0t−1Bjxij是否成立, 如果成立, 则接受该 碎片为有效; 否则, P i P_{i} Pi 请求可信中心重新发送正确的碎片。
若可信中心向 P i P_{i} Pi 传送了正确的碎片 y i y_{i} yi, 则有 g y i = g f ( x i ) = g a t − 1 r i t − 1 + … + a 2 x i 2 + a 1 x i + a 0 = g a t − 1 x i t − 1 … g a 2 x i 2 g a 1 x i g a 0 = B t − 1 x i t − 1 … B 2 x i 2 B 7 x i B 0 = Π j = 0 t − 1 B j x i j \begin{aligned} g^{y_{i}=g^{f\left(x_{i}\right)}} & =g^{a_{t-1} r_{i}^{t-1}+\ldots+a_{2} x_{i}^{2}+a_{1} x_{i}+a_{0}} \\ & =g^{a_{t-1} x_{i}^{t-1}} \ldots g^{a_{2} x_{i}^{2}} g^{a_{1} x_{i}} g^{a_{0}} \\ & =B_{t-1}^{x_{i}^{t-1}} \ldots B_{2}^{x_{i}^{2}} B_{7}^{x_{i}} B_{0} \\ & =\Pi_{j=0}^{t-1} B_{j}^{x_{i}^{j}} \end{aligned} gyi=gf(xi)=gat−1rit−1+…+a2xi2+a1xi+a0=gat−1xit−1…ga2xi2ga1xiga0=Bt−1xit−1…B2xi2B7xiB0=Πj=0t−1Bjxij(2)秘密重构
假设每个参与者都接受到正确的碎片, 他们中的任意 t t t个可执行 Shamir门限秘密分享方案中的重构算法恢复出院时秘密, 即 P i P_{i} Pi向参与重构的其他人广播自己的碎片,这样每个参与重构的成员均可验证所接收到的碎片的有效性,然后使用Lagrange揷值公式计算出秘密 S S S。
Feldman的VSS方案中, 由于可信中心在广播承诺时将 B 0 = g a 0 = g s B_{0}=g^{a_{0}}=g^{s} B0=ga0=gs也作为一个承诺发出, 因此方案仅是计算安全的。
4.2 Pedersen的VSS方案
Pedersen扩展了Feldman的方案,将Shamir秘密共享方案与承诺方案相结合,构造出了一个高效、安全的非交互式可验证秘密共享方案,且验证信息不会直接泄露秘密 k k k,因此是信息论安全的。
(1)秘密分发
可信中心选取两个 t t t阶随机多项式: a ( x ) = a t − 1 x t − 1 + … + a 2 x 2 + a 7 x + a 0 ∈ G F ( q ) [ x ] b ( x ) = b t − 1 x t − 1 + … + b 2 x 2 + b 1 x + b 0 ∈ G F ( q ) [ x ] \begin{array}{l} a(x)=a_{t-1} x^{t-1}+\ldots+a_{2} x^{2}+a_{7} x+a_{0} \in G F(q)[x] \\ b(x)=b_{t-1} x^{t-1}+\ldots+b_{2} x^{2}+b_{1} x+b_{0} \in G F(q)[x] \end{array} a(x)=at−1xt−1+…+a2x2+a7x+a0∈GF(q)[x]b(x)=bt−1xt−1+…+b2x2+b1x+b0∈GF(q)[x]常数 a 0 = s a_{0}=s a0=s为要分发的秘密。
可信中心选择 n n n个非零的互不相同的元素 x 1 , x 2 , … , x n ∈ G F ( q ) x_{1}, x_{2}, \ldots, x_{n} \in G F(q) x1,x2,…,xn∈GF(q) ,计算 y i = ( s i , s i 2 ) = ( a ( x i ) , b ( x i ) ) , 1 ≤ i ≤ n y_{i}=\left(s_{i}, s_{i 2}\right)=\left(a\left(x_{i}\right), b\left(x_{i}\right)\right), 1 \leq i \leq n yi=(si,si2)=(a(xi),b(xi)),1≤i≤n 将子密钥 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi)分配给共享者 P i P_{i} Pi( x i x_{i} xi是公开的, y i y_{i} yi为 P i P_{i} Pi的秘密共享)。可信中心计算并广播承诺 C j = g a j h b j , 0 ≤ j < t C_{j}=g^{a_{j}} h^{b_{j}}, 0 \leq j<t Cj=gajhbj,0≤j<t 。
参与者 P i P_{i} Pi 收到自己的碎片 y i y_{i} yi 后, 判断 g s i ⌝ h s i 2 = ∏ j = 0 t − 1 C j x i j g^{s_{i\urcorner}} h^{s_{i 2}}=\prod_{j=0}^{t-1} C_{j}^{x_{i}^{j}} gsi┐hsi2=∏j=0t−1Cjxij 是否成立。如果成立, 则接受 该碎片为有效; 否则, P i P_{i} Pi 请求可信中心重新发送正确的碎片。
若可信中心向 P i P_{i} Pi传送了正确的碎片 y i y_{i} yi, 则有 g s i ⌝ h s i 2 = g a ( x i ) h b ( x i ) = ( g a t − 1 x i t − 1 + … + a 2 x i 2 + a 1 x i + a 0 ) ( h b t − 1 x i t − 1 + … + b 2 x i 2 + b 1 x i + b 0 ) = ( g a t − 1 h b t − 1 ) x i t − 1 … ( g a 2 h b 2 ) x i 2 ( g a a h b 1 ) x i g a 0 h b 0 = C t − 1 x i t − 1 … C 2 x i 2 C 1 x i C 0 = ∏ j = 0 t − 1 C j x i j \begin{aligned} g^{s_{i\urcorner}} h^{s_{i 2}}= & g^{a\left(x_{i}\right)} h^{b\left(x_{i}\right)}=\left(g^{a_{t-1} x_{i}^{t-1}+\ldots+a_{2} x_{i}^{2}+a_{1} x_{i}+a_{0}}\right)\left(h^{b_{t-1} x_{i}^{t-1}+\ldots+b_{2} x_{i}^{2}+b_{1} x_{i}+b_{0}}\right) \\ & =\left(g^{a} t-1 h^{b_{t-1}}\right)^{x_{i}^{t-1}} \ldots\left(g^{a_{2}} h^{b_{2}}\right)^{x_{i}^{2}}\left(g^{a^{a}} h^{b_{1}}\right)^{x_{i}} g^{a_{0}} h^{b_{0}} \\ & =C_{t-1}^{x_{i}^{t-1}} \ldots C_{2}^{x_{i}^{2}} C_{1}^{x_{i}} C_{0} \\ & =\prod_{j=0}^{t-1} C_{j}^{x_{i}^{j}} \end{aligned} gsi┐hsi2=ga(xi)hb(xi)=(gat−1xit−1+…+a2xi2+a1xi+a0)(hbt−1xit−1+…+b2xi2+b1xi+b0)=(gat−1hbt−1)xit−1…(ga2hb2)xi2(gaahb1)xiga0hb0=Ct−1xit−1…C2xi2C1xiC0=j=0∏t−1Cjxij(2)秘密重构
假设每个参与者都接受到正确的碎片, 他们中的任意 t t t个可执行 Shamir门限秘密分享方案中的重构算法恢复出院时秘密, 即 P i P_{i} Pi向参与重构的其他人广播自己的碎片, 这样每个参与重构的成员均可验证所接收到的碎片的有效性, 然后使用Lagrange揷值公式计算出秘密 s s s 。
Pedersen的VSS方案中,可信中心在广播承诺时与秘密 s s s相关的信息仅为 C 0 = g s h b 0 C_{0}=g^{s} h^{b_{0}} C0=gshb0,没有泄露关于 s s s的任何信息,因此方案是信息论安全的。
5. 无分发者的随机秘密共享
在该秘密体制中不存在秘密分发者,仅有参与者 P 1 , P 2 , . . . , P n P_1,P_2,...,P_n P1,P2,...,Pn,他们以交互的方式协商出一个随机秘密 s s s,并各自得到该秘密的一个碎片 s i s_i si,但每个参与者都不知道这个随机秘密的具体值,除非他们公布自己的碎片并重构该秘密。
基于Shamir的秘密分享体制的一个无秘密分发者的 ( t , n ) (t,n) (t,n)秘密分享体制,称为Joint-Shamir-RSS方案(Joint Shamir Random Secret Sharing)。
(1) 每个参与者 P i P_i Pi 选择一个 t − 1 t-1 t−1 次随机多项式 f i ( x ) = a i , t − 1 x t − 1 + … + a i 2 x 2 + a i 1 x + a i 0 ∈ G F ( q ) [ x ] f_i(x)=a_{i, t-1} x^{t-1}+\ldots+a_{i 2} x^2+a_{i1} x+a_{i0} \in G F(q)[x] fi(x)=ai,t−1xt−1+…+ai2x2+ai1x+ai0∈GF(q)[x], 以 a i 0 = f i ( 0 ) a_{i 0}=f_i(0) ai0=fi(0) 作为自己要让 P 1 , P 2 , … , P n P_1, P_2, \ldots, P_n P1,P2,…,Pn 分享的秘密。
(2) P i P_i Pi 计算 s i j = f i ( x j ) s_{ij}=f_i\left(x_j\right) sij=fi(xj), 发送给 P j , j = 1 , 2 , … , n P_j, j=1,2, \ldots, n Pj,j=1,2,…,n, 如下所示: P 1 P 2 P j P n P 1 f 1 ( x 1 ) f 7 ( x 2 ) f 7 ( x j ) f 1 ( x n ) P 2 f 2 ( x 1 ) f 2 ( x 2 ) f 2 ( x j ) f 2 ( x n ) P i f i ( x 1 ) f i ( x 2 ) f i ( x j ) f i ( x n ) P n f n ( x 1 ) f n ( x 2 ) f n ( x j ) f n ( x n ) \begin{array}{llllll} & P_1 & P_2 & P_j & P_n \\ P_1 & f_1\left(x_1\right) & f_7\left(x_2\right) & f_7\left(x_j\right) & f_1\left(x_n\right) \\ P_2 & f_2\left(x_1\right) & f_2\left(x_2\right) & f_2\left(x_j\right) & f_2\left(x_n\right) \\ P_i & f_i\left(x_1\right) & f_i\left(x_2\right) & f_i\left(x_j\right) & f_i\left(x_n\right) \\ P_n & f_n\left(x_1\right) & f_n\left(x_2\right) & f_n\left(x_j\right) & f_n\left(x_n\right) \end{array} P1P2PiPnP1f1(x1)f2(x1)fi(x1)fn(x1)P2f7(x2)f2(x2)fi(x2)fn(x2)Pjf7(xj)f2(xj)fi(xj)fn(xj)Pnf1(xn)f2(xn)fi(xn)fn(xn)(3) P j P_j Pj 收到其他参与者的值 s i j = f i ( x j ) , i = 1 , 2 , … , n s_{i j}=f_i\left(x_j\right), i=1,2, \ldots, n sij=fi(xj),i=1,2,…,n, 计算 s j = ∑ i = 1 n f i ( x j ) s_j=\sum_{i=1}^n f_i\left(x_j\right) sj=∑i=1nfi(xj) 作为 自己最终分享秘密的碎片。
从协议中可以看出, 若令 f ( x ) = ∑ i = 1 n f i ( x ) f(x)=\sum_{i=1}^n f_i(x) f(x)=∑i=1nfi(x), 则 f ( x j ) = ∑ i = 1 n f i ( x j ) f\left(x_j\right)=\sum_{i=1}^n f_i\left(x_j\right) f(xj)=∑i=1nfi(xj) 。
秘密重构阶段,只需任意 t t t个参与者使用自己拥有的秘密碎片 s i s_i si执行Shamir秘密分享体制的秘密重构即可。