目录

一、递归的定义

1、什么时候会用到递归的方法

1. 定义是递归的

2. 数据结构是递归的

3. 问题的解法是递归的 

2、应用递归的原则

3、递归调用顺序问题 

1. 首先递归的过程可以总结为以下几点：

2. 递归工作栈

二、 递归和非递归的转化

1. 单向递归可用迭代 

举例：斐波拉契数列

2. 尾递归可用迭代

举例：欧几里德求最大公约数

3. 借助栈实现非递归

1. 举例：二叉树的先序遍历

2. 举例：二叉树的中序遍历

三、分治解题步骤

四、汉诺塔问题

1. 问题

2. 解题思路 

3. 两个盘子演示

4. 三个盘子演示

5. 四个盘子演示 

6. 代码

---

一、递归的定义

在数学及程序设计方法学中为递归下的定义是这样的：若一个对象部分包含地包含它自己，或用它自己来定义它自己，则称这个对象是递归的；若一个过程直接或间接的调用自己，则称这个过程为递归的过程。简而言之，递归方法就是直接或间接地调用其自身

1、什么时候会用到递归的方法

1. 定义是递归的

以数学上常用的阶乘函数为例，其定义和计算都是递归的

定义：

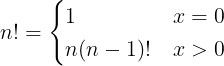
 求解函数：

int faction(int n){if (n == 1)return 1;elsen = faction(n - 1) * n;return n;}

2. 数据结构是递归的

链表就是一种递归的数据结构，从概念上讲，单链表可以递归的定义为一个结点，当该结点的指针域为NULL的时候，就表明此链表是一个单链表，这个结点的指针域也可以指向另一个单链表，而这个单链表具有同样的结构树也可以采用递归的方式来描述。首先一棵树要么是空，要么由若干非空子树组成（子树的数目可以为空），且这些子树的根都通过一条边连到根上。每个子树同样具有这样的结构，要么为空，要么由根和若干非空子树组成。

3. 问题的解法是递归的 

2、应用递归的原则

首先是必须要有一些“基本条件”能够采用非递归的方式计算得到，这是使用递归方法的重要前提。基本条件的满足意味着采用递归处理后的子问题可以直接解决时，就停止分解，而这些可以直接求解的问题就叫做递归的“基本条件”。为了使计算最终完结，任何递归调用都要朝着“基本条件”的方向进行。例1：前面所举例的阶乘

if (n == 1)   return 1;

 这就是所谓的基本条件。

例2：二分查找（折半查找） 

int BinSearch(int* data, int key,int low,int high)//折半查找{if (low > high)return -1;int mid = (low + high) / 2;//二分查找递归的核心部分if (key < data[mid])return(data, key, low, mid - 1);//继续在data[low,mid-1]左区间查找else if (key > data[mid])return(data, key, mid + 1, high);//继续在data[mid+1,high]右区间查找elsereturn mid;//查找成功}

其中：if(low>high)是基本条件之一，即在搜索范围内无法找到想要查找的值，表示搜索失败，递归过程也就结束了；此外，找到想要查找的值递归过程也会结束，也就是“return mid”，其对应的条件是“if(key==data[mid]”。

3、递归调用顺序问题 

1. 首先递归的过程可以总结为以下几点：

递归过程在实现时，需要自己调用自己层层向下递归，退出次序正好相反主程序第一次递归调用自己为内部调用它们返回调用它的过程的地址不同

2. 递归工作栈

在递归过程中，递归的执行需要一些薄记空间来记录跟踪前一个递归调用，特别对于那些有一长串递归调用的情况，在某种程度上较同等循环而言更加费时，因为薄记工作本身就要消耗一定时间。这个薄记空间就是递归工作栈。同时，每一次递归调用时，需要为过程中使用的参数、局部变量等另外分配存储空间。每层递归调用需分配函数递归时的活动记录 可以用如下图表示：

 

 以下列代码为例：

#include<iostream>using namespace std;void Fuction1(int n){if (n < 4){printf("%d\n", n);Fuction1(n + 1);}}void Fuction2(int n){if (n < 4){Fuction2(n + 1);printf("%d\n", n);}}int main(){cout << "第一个函数：" << endl;Fuction1(0);cout << "第二个函数：" << endl;Fuction2(0);return 0;}

Fuction1函数的执行过程

Fuction2函数执行过程：

二、 递归和非递归的转化

1. 单向递归可用迭代 

单向递归： 是指递归的过程总是朝着一个方向进行。斐波拉契数列的求解就是单向递归

举例：斐波拉契数列

递归求解斐波拉契数列： 

int Fib(int n){if (n < 2)return n == 0 ? 0 : 1;else if (n >= 2){n = Fib(n - 1) + Fib(n - 2);return n;}}

 迭代求解斐波拉契数列：

int Fib(int n){vector<int> v;v.push_back(0);v.push_back(1);int i = 2;for (i = 2; i <= n; i++){int t = v[i - 1] + v[i - 2];v.push_back(t);}return v[n];}

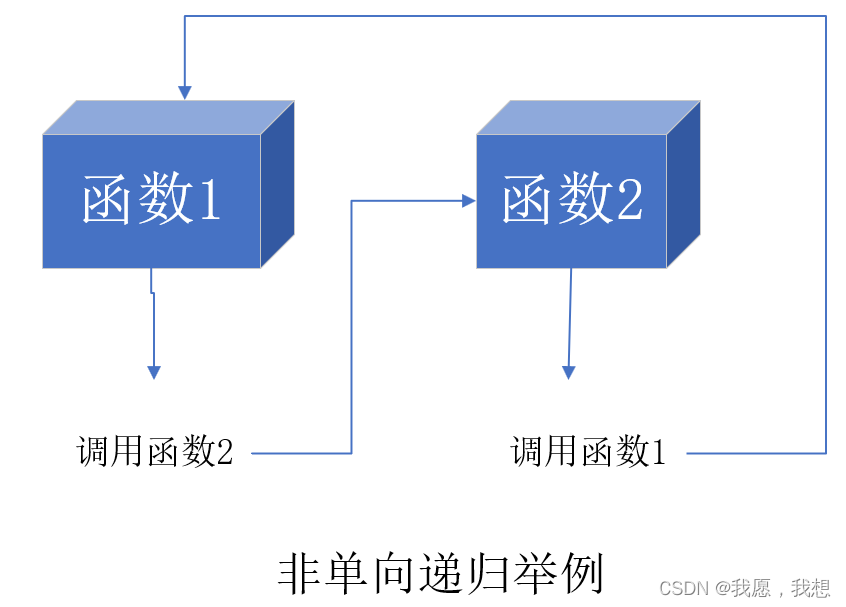
2. 尾递归可用迭代

尾递归函数是以递归调用作为结尾的函数，它是单向递归的特例，它的递归调用语句只有一个，而且放在过程最后。当递归调用返回时，返回到上一层递归调用语句的下一语句的时候，而这个位置正好是程序的结尾。尾递归示意图：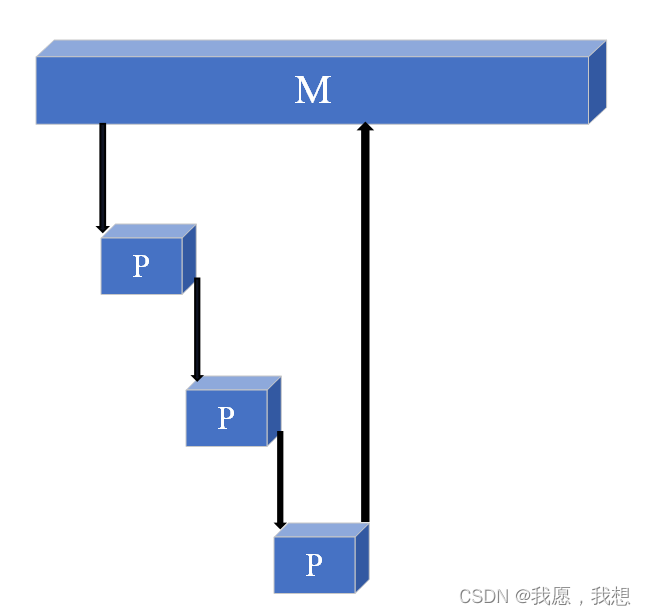

举例：欧几里德求最大公约数

是用较大的数除以较小的数，较小的除数和得出的余数构成新的一对数，继续做上面的除法，直到出现能够整除的两个数。 递归求解最大公约数：

int gcd(int a, int b){if (b == 0)return a;elsegcd(b, a % b);}

迭代求解最大公约数：

int gcd(int a, int b){int tmp;//保存a%bwhile (b!=0){tmp = a % b;a = b;b = tmp;}return a;}

3. 借助栈实现非递归

1. 举例：二叉树的先序遍历

递归先序遍历：

void PreOrder(BTree T)//先序遍历{    if (T != NULL)    {        cout << T->data << " ";//访问根结点        PreOrder(T->lchild);//先序遍历左子树        PreOrder(T->rchild);//先序遍历右子树    }}

用栈先序遍历：

bool First(BTree T){    stack<BTNode*>s;    BTNode* p = T;    if (p != NULL )//二叉树不为空    {        s.push(p);        while (!s.empty())//栈不为空        {            p = s.top();            cout << s.top()->data << " ";//先访问栈顶元素            s.pop();//栈顶元素退栈            if (p->lchild != NULL)                s.push(p->rchild);//栈顶元素的右孩子结点进栈            if (p->rchild != NULL)                s.push(p->lchild);//栈顶元素的左孩子结点进栈        }    }    return true;}

2. 举例：二叉树的中序遍历

递归中序遍历：

void InOrder(BTree T)//中序遍历{    if (T != NULL)    {        InOrder(T->lchild);        cout << T->data << " ";        InOrder(T->rchild);    }}

用栈中序遍历：

bool InOder(BTree T){    stack<BTNode*>s;    BTNode* p = T;    while (p != NULL || !s.empty())    {        while (p != NULL)//当前结点不为空        {            s.push(p);            p = p->lchild;        }        if (!s.empty())        {            cout << s.top()->data << " ";//访问栈顶元素            p = s.top()->rchild;//先将栈顶元素的右孩子存储起来            s.pop();//栈顶元素出栈        }    }    return true;}

三、分治解题步骤

1. 分解：将要解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题

2. 治理：求解各个子问题。由于各个子问题与原问题形式相同，只是规模较小而已，而当子问题划分得足够小时，就可以用较简单的方法解决

3. 合并：按原问题的要求，将子问题的解逐层合并构成原问题的解 

 解决方案示意图：

四、汉诺塔问题

1. 问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制：每次只能移动一个盘子;盘子只能从柱子顶端滑出移到下一根柱子;盘子只能叠在比它大的盘子上。将所有盘子从第一根柱子移到最后一根柱子 

2. 解题思路 

当n=1（盘子数目为1）的时候，只需将盘子从A移到C即可当n>1（盘子数目大于1）的时候，利用B作为辅助，将n-1个较小的盘子从A移到B，再将剩余的一个盘子从A移动到C。最后再将n-1个小盘从B依次移动到C。

3. 两个盘子演示

4. 三个盘子演示

5. 四个盘子演示 

6. 代码

#include<iostream>using namespace std;void Move(int n, char x, char y){cout << "将编号为" << n << "的盘子从" << x << "移向" << y << endl;}void hanota(int n,char a,char b,char c){if (n == 1)Move(1, a, c);else{hanota(n - 1, a, c, b);//将n-1个盘子从a移到bMove(n, a, c);//将剩下的第n个盘子直接移到c处hanota(n - 1, b, a, c);//又将n-1个盘子从b移到c}}int main(){hanota(3, 'A', 'B', 'C');return 0;}