????
欢迎来到茶色岛独家岛屿,本期将为大家揭晓LeetCode 96. 不同的二叉搜索树,做好准备了么,那么开始吧。
????
一、题目名称
二、题目要求
三、相应举例
四、限制要求
五、解决办法
六、代码实现
方法一:动态规划
方法二:递归
一、题目名称
LeetCode 96. 不同的二叉搜索树
二、题目要求
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
三、相应举例
示例 1:
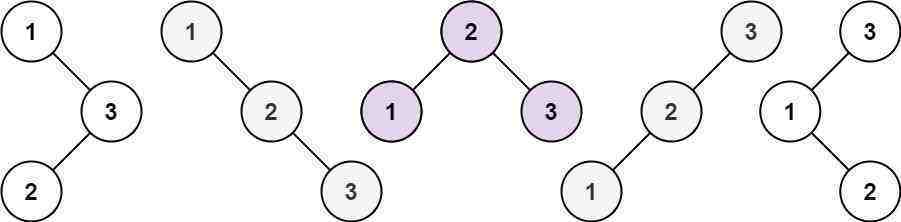
输入:n = 3输出:5
示例 2:
输入:n = 1输出:1
四、限制要求
1 <= n <= 8五、解决办法
动态规划
题目要求是计算不同二叉搜索树的个数。为此,我们可以定义两个函数:
G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。
F(i, n): 以 i为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。
可见,G(n) 是我们求解需要的函数。
稍后我们将看到,G(n) 可以从 F(i,n) 得到,而F(i,n) 又会递归地依赖于 G(n)。
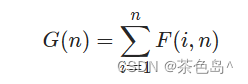
对于边界情况,当序列长度为 1(只有根)或为 0(空树)时,只有一种情况,即:
G(0)=1,G(1)=1
六、代码实现
方法一:动态规划
class Solution { public int numTrees(int n) { int[] G = new int[n + 1]; G[0] = 1; G[1] = 1; for (int i = 2; i <= n; ++i) { for (int j = 1; j <= i; ++j) { G[i] += G[j - 1] * G[i - j]; } } return G[n]; }}外层for循环是遍历G中从2开始到n的每个节点,目的是为了求出类似于G(2),G(3)等等,若直接使用下面的循环,如下图:

刚开始会出现G(2)=0,求出G(n)=0的现象,而
使用外层循环可以依次求出G(2),G(3)等,即节点的二叉搜索树的种数,可以防止这种情况出现。如下图:

每次循环可依次求出G(2),G(3)等二叉搜索树的种数,直到最后求G(n)。
方法二:递归
Map<Integer, Integer> map = new HashMap<>(); public int numTrees(int n) { if (n == 0 || n == 1){ return 1; } //防止重复递归查找 if (map.containsKey(n)){ return map.get(n); } int count = 0; //当i为根节点时 for (int i = 1; i <= n; i++) { count+=numTrees(i-1)*numTrees(n-i); } map.put(n,count); return count; }
