 猛戳!跟哥们一起玩蛇啊 ? 《一起玩蛇》?
猛戳!跟哥们一起玩蛇啊 ? 《一起玩蛇》?
? 写在前面:这个系列似乎反响不错, 所以我继续水下去 (bushi)。本篇博客是关于经典的 Cross Product and Convex Hull (向量叉积和凸包)的,我们将介绍引射线法,葛立恒扫描法。在讲解之前我会对前置知识做一个简单的介绍,比如向量叉积,如何确定直线是在顺时针上还是逆时针上等。算法讲解部分是为后面练习题做准备的,比如如何判断内点是否在多边形内,如何计算多边形面积等,还将简单介绍一下葛立恒扫描法,在提供的练习题中就能碰到。练习代码量200行左右,如果感兴趣想尝试做的话,需要有一定的耐心。练习题的环境为 Google Colaboratory(K80 GPU)Jupyter Notebook:colab
Ⅰ. 前置知识
0x00 向量叉积(Cross product)
? 概念:向量积 (Cross product),也可以称之为 "向量叉积" 。我更愿意称之为 "向量叉积",因为可以顾名思义 —— 叉积,交叉乘积!
" 叉积,叉积……积……?! 积你太美!"
 咳咳…… 它是一种在向量空间中向量的二元运算。
咳咳…… 它是一种在向量空间中向量的二元运算。
向量叉积不同于点积!其运算结果是一个向量,而非标量。
并且两个向量的叉积与这两个向量垂直。表示方法为 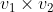 ,期中
,期中  代表向量。
代表向量。
? 定义如下:
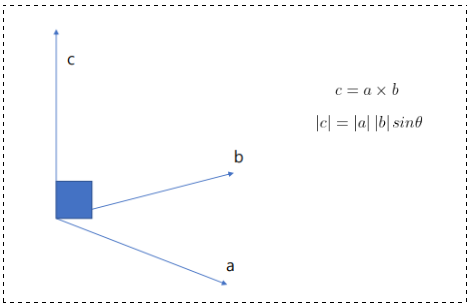
模长:这里的 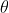 表示两向量之间的夹角(共起点的前提下),范围
表示两向量之间的夹角(共起点的前提下),范围 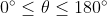 ,它位于这两个矢量所定义的平面上。
,它位于这两个矢量所定义的平面上。
方向:a向量与b向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。
 的长度在数值上等于以
的长度在数值上等于以 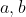 ,夹角为
,夹角为 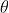 组成的平行四边形面积。因为在不同的坐标系中
组成的平行四边形面积。因为在不同的坐标系中  可能不同,所以运算结果
可能不同,所以运算结果  是一个伪向量。
是一个伪向量。
两向量的三角形的面积:
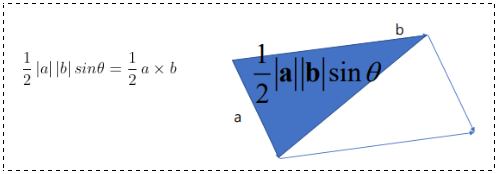
令向量  和
和 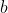 都在平面
都在平面 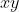 上:
上:

0x01 确定顺时针逆时针(Clockwise or Counter-clockwise)

❓ 有什么好办法,可以确定点在直线  是在顺时针上还是逆时针上?
是在顺时针上还是逆时针上?
 我们可以用 叉积 "暗中观察" 点是否在直线
我们可以用 叉积 "暗中观察" 点是否在直线 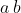 的顺时针或逆时针方向上:
的顺时针或逆时针方向上:
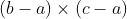 的叉积指向显示的前方,∴
的叉积指向显示的前方,∴ 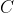 点在逆时针方向。∵
点在逆时针方向。∵ 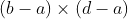 的叉积指向显示的后方,∴
的叉积指向显示的后方,∴ 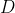 点在顺时针方向。
点在顺时针方向。
0x02 交叉点(Intersection)
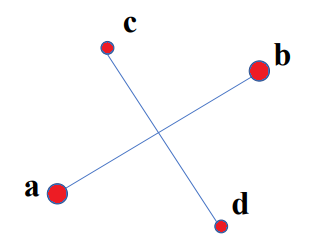
 当每条线的端点位于另一条线的不同侧面时,两条线就会交叉:
当每条线的端点位于另一条线的不同侧面时,两条线就会交叉:
Ⅱ. 算法讲解部分
0x00 判断内点是否在多边形内(Inner points)
❓ 思考:如何检查平面上的一个点(point)是否在多边形内部?

这里我介绍两种常用的方法,只在一侧法 和 引射线法。
① "只在一侧" 法:
只在一侧 (only on the one side) ,当一个点在每个多边形边的一侧(顺时针或逆时针)时,该点就在多边形的内部。

② 引射线法:
从目标点出发引一条射线,观察这条射线和多边形所有边的交点数目。如果有奇数个交点,则说明在内部,如果有偶数个交点,则说明在外部。

图中的红点是需要测试的点(我已标出),我们要确定它是否位于多边形内。
? 解决方案:将多边形的每一边与测试点的 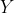 (垂直)坐标进行比较,并编译一个结点列表,其中每个节点是一个边与测试点的
(垂直)坐标进行比较,并编译一个结点列表,其中每个节点是一个边与测试点的 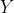 阈值相交的点。在此示例中的多边形的 8 条边越过
阈值相交的点。在此示例中的多边形的 8 条边越过 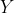 阈值,而其他 6 条边则没有。那么,如果有奇数测试点每边的节点数,那就说明它在多边形内。如果测试点的每一侧都有偶数个节点,那么它在多边形之外。
阈值,而其他 6 条边则没有。那么,如果有奇数测试点每边的节点数,那就说明它在多边形内。如果测试点的每一侧都有偶数个节点,那么它在多边形之外。
在本示例中,测试点左侧有5个节点,右侧有3个节点。由于 5 和 3 是奇数,该测试点在多边形内。(注意:该算法不关心多边形是顺时针还是逆时针跟踪)
0x01 计算多边形的面积
? 思路:
按逆时针方向对顶点进行排序。找到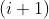 个顶点位于第
个顶点位于第 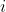 个节点和第
个节点和第 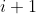 个节点的边缘的顺时针方向的三角形,并积累三角形的面积。删除三角形并再次重复该过程,直到没有顶点为止。
个节点的边缘的顺时针方向的三角形,并积累三角形的面积。删除三角形并再次重复该过程,直到没有顶点为止。
将所有边缘的叉积加起来,然后除以2。
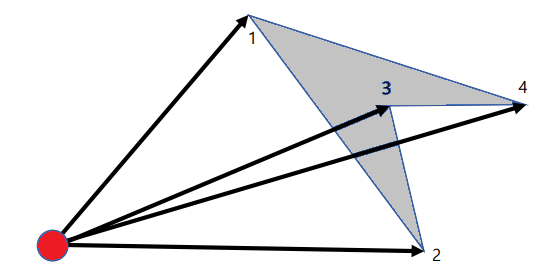
sum += float(x1 * y2 - x2 * y1);根据一条边的方向,添加或减去三角形的面积。
 令人惊讶的是,只留下了多边形的面积:
令人惊讶的是,只留下了多边形的面积:
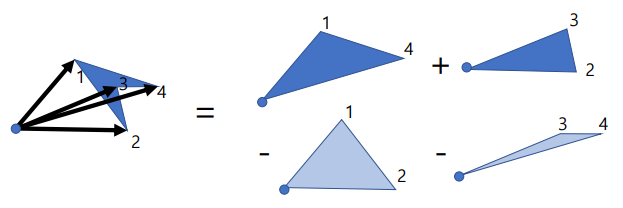
? 提示:其类似于边的叉积之和

0x02 葛立恒扫描法(Graham Scan)
凸包计算(Computing a convex hull),给定平面点:

葛立恒扫描法(Graham Scan)
葛立恒扫描法(Graham's scan)是一种计算一组的平面点的凸包的算法。以在1972年发表该算法的葛立恒命名。


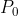 (一定在凸包上)。以
(一定在凸包上)。以 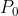 为原点,将其他的点按照极坐标排序,角度小的排在前,若角度相同,距离近的排在前。
为原点,将其他的点按照极坐标排序,角度小的排在前,若角度相同,距离近的排在前。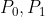 入栈,从
入栈,从 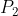 (第三个点)开始,若
(第三个点)开始,若 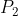 在直线
在直线 ![P_0 P_1(\, p\, [ i-1 ] \, p [ i ]\, )](http://zhangshiyu.com/zb_users/upload/2023/01/20230112141018167350381840164.gif) 的左边 ,则
的左边 ,则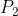 入栈,否则
入栈,否则 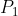 出栈,一直遍历完后面所有点 (这里就需要向量叉乘来判断点在线的左边还是右边)。最后留在栈中的点就是凸包上的点。
出栈,一直遍历完后面所有点 (这里就需要向量叉乘来判断点在线的左边还是右边)。最后留在栈中的点就是凸包上的点。
Ⅲ. 练习(Assignment)
? 注意:需用 Python 实现,算法必须在不导入外部库的情况下实现,但允许使用 numpy、math、sort 相关函数。(如果不加以限制,直接导某包掉函数就能直接算凸包,那还练个锤子,知道的小伙伴可以在评论区扣出来)
环境推荐:Colab
任务1:计算多边形面积
给定由 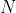 个点构成的平面多边形 ,计算该多边形的面积。
个点构成的平面多边形 ,计算该多边形的面积。
| input | Output |
| 5 0 0 2 0 2 2 1 1 0 2 | 3 |
任务2:多边形坐标
给定的  个构成多边形的点和
个构成多边形的点和 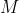 个检查点,判断每个检查点是否在多边形内。
个检查点,判断每个检查点是否在多边形内。
* 注:在边缘线上的点也视作在多边形内。
| input | Output |
| 5 // N points 0 0 // (x1, y1) 2 0 // (x2, y2) 2 2 1 1 0 2 2 0 0 0.5 0.5 -1 -1 | Inside Inside Outside |
读取 input1.txt , input2, input3.txt,将结果分别生成到 output1.txt , _output3.txt 。
这里的 txt 文件请复制粘贴下面的数据,请自行创建!
? input1.txt
80 2724 8766 7138 3173 838 4979 89? input2.txt
61 8014 1068 1124 2120 3195 901 6014 5479 4720 1459 2291 1318 9851 9223 3059 5382 8465 2879 341 2167 8229 613 533 5881 590 6749 4774 355 794 7650 3685 087 6633 7878 6485 1113 1761 4717 921 9930 95100 1864 9368 7146 7659 6131 5627 5237 4885 9738 8825 8019 3826 652 8625 3068 4352 1297 7934 63? input3.txt
46 4415 5459 685 5059 9877 9232 8899 1234 370 8388 6183 6937 124 9021 10028 9567 4418 3379 5980 8894 9422 3089 309 8368 7745 9556 10028 531 5214 4980 8195 5796 2880 2787 2942 520 919 7265 788 2640 256 3068 1954 5855 5313 4630 1432 4550 6885 2344 10012 9914 645 939 4955 244 9329 359 290 8538 4533 1367 8959 516 9415 4875 727 5851 4959 51输出文件命名为 output1, output2, output3,输出结果演示:

生成 output 文件后,每个 output 都要画出图像,这里就不需要大家自己画了,
提供了 display.py,这是用于生成图像的代码。
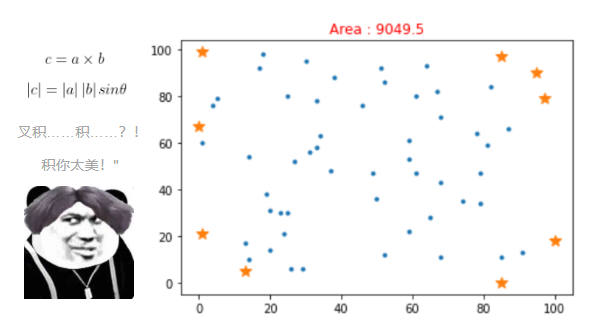
def display(input_txt_path, output_txt_path): import matplotlib.pyplot as plt ''' input1:input_txt_path=input_example.txt的路径 input2:output_txt_path=output_example.txt的路径 return:保存conex_hull图像 ''' with open(input_txt_path, "r") as f: input_lines = f.readlines() with open(output_txt_path, "r") as f: output_lines = f.readlines() whole_points = input_lines area = round(float(output_lines[0]), 1) hull_points = output_lines[1:] x_list = [int(x.split(" ")[0]) for x in whole_points] y_list = [int(x.split(" ")[1]) for x in whole_points] plt.plot(x_list, y_list, marker='.', linestyle='None') hx_list = [int(x.split(" ")[0]) for x in hull_points] hy_list = [int(x.split(" ")[1]) for x in hull_points] plt.plot(hx_list, hy_list, marker='*', linestyle='None', markersize=10) title = plt.title(f'Area : {area}') plt.setp(title, color='r') plt.savefig(output_txt_path[:-3]+"png", bbox_inches='tight')if __name__ == "__main__": input_txt_path = "./input_example.txt" output_txt_path = "./output_example.txt" display(input_txt_path, output_txt_path)通过调用提供的 display 函数,生成的图像效果如下:

任务3:点是否在多边形内
给定 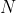 个点构成平面多边形,计算凸包及其面积。
个点构成平面多边形,计算凸包及其面积。
| input | Output |
| 5 // N 个点 0 0 // (x1, y1) 2 0 // (x2, y2) 2 2 1 1 0 2 | 4 (0, 0), (2, 0), (2, 2), and (0, 2) are points of convex hull. |
您可以从 point_in_polygon_input.txt 输入 5 个坐标,并将它们与在刚才实现的 "练习1" 中保存的output1, output2, output3.txt 的多边形进行比较,以 "in" 或 "out" 的形式输入5个坐标。
这里的 point_in_polygon_input.txt 仍然是要自己创建,复制粘贴手动创建:
point_in_ploygon_input.txt:
0 01 110 1050 5070 70因此,与3个 output1-3.txt 的文件相比,必须生成 3 个output 文件,格式演示如下:
参考代码
# -*- coding: utf-8 -*-import mathdef read_points(p): L = [] with open(p, 'r') as FILE: line = FILE.readlines() Lx, Ly = [int(i.split(" ")[0]) for i in line], [int(i.split(" ")[1]) for i in line] cur, sz = 0, len(Lx) for cur in range(sz): x, y = Lx[cur], Ly[cur] L.append( (x, y) ) return Ldef get_rad(px, py): pi = math.pi a = px[0] - py[0] b = px[1] - py[1] if a == 0: if b: return pi / 2 else: return -1 rad = math.atan(float(b) / float(a)) if rad < 0: return rad + pi else: return raddef sort_points_tan(p, pk): L = [] resL = [] i = 0 sz = len(p) for i in range(sz): L.append({"index": i, "rad": get_rad(p[i], pk)}) L.sort(key=lambda k: (k.get('rad'))) sz = len(L) for i in range(sz): resL.append(p[L[i]["index"]]) return resLdef calc_area(points): sz = len(points) points.append(points[0]) S = 0 for i in range(sz): S += (points[i][0] + points[i + 1][0]) * (points[i + 1][1] - points[i][1]) return abs(S) / 2def convex_hull(p): p = list(set(p)) k = 0 sz = len(p) for i in range(1, sz): if p[i][1] < p[k][1]: k = i if (p[i][0] < p[k][0]) and (p[i][1] == p[k][1]): k = i pk = p[k] p.remove(p[k]) p_sort = sort_points_tan(p, pk) L = [pk, p_sort[0]] sz = len(p_sort) for i in range(1, sz): while (( (L[-2][0] - L[-1][0]) * (p_sort[i][1] - L[-1][1]) - (p_sort[i][0] - L[-1][0]) * (L[-2][1] - L[-1][1]) ) > 0): L.pop() L.append(p_sort[i]) return Ldef check(sp, ep, p): if sp[0] < p[0] and ep[1] > p[1]: return False if sp[1] == p[1] and ep[1] > p[1]: return False if ep[1] == p[1] and sp[1] > p[1]: return False if sp[1] == ep[1]: return False if sp[1] > p[1] and ep[1] > p[1]: return False if sp[1] < p[1] and ep[1] < p[1]: return False if ep[0] - (ep[0] - sp[0]) * (ep[1] - p[1]) / (ep[1] - sp[1]) < p[0]: return False return Truedef inpoly(p, poly_points): cnt = 0 i = 0 sz = len(poly_points) for i in range(sz): p1, p2 = poly_points[i], poly_points[(i + 1) % sz] if check(p1, p2, p): cnt += 1 if cnt % 2 == 1: return True else: return Falsedef write_in_out(test_points, poly_points, out_txt_path): with open(out_txt_path, "w") as FILE: i = 0 for i in test_points: if inpoly(i, poly_points): FILE.write("in") else: FILE.write("out") FILE.write("\n")def write_area(poly_points,out_path): res = convex_hull(poly_points) with open(out_path,"w") as FILE: FILE.write(str(calc_area(res))) FILE.write('\n') sz = len(res) for i in range(sz - 1) : FILE.write(str( res[i][0])) FILE.write(" ") FILE.write(str(res[i][1])) FILE.write("\n") return restest_points = read_points("point_in_polygon_input.txt")poly_out_path = "foxny_point_in_polygon_output1.txt" #####poly_points = read_points("input1.txt") ####area = write_area(poly_points, "foxny_output1.txt") ######write_in_out(test_points , area, poly_out_path)def display(input_txt_path, output_txt_path): import matplotlib.pyplot as plt ''' input1 : input_txt_path = path of input_example.txt input2 : output_txt_path = path of output_example.txt return : save convex_hull image ''' with open(input_txt_path, "r") as f: input_lines = f.readlines() with open(output_txt_path, "r") as f: output_lines = f.readlines() whole_points = input_lines area = round(float(output_lines[0]), 1) hull_points = output_lines[1:] x_list = [int(x.split(" ")[0]) for x in whole_points] y_list = [int(x.split(" ")[1]) for x in whole_points] plt.plot(x_list, y_list, marker='.', linestyle='None') hx_list = [int(x.split(" ")[0]) for x in hull_points] hy_list = [int(x.split(" ")[1]) for x in hull_points] plt.plot(hx_list, hy_list, marker='*', linestyle='None', markersize=10) title = plt.title(f'Area : {area}') plt.setp(title, color='r') plt.savefig(output_txt_path[:-3]+"png", bbox_inches='tight')####################################################################################1if __name__ == "__main__": input_txt_path = "input1.txt" output_txt_path = "foxny_output1.txt" display(input_txt_path, output_txt_path)""? 结果演示:
foxny_output1.png

foxny_ouput2.txt
3568.080 2779 8924 878 4938 31foxny_output2.png
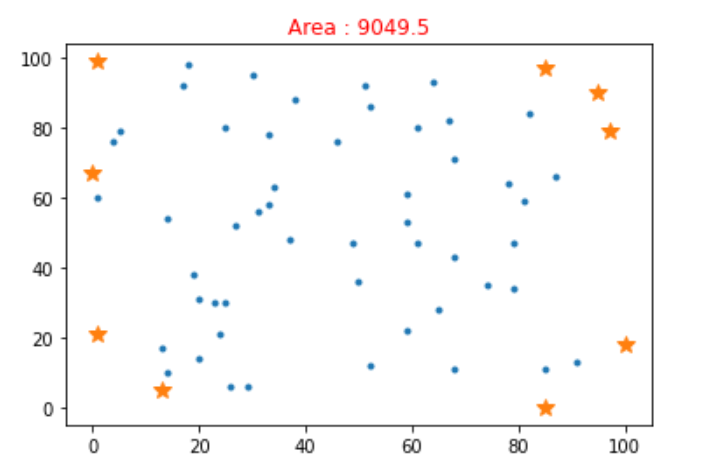
foxny_output2.txt
9049.585 0100 1897 7995 9085 971 990 671 2113 5foxny_output3.png
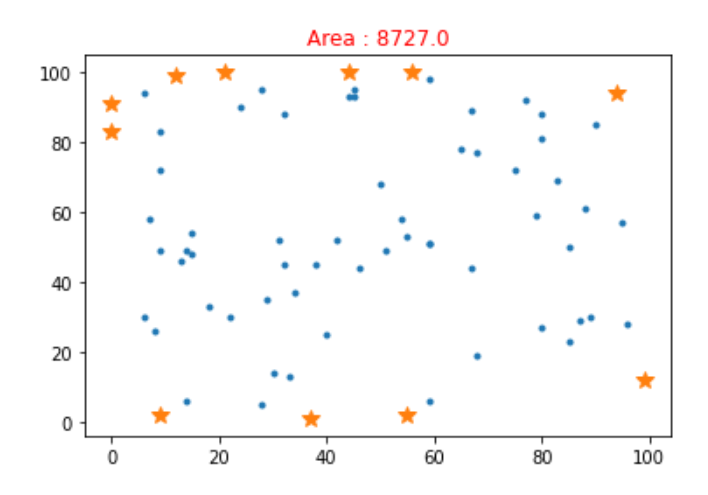
foxny_output3.txt
8727.037 155 299 1294 9456 10021 10012 990 910 839 2foxny_point_in_polygon_output1.txt
outoutoutininfoxny_point_in_polygon_output2.txt
outoutinininfoxny_point_in_polygon_output3.txt
outoutininin

? [ 笔者 ] 王亦优? [ 更新 ] 2022.12.12❌ [ 勘误 ] /* 暂无 */? [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免, 本人也很想知道这些错误,恳望读者批评指正!| ? 参考资料 Darel Rex Finley. Point-In-Polygon Algorithm — Determining Whether A Point Is Inside A Complex Polygon[EB/OL]. 1998,2006,2007[2022.12.12]. http://alienryderflex.com/polygon/. C++reference[EB/OL]. []. http://www.cplusplus.com/reference/. Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/. |