高斯滤波器讲解(python实现)
文章目录
1.高斯滤波器2.高斯函数讲解(1)高斯函数(2)参数详解(3)高斯函数具体实现过程(3)那这里的sigmaX,sigmaY,ksize是怎么实现卷积并且对图像进行滤波的呢?(1)为什么要使用sigmaX和sigmaY呢?(2)卷积核(权重矩阵)中的值具体计算 3.代码实战(1)当sigma=0.0时,随着ksize的不同,平滑的效果(2)当设置sigma的值不为0的时候,随着sigma增加对图像的平滑效果
1.高斯滤波器
比均值滤波处理图像更加的平滑,边界保留效果更加好;
高斯滤波是一种线性滤波器,能够有效的抑制噪声,平滑图像。其作用原理和均值滤波器类似,都是取滤波器窗口内的像素的均值作为输出。但其窗口模板的系数和均值滤波器不同,均值滤波器的模板系数都是相同的为1,而高斯滤波器的模板系数则随着距离模板中心的增大而减小。所以,高斯滤波器相比于均值滤波器对图像个模糊程度较小.
比如下面的一块图像区域的像素值与权值矩阵的乘积(权值矩阵代表卷积核):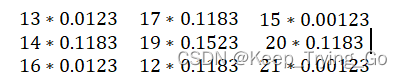
可以看到这个核,距离中心的19越远的系数所占的比重越少,那么对图像的模糊程度也越小。
注:如果噪声的概率密度函数服从高斯分布的就叫做高斯噪声。
关于方盒滤波和均值滤波:
https://mydreamambitious.blog.csdn.net/article/details/125173270
2.高斯函数讲解
(这里将高斯函数和高斯函数的具体应用过程一起讲)
(1)高斯函数
GaussianBlur(src, ksize, sigmaX, dst=None, sigmaY=None, borderType=None);
(2)参数详解
(1)src:表示输入的原图像;(2)Ksize:表示卷积核(高斯核)大小(ksize(w,h),w-像素宽度,h-像素高度);(3)sigmaX:X方向的滤波核;表示卷积核在X方向上的标准差,控制的是权重比例;(4)sigmaY:Y方向的滤波核;表示卷积核在Y方向上的标准差,控制的是权重比例;
如果 sigmaY 为零,则将其设置为等于 sigmaX;如果两个sigma均为零,则分别根据ksize.width 和 进行计算 ksize.height完全控制的结果,无论这一切的语义未来可能的修改,建议指定所有的ksize,sigmaX和sigmaY。
sigmaX = 0.3 x ((ksize.width-1) x 0.5 - 1) + 0.8
sigmaY = 0.3 x ((ksize.height-1) x 0.5 - 1) + 0.8
(5)borderType:推断图像外部像素的某种边界模式。有默认值BORDER_DEFAULT.
(3)高斯函数具体实现过程
基于二维高斯函数,构建权重矩阵,进而构建高斯核,最终对每个像素点进行滤波处理(平滑、去噪)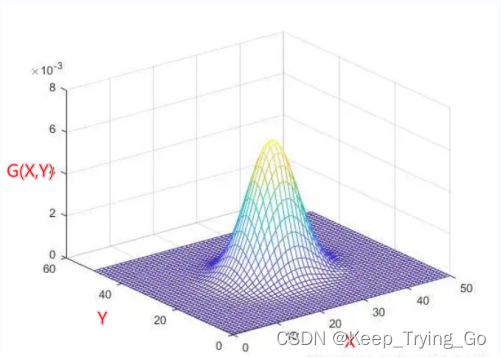
思考:1.为什么可以通过设置高斯函数的sigma值对图像进行平滑操作呢?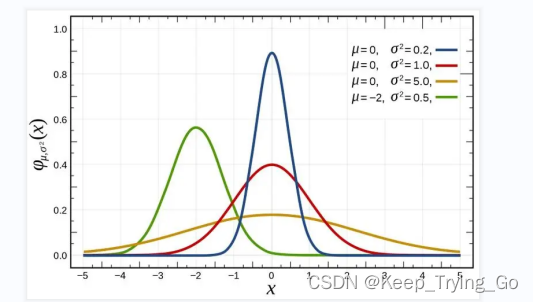
解释:其实大家也知道,当μ=0的时候,图像关于Y轴对称,当σ的值不断变化时,图像的“高瘦”也不断变化,当σ的值变大时,图像越分散(“矮”);相反这越高;通过这样的变化,可以想到我们图像的像素周围的值和高斯函数这样图像的变换的关系。通过这样的方式对图像进行模糊(可能这里还是没有解释清楚)
(3)那这里的sigmaX,sigmaY,ksize是怎么实现卷积并且对图像进行滤波的呢?
(1)为什么要使用sigmaX和sigmaY呢?
解释:因为高斯滤波是一种线性滤波器,为了处理二维的图像,所以使用sigmaX和sigmaY分别对水平和竖直方向进行操作。但是在opencv中首先是使用如下函数得到“水平”放向上的卷积核;然后再调用该函数得到“竖直”放向上的卷积核。(但是其实opencv中并没有具体实现直接使用二维的卷积核,而是通过两个一维的卷积实现的)
具体实现过程如下:
Mat getGaussianKernel( int ksize, //一维垂直方向上高斯核的行数 double sigma, //标准差 int ktype = CV_64F //返回值的数据类型 )得到两个卷积核之后使用opencv中的sepFilter2D函数进行行和列的卷积:最终结果按增量移位后存储在dst中。(下图就是sigmaX和sigmaY通过函数getGaussianKernel产生的两个卷积核,分别是水平和竖直的对图像的一部分区域进行卷积,最后得到一个像素值,这个是像素值就是卷积之后的结果)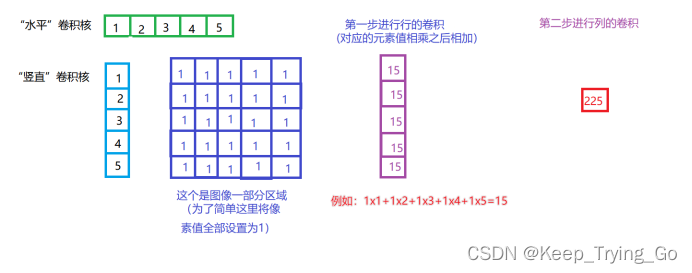
(2)卷积核(权重矩阵)中的值具体计算
首先看一下二维的高斯公式:这里的X,Y随机变量相互独立。
关于X的一维高斯函数(正态分布):
由于高斯滤波器是以模板的中心位置为坐标原点进行取样,以3x3大小的矩阵为例: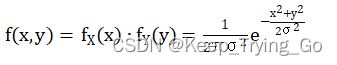
通过这个公式计算卷积核(权重矩阵):
其中的sigma是我们给出的,那么x,y是怎么得到呢?(看下图)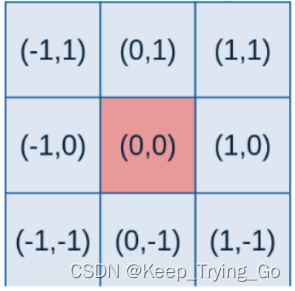
这个矩阵周围的点通过
左上点: (x-1,y+1)
顶点: (x,y+1)
右上点:(x+1,y+1)
右边顶点:(x+1,y)
左边顶点(x-1,y)
左下角顶点:(x-1,y-1)
底部顶点:(x,y-1)
右下角顶点:(x+1,y-1)
这个方式计算,通过上面的这个矩阵可以算出卷积核的值(权重值矩阵,如下计算结果)
注:以公式计算出的中心数据值是最大的,也就是在对图像进行卷积的时候,中心像素值所占比例最大,随着离中心距离越大,权重所占比例越小,可这说明了什么?因为我们计算要对图像进行平滑(通过模糊的方式),那么一个像素点周围的像素值很大程度是有关系的,随着离这个像素中心点的距离越远,像素之间的关系越远,上面我们谈到过,一维高斯图像随着σ变化和我们平滑图像是什么关系,其实是通过高斯公式计算出权重矩阵,而这个权重矩阵也满足随着离像素中心点的距离越远,像素值之间的关系越小。所以随着σ的变大,权重矩阵的各个权重值相差就不是很大,比较类似均值模版,对图像的平滑效果比较明显。
总结:所以以后在设置sigmaX和sigmaY的时候可以更清楚其工作的具体过程,sigma设置的越大,同样的3x3矩阵计算出的权值相差不是很大,接近于均值滤波,对图像平滑处理效果更加明显(下面用代码实例演示效果)。
3.代码实战
import osimport cv2import randomimport numpy as npdef GaussFilter(img_path='images/lenna_GaussNoise.png'): img_src=cv2.imread(img_path) img=cv2.resize(src=img_src,dsize=(450,450)) img=cv2.GaussianBlur(src=img,ksize=(5,5),sigmaX=0,sigmaY=1.0) cv2.imshow('img',img) cv2.imshow('img_src',img_src) cv2.waitKey(0) cv2.destroyAllWindows()if __name__ == '__main__': print('Pycharm') GaussFilter()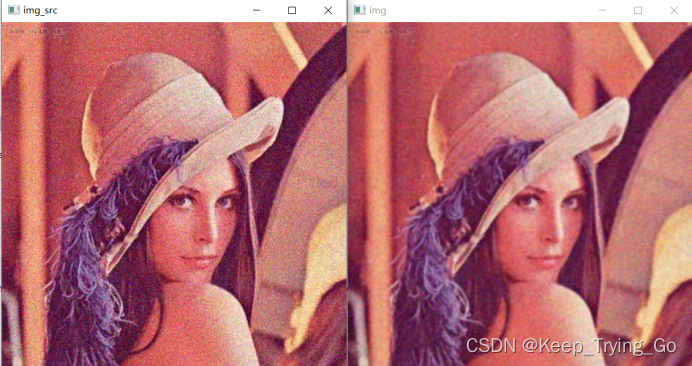
(1)当sigma=0.0时,随着ksize的不同,平滑的效果
#无sigma的处理def GaussFilter(img_path='images/lenna_GaussNoise.png'): img_src=cv2.imread(img_path) img=cv2.resize(src=img_src,dsize=(450,450)) img_5x5=cv2.GaussianBlur(src=img,ksize=(5,5),sigmaX=0) img_11x11 = cv2.GaussianBlur(src=img, ksize=(11,11), sigmaX=0) img_27x27 = cv2.GaussianBlur(src=img, ksize=(27,27), sigmaX=0) cv2.imshow('img_src', img_src) cv2.imshow('img_5x5',img_5x5) cv2.imshow('img_10x10', img_11x11) cv2.imshow('img_20x20', img_27x27) cv2.waitKey(0) cv2.destroyAllWindows()
(2)当设置sigma的值不为0的时候,随着sigma增加对图像的平滑效果
def GaussFilterSigmax(img_path='images/lenna_GaussNoise.png'): img_src=cv2.imread(img_path) img=cv2.resize(src=img_src,dsize=(450,450)) img_sigma_1=cv2.GaussianBlur(src=img,ksize=(5,5),sigmaX=1.0) img_sigma_5 = cv2.GaussianBlur(src=img, ksize=(11,11), sigmaX=5.0) img_sigma_10 = cv2.GaussianBlur(src=img, ksize=(27, 27), sigmaX=10.0) cv2.imshow('img_src', img_src) cv2.imshow('img_sigma_1',img_sigma_1) cv2.imshow('img_sigma_5', img_sigma_5) cv2.imshow('img_sigma_10', img_sigma_10) cv2.waitKey(0) cv2.destroyAllWindows()
可以看到随着sigma的增加,对图像的平滑处理更加的明显。
https://blog.csdn.net/jiangyutongyangyi/article/details/105281262
https://blog.csdn.net/jgj123321/article/details/94448463

登录后可发表评论
点击登录