Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
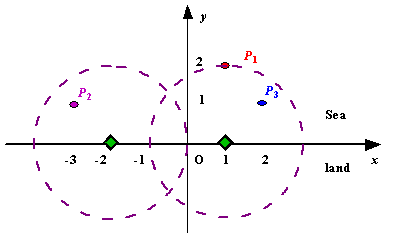
Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 21 2-3 12 11 20 20 0
Sample Output
Case 1: 2Case 2: 1
Source
#include<cstdio>#include<set>#include<map>#include<cstring>#include<algorithm>#include<queue>#include<iostream>#include<string>#include<cmath>using namespace std;typedef long long LL;#define MAXN 1003/*对于每个点可以在坐标轴上 得出能覆盖到该点的圆心范围,从而转化为x轴上的很多线段选取一定数目的点,让所有的线段都包含至少一个点先按结尾端点排序,然后尽量将雷达分布在右端(这样能尽可能和多个线段重叠)*/struct node{ double beg,end;}a[MAXN];int n,d;void cal(double x,double y,double &beg,double &end)//要求y<=d{ double r = (double)d; beg = x - sqrt(r*r-y*y); end = x + sqrt(r*r-y*y);}bool cmp(node a,node b){ return a.end<b.end;}int main(){ int cas = 1; while(scanf("%d%d",&n,&d),n+d) { double x,y; bool f = false; for(int i=0;i<n;i++) { scanf("%lf%lf",&x,&y); if(!f&&y<=d) cal(x,y,a[i].beg,a[i].end); else { f = true; } } if(f) { printf("Case %d: -1\n",cas++); continue; } sort(a,a+n,cmp); int cnt = 1; double tmp = a[0].end; for(int i=1;i<n;i++) { if(a[i].beg<=tmp)//因为是按结尾排序的, //所以a[i].end肯定大于等于tmp,这种情况说明无需添加新的雷达 continue; else//新的端点 起点无法包含,那么重新设置一个雷达(设置在新的线段最右端) { cnt++; tmp = a[i].end; } } printf("Case %d: %d\n",cas++,cnt); } return 0;}