这篇笔记记录求大数据topk的两种方法,分别是大小二叉堆法和快速分割法,下面依次详解这两种方法的过程。
1 大/小根堆法
利用大根堆过滤前top k小的数据**;小根堆过滤前top k大的数据**;
下面用大根堆求前k个小元素为例。
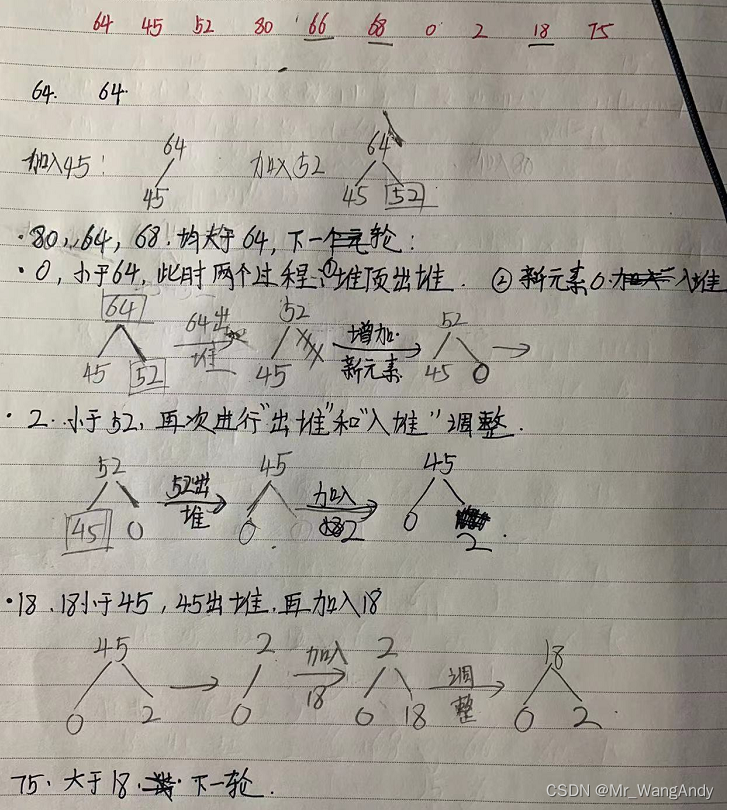
把大根堆堆顶的大值不断的淘汰,放入小值。先构建k个元素的大小堆(比如k=3,就是求数列中前3个元素),然后用数列中的元素依次与堆顶元素比较,如果大于或者小于堆顶元素,就进行出堆调整;最后再进行入堆调整。过程
先用数列中前k个元素构建一个堆,比如构建一个大根堆。新元素与堆顶元素比较,大于堆顶元素就进行下一个元素;如果新元素比堆顶元素小,堆顶元素先出堆,然后将新元素加入到堆中。
代码
#include <iostream>#include <vector>#include <time.h>#include <queue>#include <functional>using namespace std;int main(){vector<int> vec;srand(time(NULL));for (int i = 0; i < 10; i++){vec.push_back(rand() % 100);cout << vec[i] << " ";}cout << endl;// 求vec中值最小的前5个元素priority_queue<int> maxheap;int k = 5;// 前5个元素入堆for (int i = 0; i < 5; i++){maxheap.push(vec[i]);}// 遍历剩余元素,直到最后for (int i = 5; i < vec.size(); i++){if (maxheap.top() > vec[i]){maxheap.pop();maxheap.push(vec[i]);}}// 输出结果 while (!maxheap.empty()){cout << maxheap.top() << " ";maxheap.pop();}cout << endl;求出序列中值最大的前k个元素
priority_queue<int, vector<int>, greater<int>> minheap;// 前5个元素入堆for (int i = 0; i < 5; i++){minheap.push(vec[i]);}// 遍历剩余元素,直到最后for (int i = 5; i < vec.size(); i++){if (minheap.top() < vec[i]){minheap.pop();minheap.push(vec[i]);}}// 输出结果 while (!minheap.empty()){cout << minheap.top() << " ";minheap.pop();}2 快排分割法
背景: 实际工作场景中经常遇到求topk的问题,比如找出最近人们搜索最多的商品,最多的应用等,多属于topk的问题,除了上面的利用大小根堆来求解topk问题之外,还可以利用快速排序思想求解topk问题。
**算法思想:**利用快速排序算法思想,判断快排分割函数每次返回的Pos值,如果pos值等于topk就直接返回,这样数组中从0到pos位置求出的就是前topk;如果pos大于或者小于topk,就继续求解。
算法步骤:
利用了快速排序的步骤。


算法性能分析:
平均时间复杂度:第一次找出一半的元素,第二次递归分割直达pos = K-1 ;一共N个元素,平均结果如下:
O(n)=N + N/2 +N/4 + … + 1 = 2N = O(n)
**最坏情况下时间复杂度:如果原始数列是有序的,比如从小到大的排列的,这时候求最大的top1时候,时间复杂度如下:
N +(N-1) + (N-2) +(N -3) + … + 1 = O(N2)=**O(n2)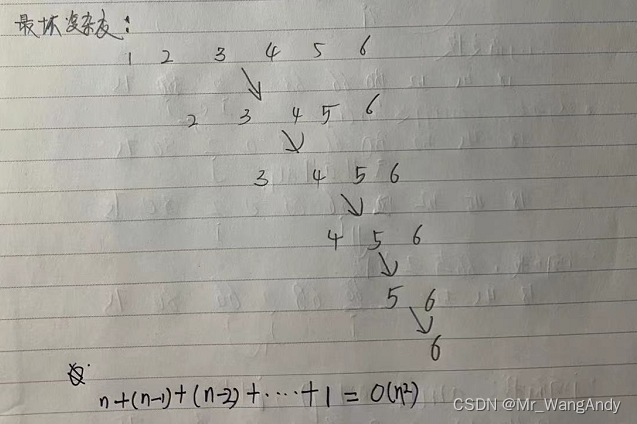
代码
#include <iostream>#include <functional>#include <time.h>using namespace std;/** 功能:快排分割函数。每次递归时,将数组中的数据分割为两组,分别比val大的分成一组,比val小的分成一组。** 参数:*arr[]: 要分割的数组*begin: 数组开始下标*end : 数组的结束位置*/int Partition(int arr[], int begin, int end){int val = arr[begin];int i = begin;int j = end;while (i < j){while (i < j && arr[j] > val){j--;}// 如果找到右边的值大于begin,就进行下面的操作,把比val大的放在if (i < j){arr[i] = arr[j];i++;}while (i < j && arr[i] < val){i++;}if (i < j){arr[j] = arr[i];j--;}}arr[i] = val;return i;}/** 功能:求出前topk** 参数:**arr : 求topk的数组*begin: 数组开始下标*end : 数组的结束位置*k : 要求解的前topk。*/void SelectTopK(int *arr, int begin, int end ,int k){int pos = Partition(arr, begin, end);if (pos == k - 1) // 如果上面分割好的pos中间位置,刚好等于topk,直接返回。{return;}else if (pos > k - 1) // 假如返回 5 而要找topk=3,则继续快排分割。{SelectTopK(arr, begin, pos - 1, k);}else{SelectTopK(arr, begin, pos - 1, k);}}int main(){int arr[] = { 64,45,52,80,66,68,0,2,18,75 };int size = sizeof arr / sizeof arr[0];// 假如求最小的topK,最后返回数组中的topk个元素。int k = 3;SelectTopK(arr, 0, size - 1,k);for (int i = 0; i < k; i++){cout << arr[i] << " ";}cout << endl;system("pause");return 0;}