目录
传统艺能?问题背景?思路?代码实现?
传统艺能?
小编是双非本科大二菜鸟不赘述,欢迎米娜桑来指点江山哦
1319365055
??非科班转码社区诚邀您入驻??
小伙伴们,满怀希望,所向披靡,打码一路向北
一个人的单打独斗不如一群人的砥砺前行
这是和梦想合伙人组建的社区,诚邀各位有志之士的加入!!
社区用户好文均加精(“标兵”文章字数2000+加精,“达人”文章字数1500+加精)
直达: 社区链接点我

问题背景?
由多个节点多个链接的边组成的图,图中某个顶点出发到达另外一个顶点的所经过的边的权重最小的一条路径(权重代表该路径长度),称为 最短路径 \color{red} {最短路径} 最短路径
解决这类问题有 3 种算法:
Dijkstra算法(迪杰斯特拉算法)
Floyd算法(弗洛伊德算法)
SPFA算法
dj 算法是非常常见且面试题出场率比较高的,但是缺点就是不支持负数权重,且下一次查找的方向不确定,算法的特点就是使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树,该算法常作为路由算法或其他图算法的一个子模块
思路?
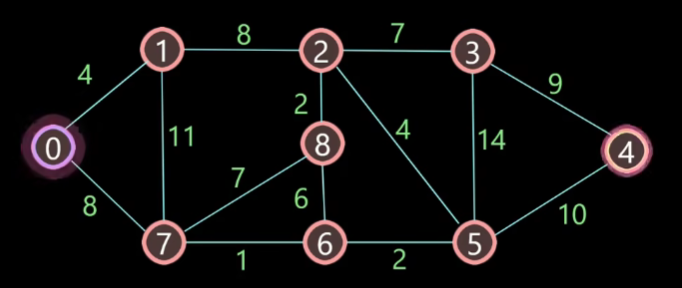
比如要计算节点 0 到节点 4 的最短路径,最短路径采取贪心算法的策略,我们假设某一点无法到达的路径的长度是 ∞ 大,则初始化时所有点我们都初始化为 ∞
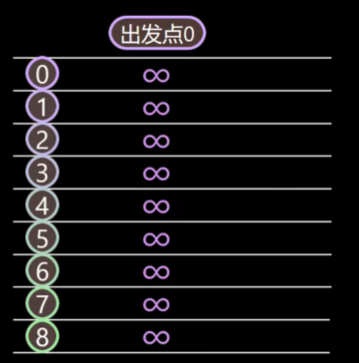
首先节点 0 自己到自己距离一定是 0,所以 0 节点的值覆盖为 0,然后找到所有节点中距离最小的节点,没错就是我自己,于是将 0 标记为最短路径中的节点 。
接着更新 0 节点的邻接节点 1 和 7 的距离,他们的权重是 4 和 8,因为小于 ∞ 路径长更新为4,8,此时节点 1 和节点 7 的前面节点就是节点 0,这个过程有个专业术语叫做“松弛”,即 v0 顶点到 v1 顶点的路程即 dis[1] = 4,通过 <v0,v1> 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛v1顶点到其余各个顶点的路程
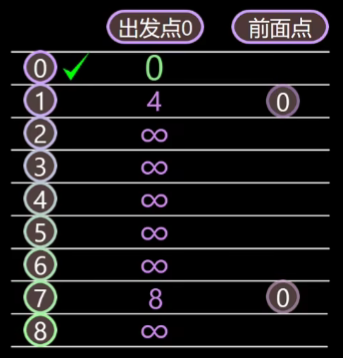
接着又从未标记节点中,即剩下节点中找到距离出发点最小的节点,是节点 1 ,然后标记节点 1 为最短路径中的节点。继续更新节点 1 的邻接节点 2 和 7
首先节点 1 到节点节点 2 的距离是 8,从 0 开始的路径 v0–v1–v2 的长度就是 12,此时更新节点 2 的距离就是 12,他的前面点是节点 1;同理另一条路径 v0–v1–v7 路径长 15 ,因为这个路径要大于 7 本来的距离(8),所以不更新
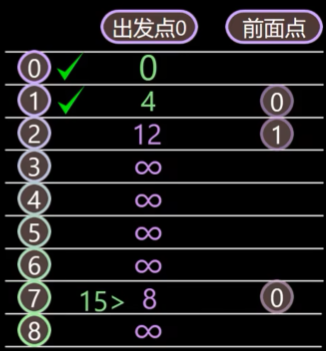
继续在剩下节点中寻找最小节点,就是节点 7 ,把节点 7 放进最短路径节点,接着更新 7 的邻接节点:节点 8 和节点 6。v0–v7–v8 长度为 15,v0–v7–v6 长度为 9,此时他们都比 ∞ 小进行更新,他们前面点都是节点 7。
重复如上步骤就是本算法的核心思想,其实我们细看的话就分为两步:
每次从未标记节点选出最小值节点,标记到最小路径集合中计算刚加入的最小值节点 A 到某个邻接节点 B 的距离,即 A (此时 A 已经包含了之前路径的和)+ A 到 B 的距离,如果结果小于 B 本身的距离,就更新 B 的值和前面点循环这个过程,直到终点被标记。寻着这个规律,我们把剩下的路走完来演示一下:
在未标记节点中找到最小节点 6,标记为最小路径中的节点,找到 6 的邻接节点:节点 8 和节点 5,v0–v7–v6–v5 路径长为 11,小于 ∞ 因此进行更新;v0–v7–v6–v8 路径长为 15,和原来一样就不做更新了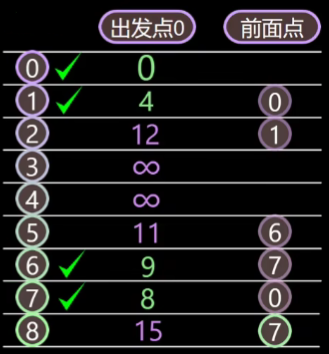
接着寻找最短距离节点,是 5 进行标记放入最短路径点集合,这时他的邻接节点有三个: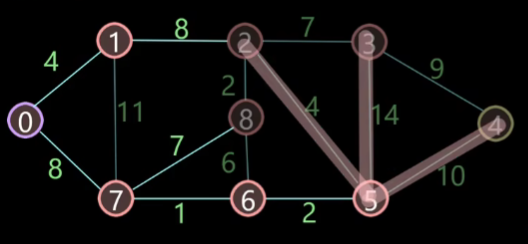
经过计算,节点 2,3,4 的路径长为 15,25,21,因为原来 2 节点为 12,所以不进行更新,而 3,4 节点更新成为 25,21。
那么接下来最短节点就是 2,他的邻接节点是节点 8 和节点 3,节点 5 因为标记过了,所以不需要标记节点 5 了,路径 v2–v3 长度 19,路径 v2–v5 长度 14,两个路径都要更新距离和前面点。
接下来最短距离节点是 8,他的邻接节点都已经被标记,无需更新;然后最短距离节点就是 3,更新未被标记的邻接节点 4,v3–v4 的路径长度为 28,28 大于当前本身的 21,所以不做更新。
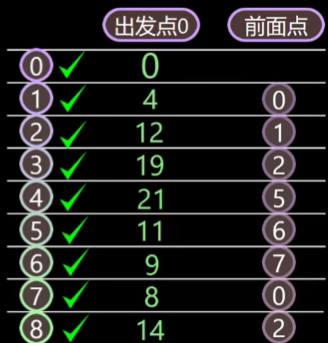
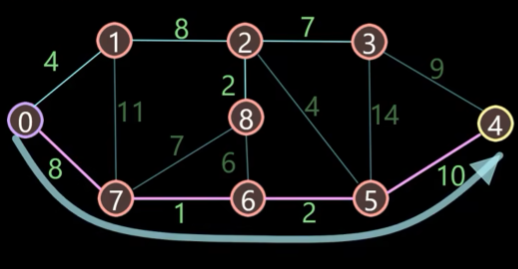
最后将未被标记的节点 4 标记,更新完毕,得出结论:从出发点 0 开始目的地节点 4 节点的最短距离就是 21
此时的最短路径就是将上麦很从上到下的前面点一一链接起来即可:
代码实现?
此时我们初始化一个数组 dis 来保存起点到各个点的最短距离和一个保存已经找到了最短路径的点(或者称之为前面点)的集合即可
void Graph_DG::Dijkstra(int begin){ //初始化 dis 数组 int i; for (i = 0; i < this->vexnum; i++) { //设置当前的路径 dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1); dis[i].value = arc[begin - 1][i]; } //设置起点的到起点的路径为0 dis[begin - 1].value = 0; dis[begin - 1].visit = true; int count = 1; //计算剩余的顶点的最短路径(剩余this->vexnum-1个顶点) while (count != this->vexnum) { //temp用于保存当前dis数组中最小的那个下标 //min记录的当前的最小值 int temp=0; int min = INT_MAX; for (i = 0; i < this->vexnum; i++) { if (!dis[i].visit && dis[i].value<min) { min = dis[i].value; temp = i; } } //cout << temp + 1 << " "<<min << endl; //把temp对应的顶点加入到已经找到的最短路径的集合中 dis[temp].visit = true; ++count; for (i = 0; i < this->vexnum; i++) { //注意这里的条件判断INT_MAX必须加,不然会出现溢出异常 if (!dis[i].visit && arc[temp][i]!=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) { //如果新得到的边可以影响其他的顶点,那就更新它的最短路径和长度 dis[i].value = dis[temp].value + arc[temp][i]; dis[i].path = dis[temp].path + "-->v" + to_string(i + 1); } } }将本文的方法具体迁移到代码上如果有不太理解的,推荐看看这篇博客,方法都是一样的,这位博主直接用的 dis 数组查询过程进行论证:Dijkstra算法