?‍?作者简介：一位喜欢写作，计科专业大二菜鸟

?个人主页：starry陆离

?首发日期：2022年5月31日星期二

?上期文章：动态规划:多重背包问题

?订阅专栏：算法分析与设计
如果文章有帮到你的话记得点赞?+收藏?支持一下哦

贪心算法：最小生成树Prim算法

笔者前言1.问题引入2.最小生成树3.设计思路4.图解算法5.完整代码

---

笔者前言

这是大一暑假的c笔记，再一次写prim算法笔记又有一点点进步
最小生成树（Prim普利姆算法和Kruskal算法）

1.问题引入

若要将n个城市之间原有的公路改造为 高速公路，这些城市之间原有公路网 如图所示，每条边上的数字表示高 速公路的改造成本（单位：10亿元）。 如何以最低的成本来构建高速公路网， 使得任意两个城市之间都有高速公路 相连？

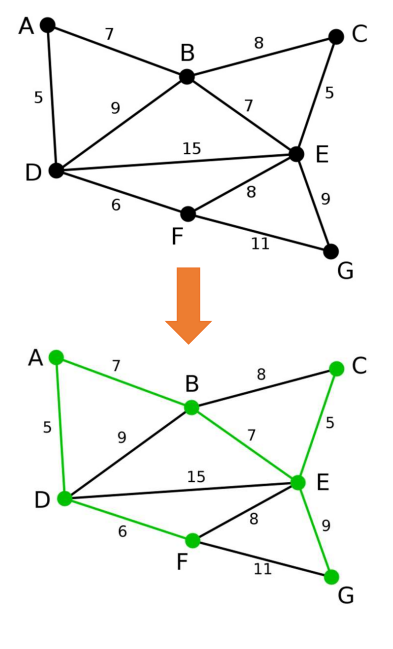
2.最小生成树

Minimal Spanning Trees (MST)

任何只由图G的边构成，并包含G的所有顶点的树称为G的生成树加权无向图G的生成树的权重是该生成树的所有边的权重之和最小生成树是其所有生成树中权重最小的生成树N个顶点，选取N-1条边，构建一个连通图，且这N-1条边的权重之和最小

3.设计思路

任意选定一点s，设集合S={s} （Prim算法的特点从点出发）

从不在集合S的点中选出一个点j使得其与S内的某点i的距离最短，则(i，j) 就是生成树上的一条边，同时将j点加入S

转到(2)继续进行，直至所有点都己加入S集合，所以一棵有n个顶点的图构成的最小生成树有n-1条边

因此我们设计这个算法时需要保存的信息有：

数组e[][]来记录图的各边权重数组visited[j]来保存当前节点j是否被访问（是否在集合s中）数组dis[j]记录不在集合S的点中的节点j与S内的某点i的距离最短距离数组close[j]记录顶点j的最近邻接点

4.图解算法

首先我们要储存这张图，用一个二维数组e[][]即可，并且初始化时这个图上各点的距离应该为无穷大，表示各点没有连通

//初始化各边均不相邻for(int i=0;i<n;++i) {    for(int j=0;j<n;++j) {        e[i][j]=Integer.MAX_VALUE;    }}//录入各边的信息int x,y;for(int i=0;i<m;++i) {    x=scanner.nextInt();    y=scanner.nextInt();    e[x][y]=scanner.nextInt();    e[y][x]=e[x][y];//可别忘了这一行哦，无向图的存储}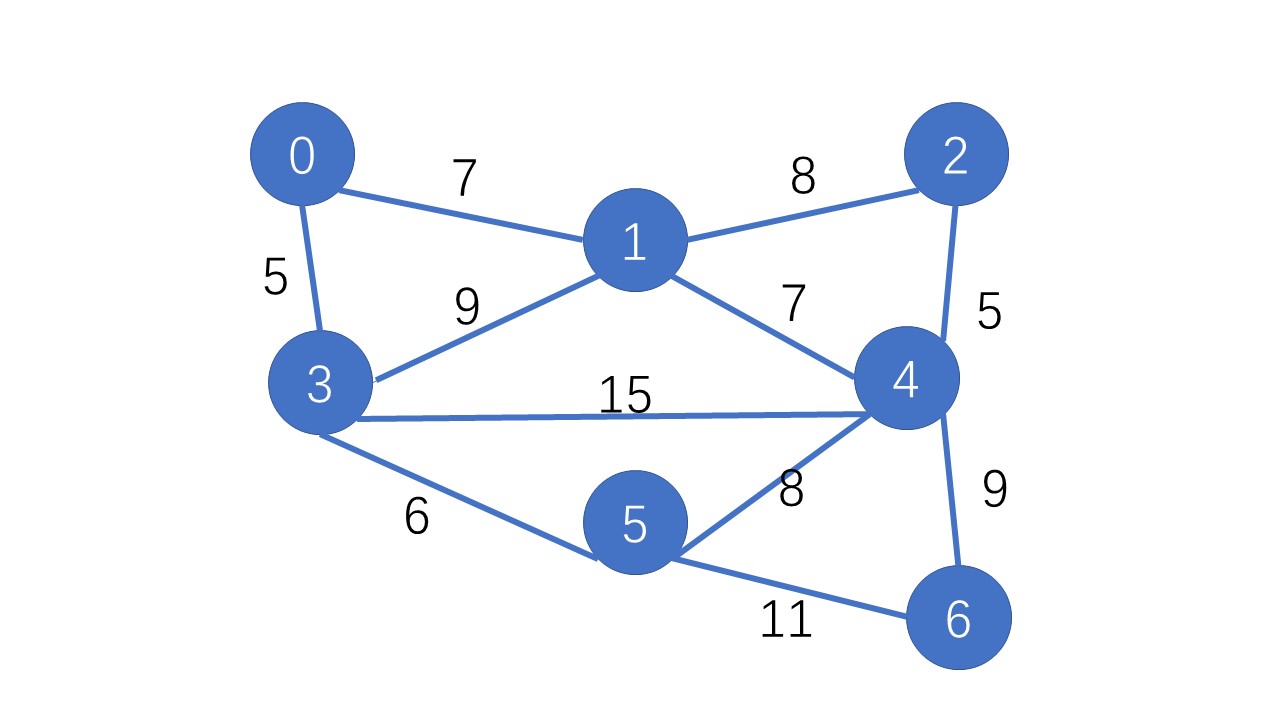

其次我们任选一点，一般都是从最小的顶点开始，如0点；将其加入集合S中，这时要做的操作就多着，首先要获取其他顶点到第1个点(0)的距离，不直接相邻的顶点距离为无穷大；其次初始化所有点的最近邻接点都为第1个点(0)；最后还要将第1个点加到S中，更新visited[0]=1;

//初始化，S中只有第1个点(0)    for(int i=0;i<n;++i) {        dis[i]=e[0][i];//获取其他顶点到第1个点(0)的距离，不直接相邻的顶点距离为无穷大        close[i]=0;//初始情况下所有点的最近邻接点都为第1个点(0)        visited[i]=0;//初始情况下所有点都没有被访问过    }    visited[0]=1; //访问第1个点(0)，将第1个点加到S中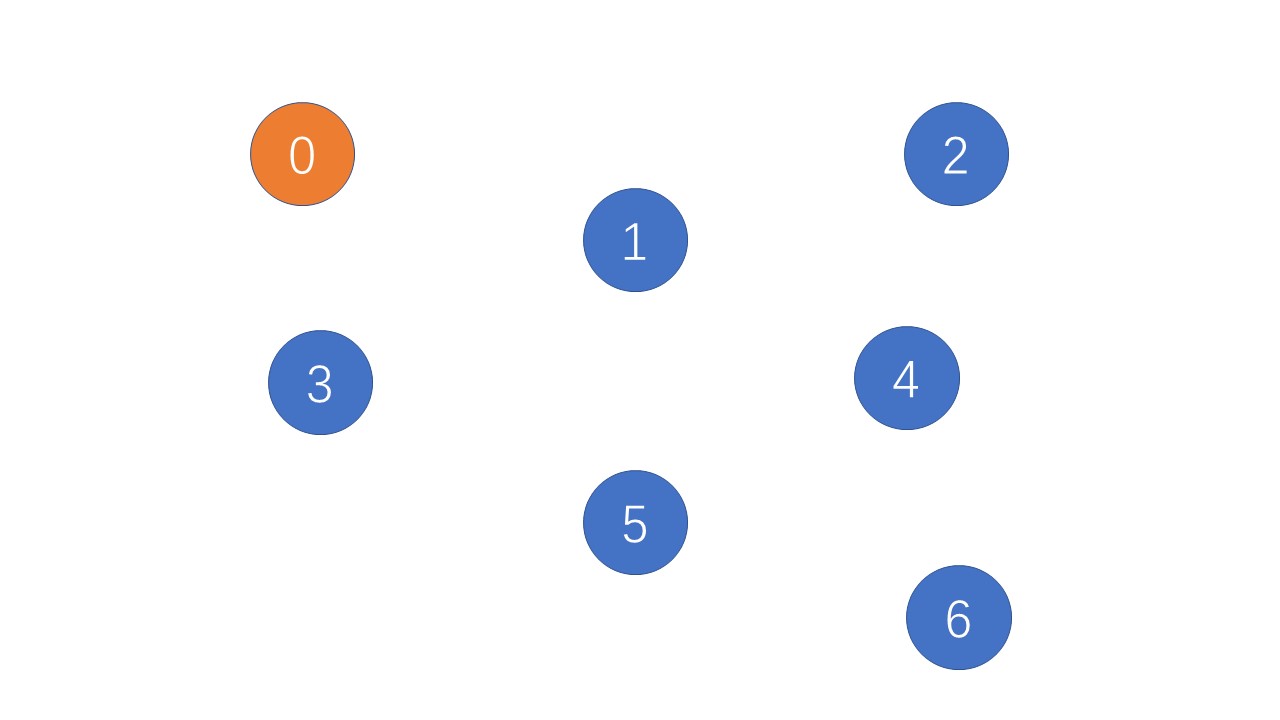

接下来要做的事就头大了。我们要遍历剩下的所有点，直到所有的点都加入到集合S中，慢慢来我们一个一个加。所要做的操作就是：

从不在集合S的点中选出一个点j使得其与S内的某点i的距离最短，则(i，j) 就是生成树上的一条边，同时将j点加入S

这时集合S中只有一个点（0），那么遍历找到不再集合S中的其他点到点（0）的最小的距离，我们发现是点（0）和点（3）最近，距离为5；用一个遍历index记录这个点，并更新visited[3]=1表示将点（3）加入到集合S中

int index=0;//如果顶点k没有被使用，且到S的距//离小于k到S的距离，将k赋给index for(int k=0;k<n;++k) {    if(visited[k]==0&&dis[k]<dis[index]) {        index=k;//记录到S距离最小的顶点    }}//将顶点index加入集合S并更新dis[]数组visited[index]=1;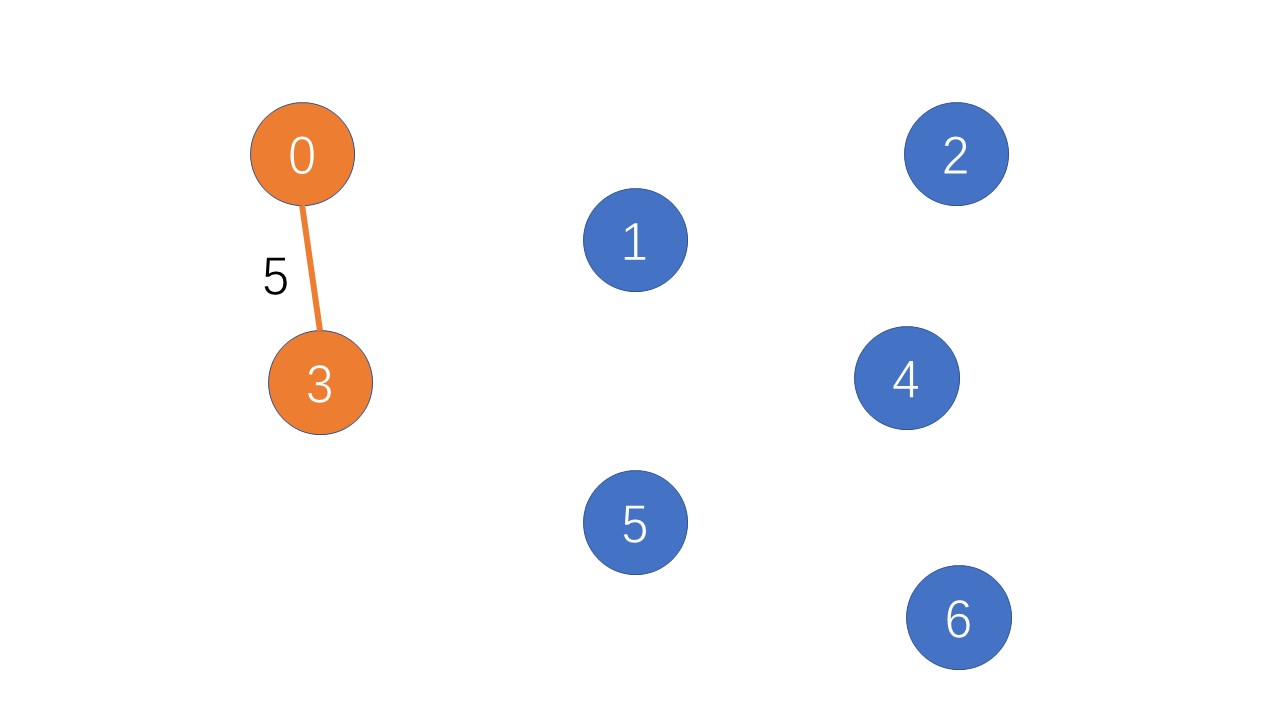

这可没完，我们把新的顶点（3）加入到了集合S中，那么不在集合S中的点到集合S中的点的距离就应该更新。举个例子：

在点（3）没加入集合S前，S={0}，点（5）到集合S的最小距离为无穷大，dis[5]=MAX在点（3）加入集合S后，S={0,3}，点（5）到集合S的最小距离就是点（3）到点（5）的距离，dis[5]=6

除此之外我们还应当记录下close[5]=3，表示点（3）作为点（5）到S中的最近邻点

//每一次循环用于在index加入S后，重新计算不在S中的顶点到S的距离，修改与index相邻的边//到S的距离，即更新dis和close    for(int k=0;k<n;++k) {        //松弛操作，如果k没有被使用，且k到index的距离比原来k到S的距离小        if(visited[k]==0&&dis[k]>e[index][k]) {            dis[k]=e[index][k];//将k到index的距离作为新的k到S之间的距离            close[k]=index;//将index作为k在S中的最近邻点        }    }

然后就套用一个循环，从点（1）找到点（n）；不多说了直接看图

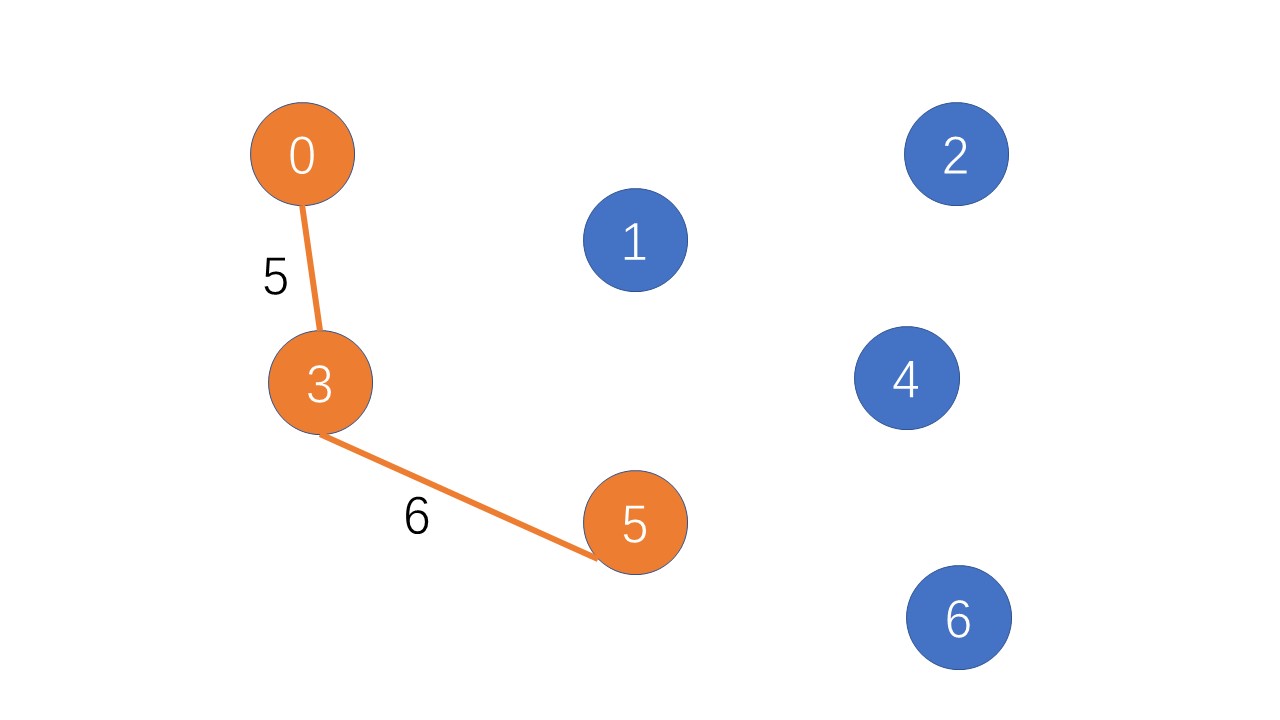
找到第四个点：

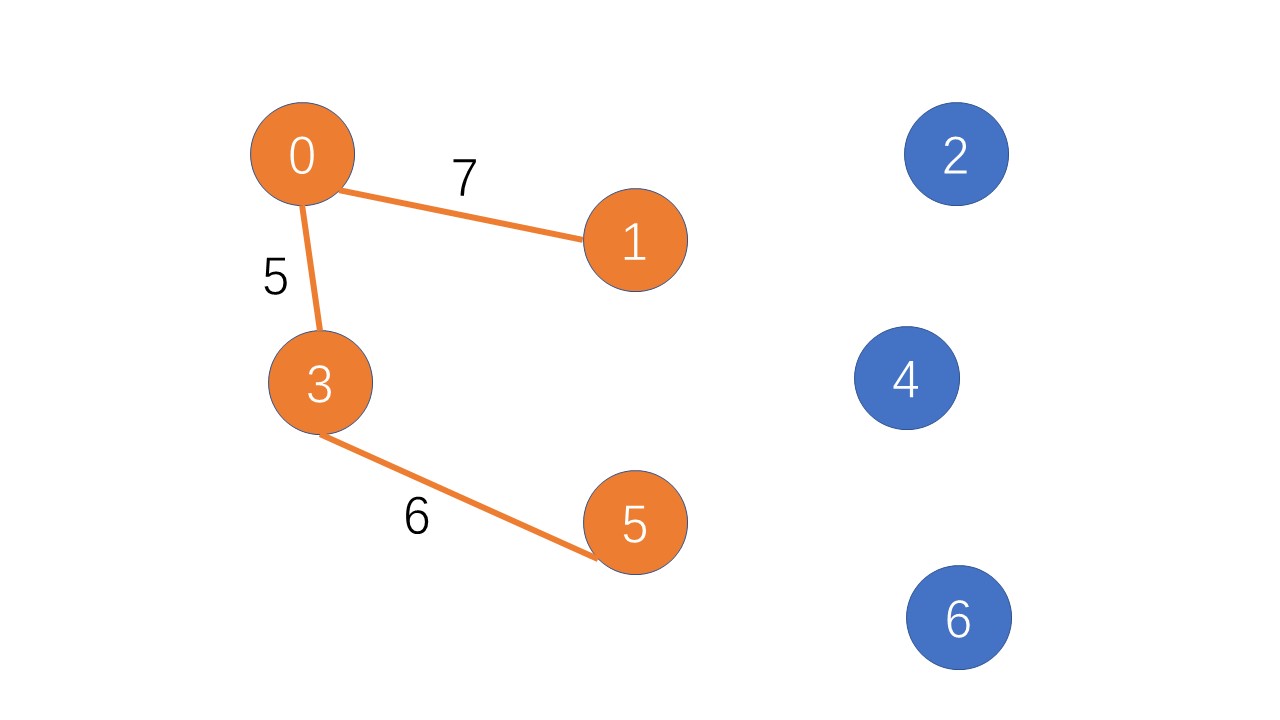
找到第五个点：

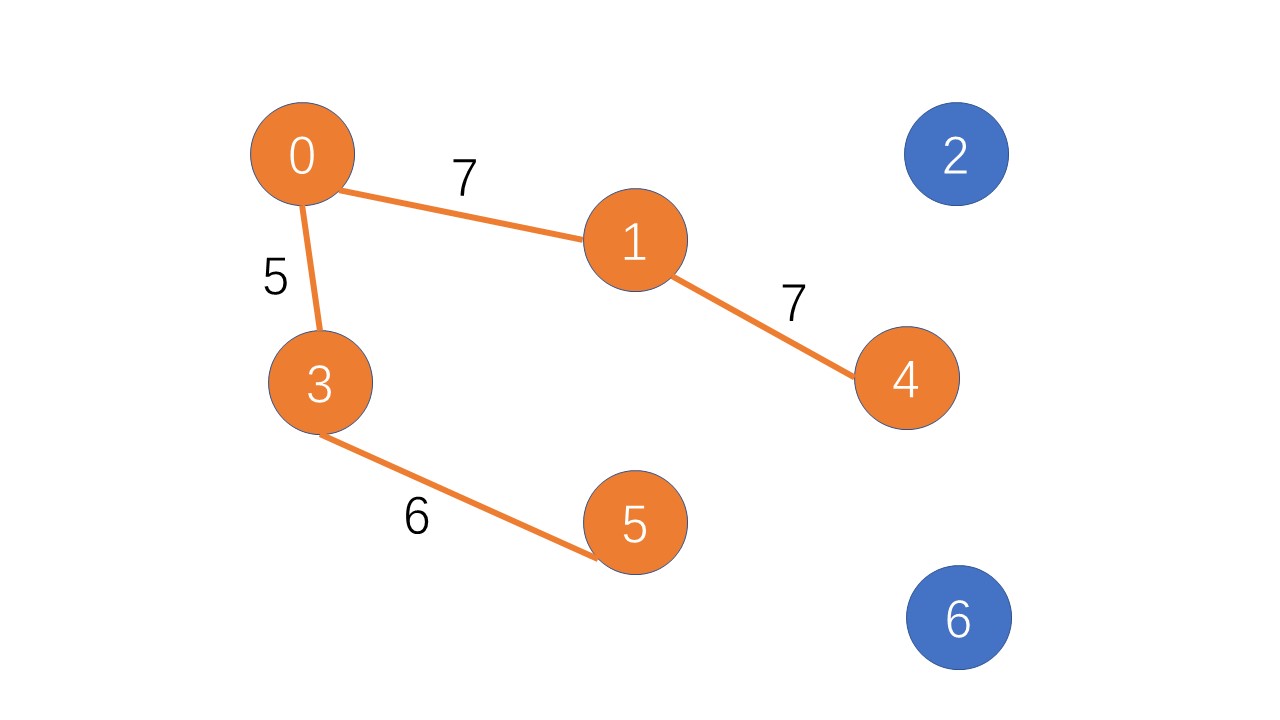
找到第六个点：

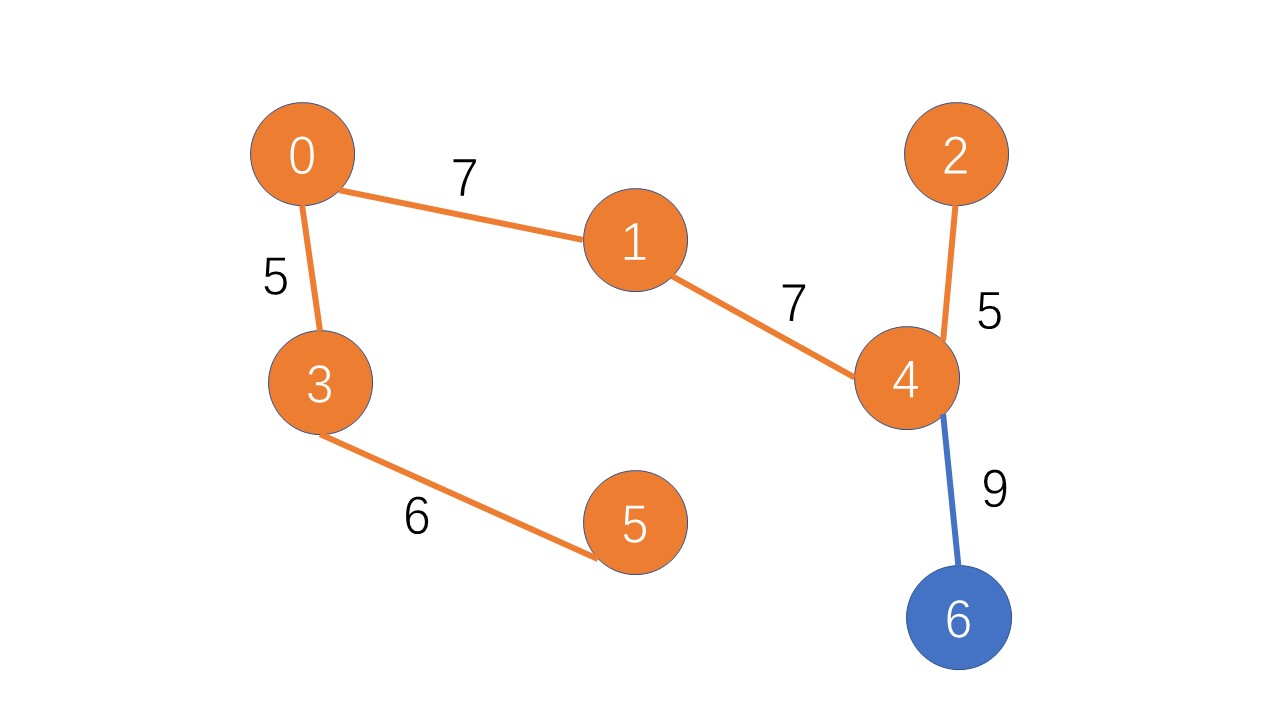
找到第七个点：找全啦，正好7-1=6条边

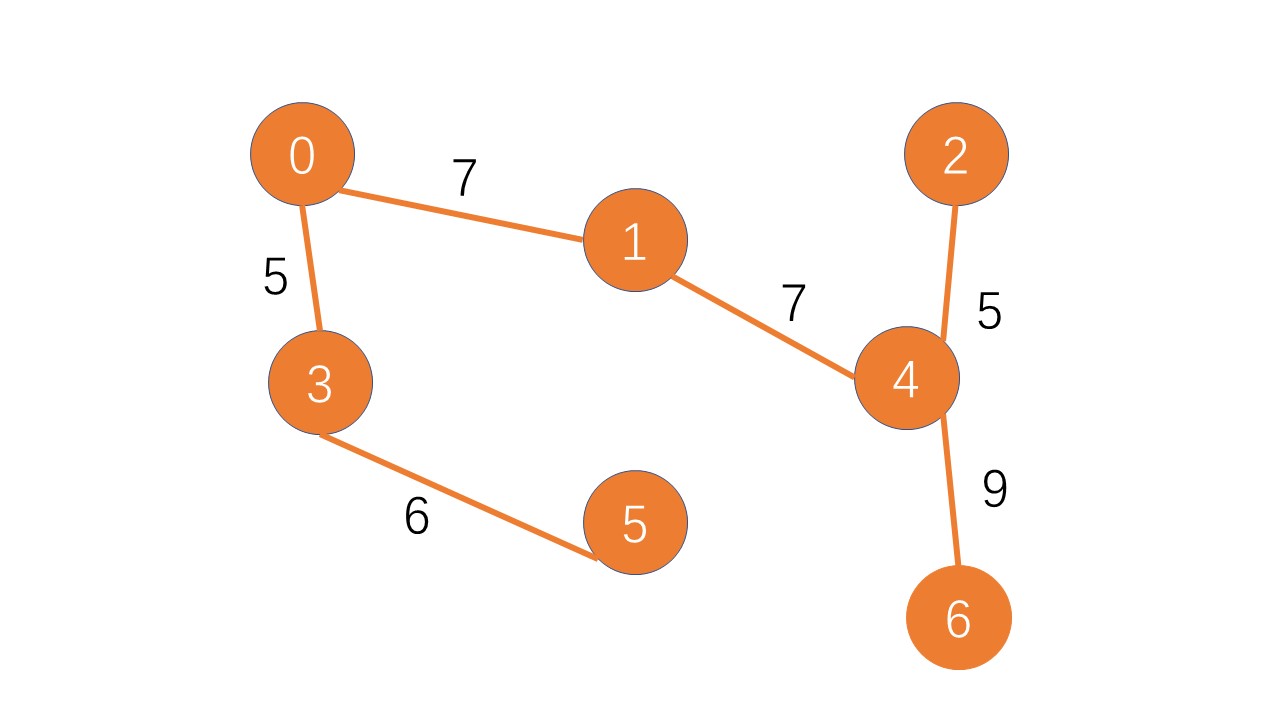
5.完整代码

import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n,m;//点和边int e[][];//储存权值int dis[];//记录最小权值int visited[];//记录当前点是否加入集合Sint close[];//记录邻接点while(scanner.hasNext()) {n=scanner.nextInt();//点m=scanner.nextInt();//边e=new int[n][n];dis=new int[n];visited=new int[n];close=new int[n];//初始化各边均不相邻for(int i=0;i<n;++i) {for(int j=0;j<n;++j) {e[i][j]=Integer.MAX_VALUE;}}//录入各边的信息int x,y;for(int i=0;i<m;++i) {x=scanner.nextInt();y=scanner.nextInt();e[x][y]=scanner.nextInt();e[y][x]=e[x][y];//可别忘了这一行哦，无向图的存储}//初始化，S中只有第1个点(0)for(int i=0;i<n;++i) {dis[i]=e[0][i];//获取其他顶点到第1个点(0)的距离，不直接相邻的顶点距离为无穷大close[i]=0;//初始情况下所有点的最近邻接点都为第1个点(0)visited[i]=0;//初始情况下所有点都没有被访问过}visited[0]=1; //访问第1个点(0)，将第1个点加到S中for(int i=1;i<n;++i) {int index=0;//如果顶点k没有被使用，且到S的距//离小于k到S的距离，将k赋给index for(int k=0;k<n;++k) {if(visited[k]==0&&dis[k]<dis[index]) {index=k;//记录到S距离最小的顶点}}//输出构成最小生成树的每条边System.out.println(close[index]+" "+index+" "+dis[index]);//将顶点index加入集合S并更新dis[]数组visited[index]=1;//每一次循环用于在index加入S后，重新计算不在S中的顶点到S的距离，修改与index相邻的边//到S的距离，即更新dis和closefor(int k=0;k<n;++k) {//松弛操作，如果k没有被使用，且k到index的距离比原来k到S的距离小if(visited[k]==0&&dis[k]>e[index][k]) {dis[k]=e[index][k];//将k到index的距离作为新的k到S之间的距离close[k]=index;//将index作为k在S中的最近邻点}}}}scanner.close();}}

测试案例：

7 110 1 70 3 51 2 81 3 91 4 72 4 53 4 153 5 64 5 84 6 95 6 11

样例输出：

0 3 53 5 60 1 71 4 74 2 54 6 9