目录
构造链式二叉树
创建一颗二叉树
二叉树的遍历
前序遍历
中序遍历
后序遍历
层序遍历
判断二叉树是否为完全二叉树
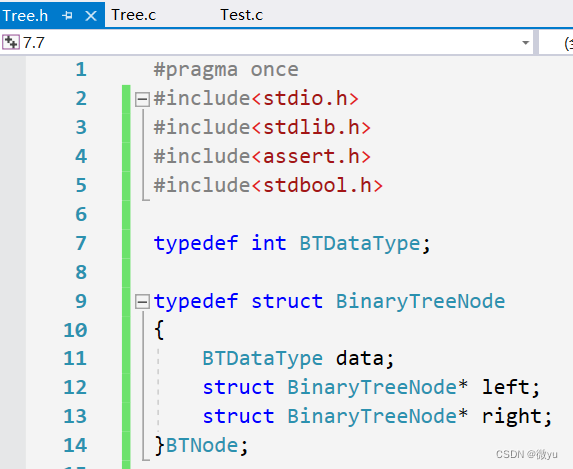
节点个数以及高度
二叉树节点个数
二叉树叶子节点个数
二叉树的高度
二叉树第k层节点个数
二叉树查找值为x的节点
二叉树的创建和销毁
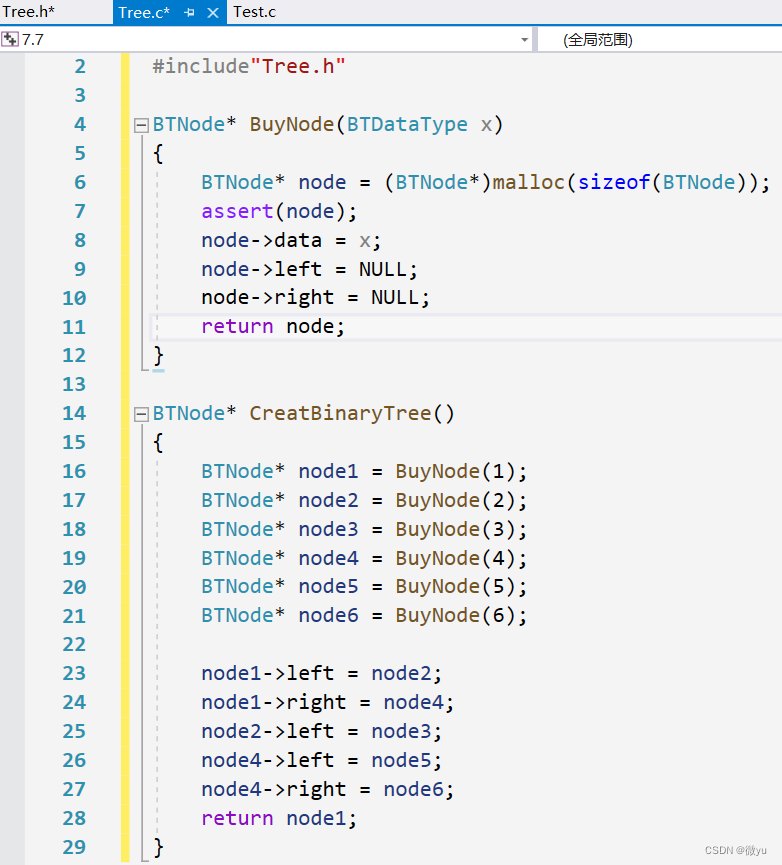
创建
销毁
结语
构造链式二叉树
上一篇博客介绍了堆,堆是用数组来实现的,通过控制数组下标来实现各种功能,那这一篇就通过链式二叉树来了解一下二叉树吧。
链式二叉树,和之前的链表似的,只不过一个节点有两条链
创建一颗二叉树
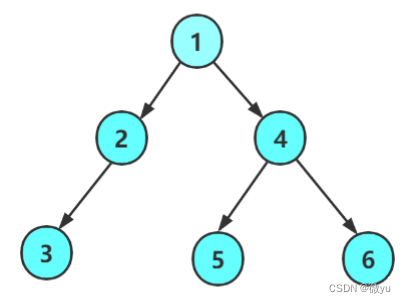
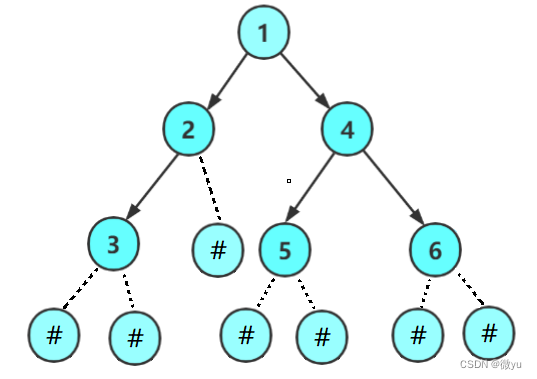
为了方便介绍二叉树,先来 “手搓” 一个二叉树,通过这个简单的二叉树来了解二叉树的性质,但这并不是创建二叉树的方式。
这就是这棵树的结构
二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
遍历的方式分为:前序遍历、中序遍历和后序遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。 2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。 3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。 简单来说: 这里的前中后是针对根节点来说的,抛开这三种遍历顺序,都是按照根、左树、右树的顺序来遍历的。 前序就是先访问根,再左树和右树; 中序就是先访问左树,再访问根,最后访问右树; 后序就是先访问左树和右树,再访问根。
前序遍历
这三种遍历方式都是用递归实现的,为了能看清遍历过程,我们使用打印的方式,只要是空树就打印 “#”,不是就打印对应的数据。

先打印一下前序遍历
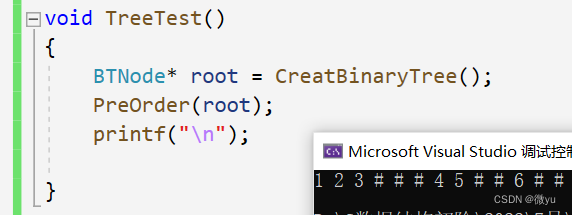
图也可以这样看,下面是默认的空树
这就是完整的递归展开图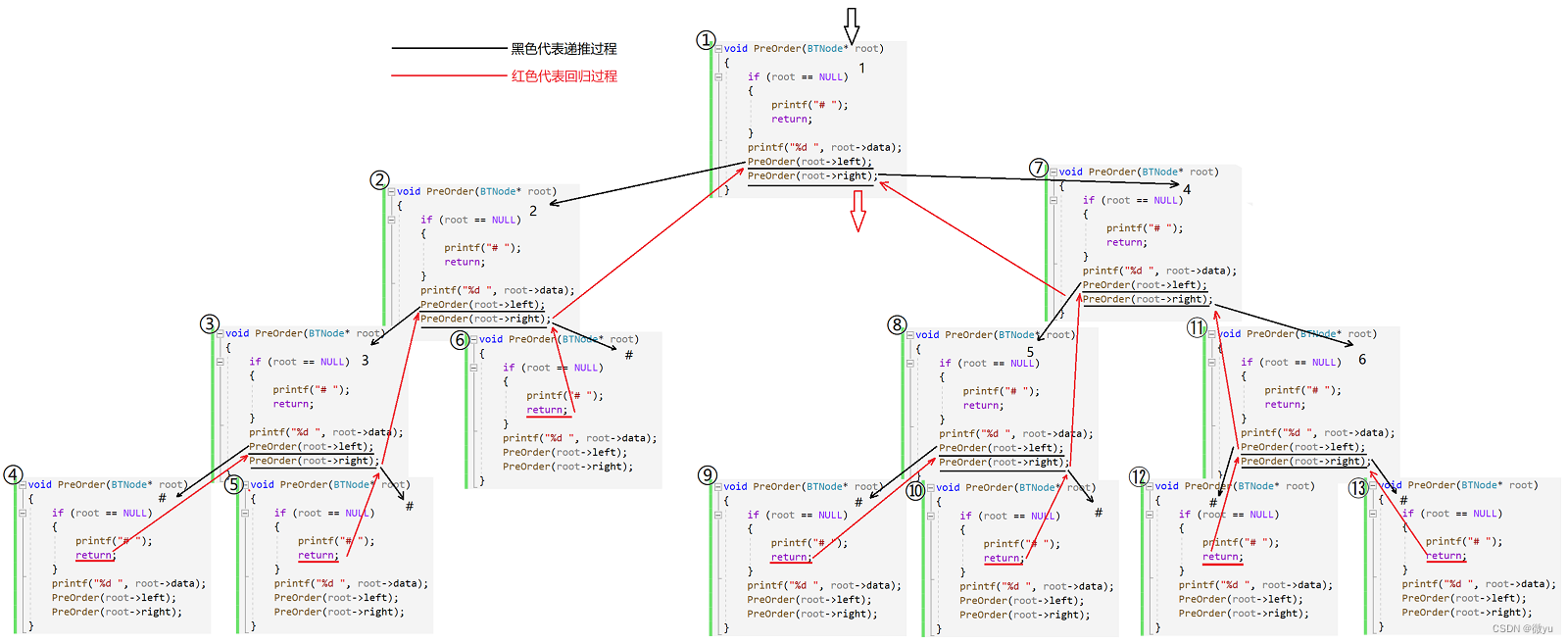
中序遍历

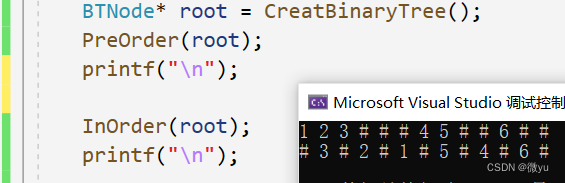
因为中序遍历和后序遍历的递归展开图大同小异,画法差不多,所以可以自己思考一下怎样去画。
后序遍历


层序遍历
层序遍历通常是借助一个队列来实现的,层序遍历是先访问第一层,再第二层,直到最后一层。
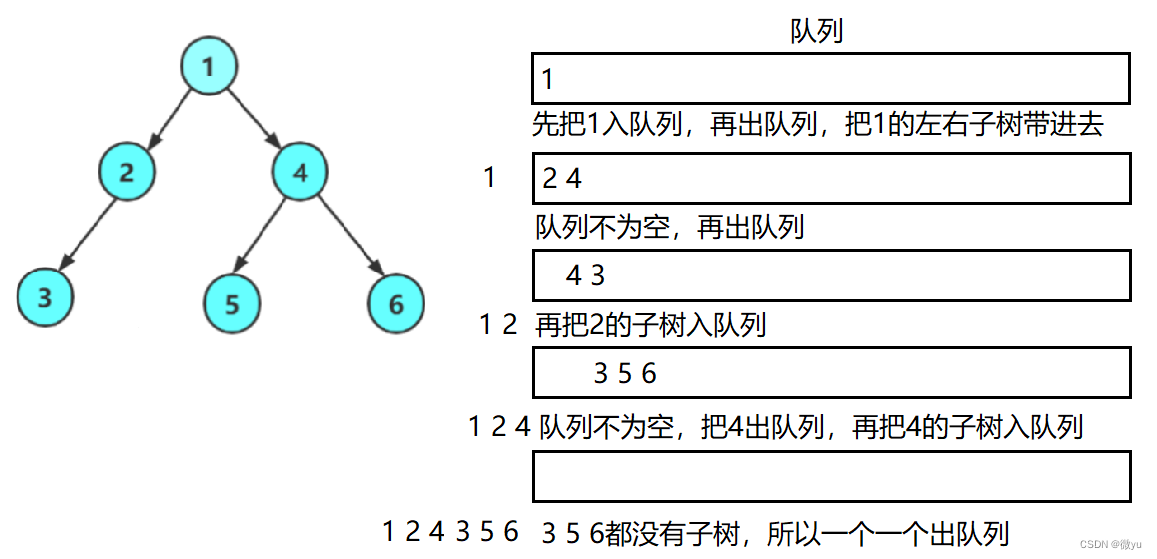
接下来就是得有个队列,由于是用C语言写的,库里没有队列这个数据结构,所以只能拿原来写的队列。
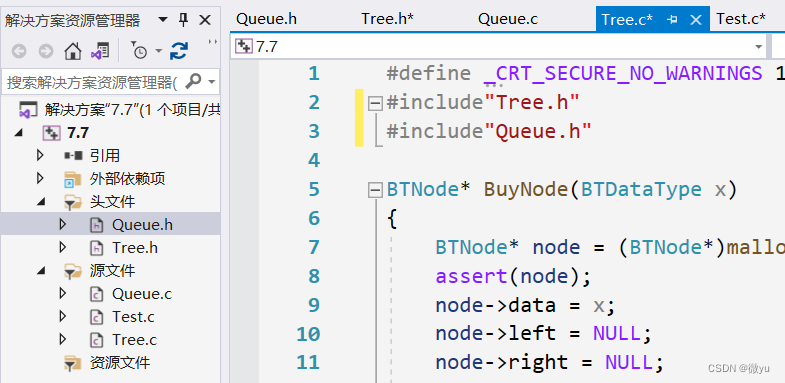
把之前写的队列添加到这里面,再写上队列的头文件。
还有一个问题是,上面讲的思想是把一个节点入队列和出队列,但是队列的每个元素是整型,还需要做一些修改,需要加一个前置声明,为了把队列中的每个元素都变成BTNode*。
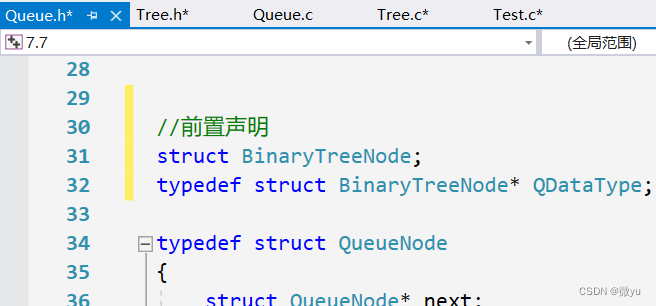
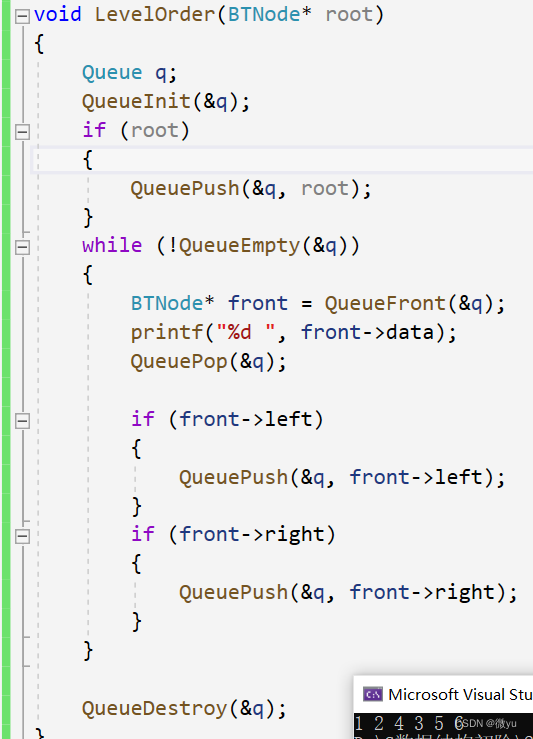
判断二叉树是否为完全二叉树
判断二叉树是不是完全二叉树就可以用层序遍历的方式来判断
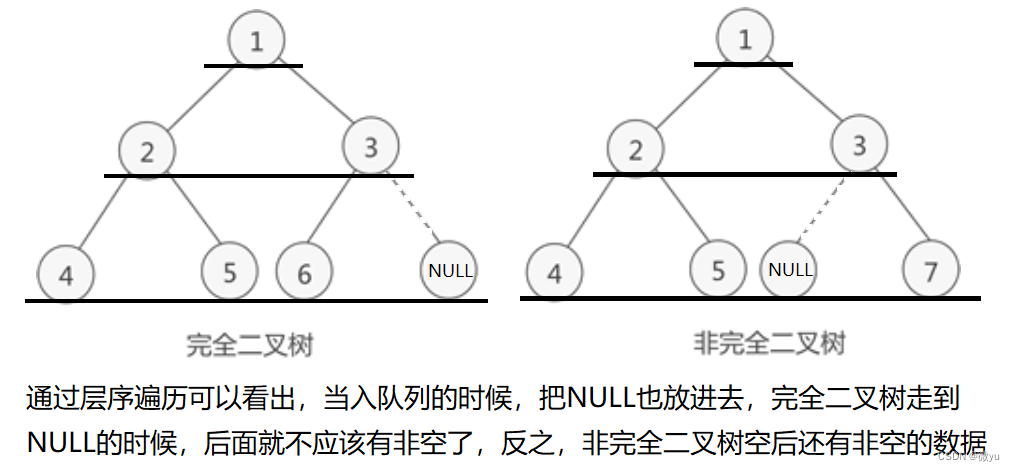

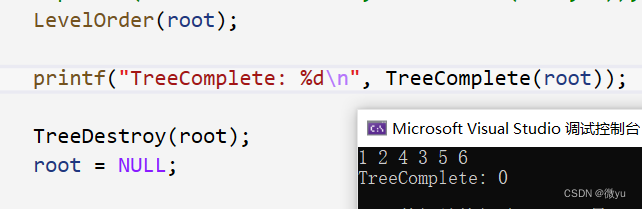
队列销毁的时候一定要在返回之前,不然返回了,队列没有销毁就会造成内存泄漏,虽然不会报错,但还是会存在隐患。
二叉树还是上面的二叉树,所以这不是一个完全二叉树,改一下左右子树就可以看到完全二叉树的结果了。
节点个数以及高度
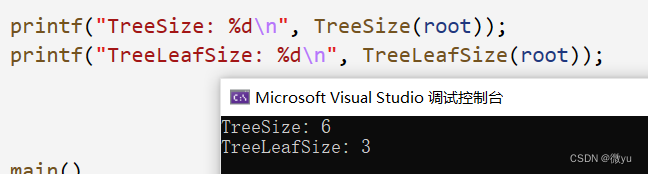
二叉树节点个数
这一小部分想要得到的都是节点个数之类的,那么就要用到分治的思想:
既然想得到整个二叉树的节点个数,每一部分都可以看作是一个左子树,一个右子树,加一个根,那么节点个数就可以认为是:
左子树的节点个数+右子树节点个数+1(根节点)。

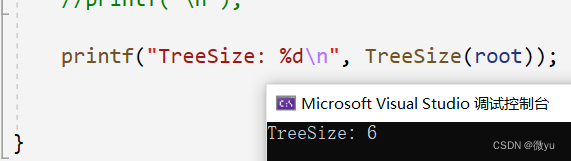
这个代码还可以简化成这样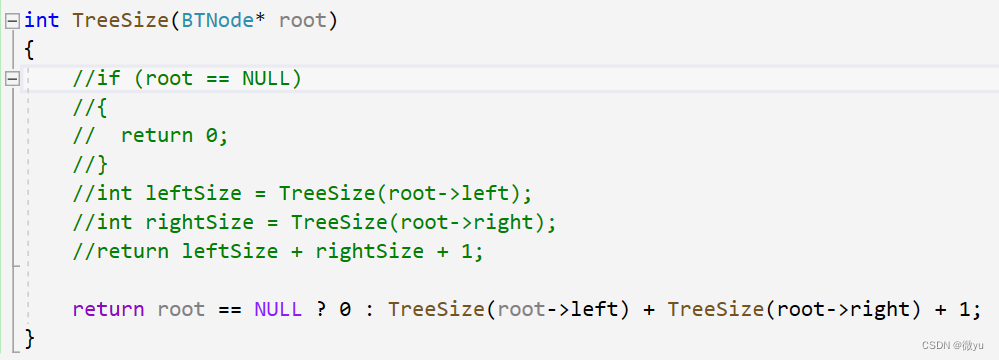
二叉树叶子节点个数
同样是用分治的思想,把左子树的叶子节点个数和右子树的节点个数相加就是整颗二叉树的节点个数;叶子节点的特征就是它的左子树和右子树都是空的,这就可以拿来当作判断条件。

二叉树的高度
同样可以使用分治的思想,只不过不是把左右子树相加了,高度是什么呢,是左右两个子树高度的较大值,比如下面这张图:
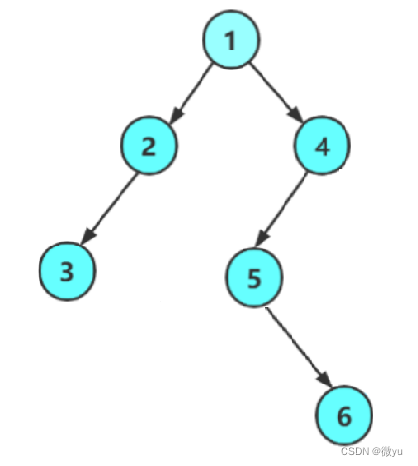
左树的高度是2,右树的高度是3,再加上根节点的那一层,应该高度是4,所以要分治求出两个子树的较大值后再加一才是整个树的高度。

这只是一种写法,也可以把+1写到定义的两个局部变量后;这里建议还是定义两个局部变量,如果不这样写,下面这种也可以。
 这种每次函数栈帧会开辟一块新的空间,不仅时间和空间都会有一定的浪费,所以还是不建议这样写。
这种每次函数栈帧会开辟一块新的空间,不仅时间和空间都会有一定的浪费,所以还是不建议这样写。
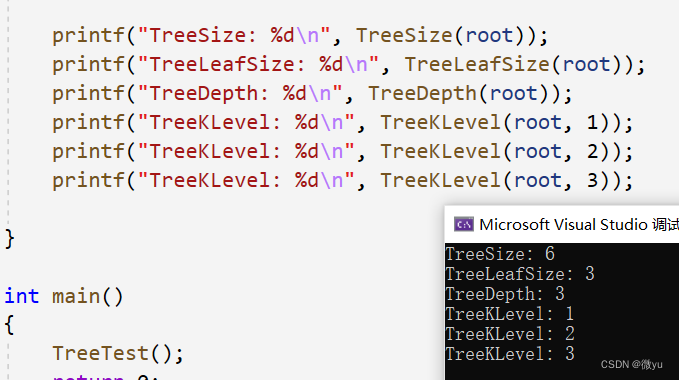
二叉树第k层节点个数
这一部分比较麻烦的就是如何找到第k层,随着递归的深入,想要直到本次递归在第几层也很麻烦。
那想想可不可使用全局变量,建议还是不要这样,第一点,全局变量并不好;第二点,它并不能解决这个问题,每次递归就+1很容易就会出bug。
那这里就介绍另一种方法。
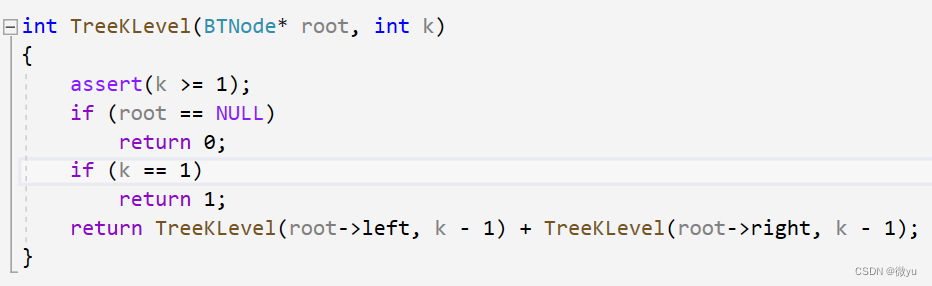
用k表示要找第几层的节点个数,那这个值就得>=1。

二叉树查找值为x的节点
函数的返回类型为BTNode*,所以找到了要把那个节点带回去,如果找到那个节点就打印返回的节点对应的data,如果找不到就返回NULL。
用同样的思想,先看看根节点是不是x,如果是就直接返回了,如果不是就去左树和右树里找,如果在左树中找到了就直接返回了,那就不管右树里有没有了;如果左树找不到,再去右树找;最后左树和右树都没找到,那x就不存在,直接返回NULL就可以了。
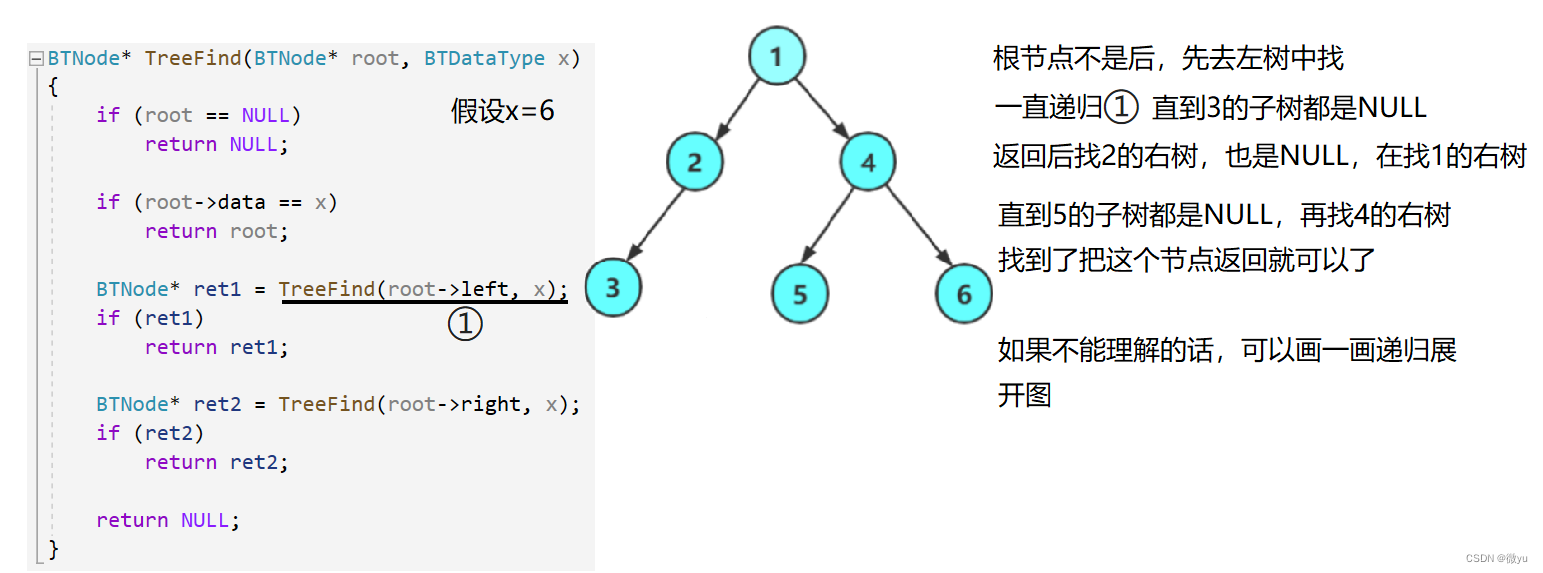
同样的问题,这里找到的返回值最好保存在一个变量中,要不然返回的时候还得再找一遍。
二叉树的创建和销毁
创建
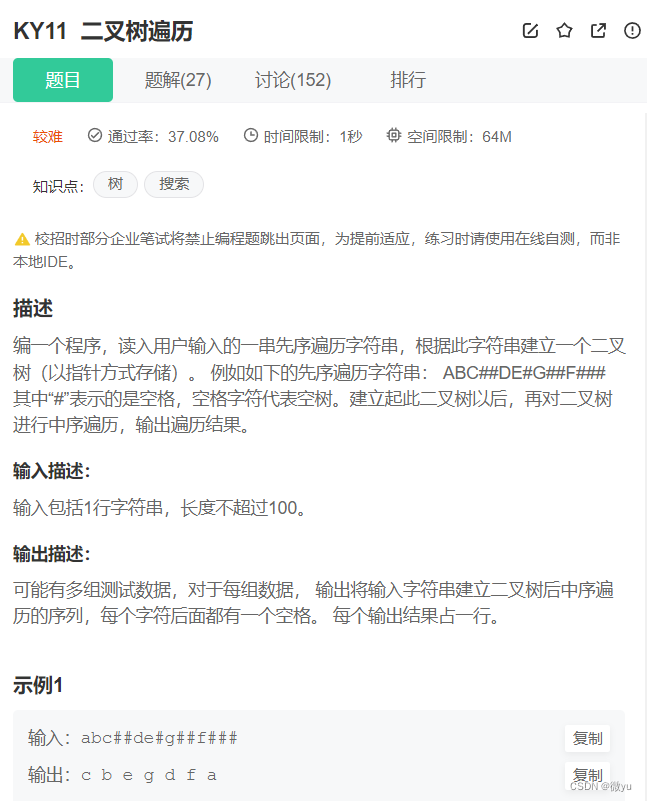
创建的方法可以看一下这道题,输入一个前序遍历字符串来创建二叉树
输入一个字符串,定义一个i,把两个变量的地址传入函数
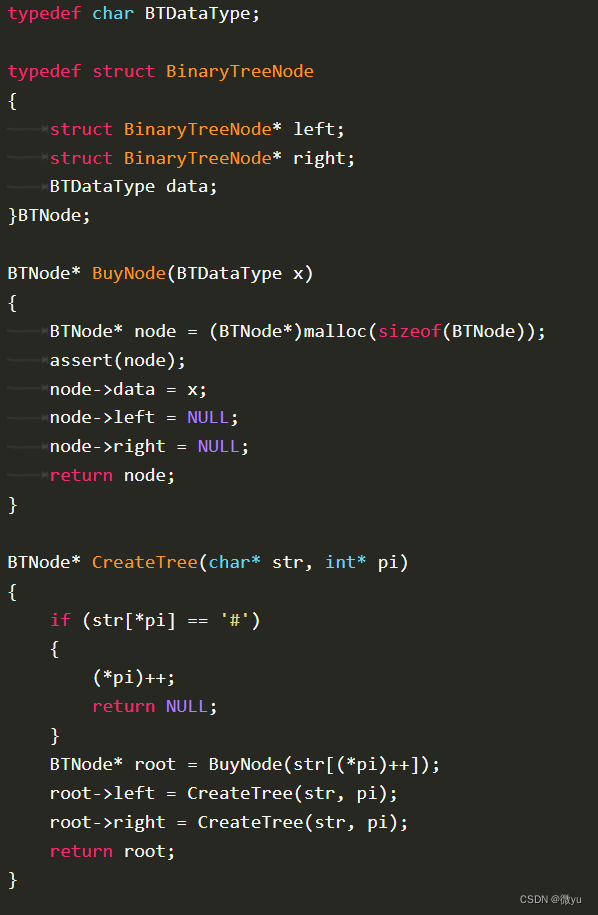
因为是个字符串,要把typedef的int改为char,BuyNode函数不用改。为什么i也要传入地址呢。递归创建二叉树,每放入一个数据,字符串就要往后挪,数组下标就要移动,所以要传入地址。
每放入一个数据都要BuyNode,因为题目说前序遍历的字符串,所以先创建根,再创建左子树和右子树。
最后返回根节点。
销毁
销毁可以有三个方向,前序,中序还有后序,前序就是先释放根节点,再释放左右子树,但是释放了根就找不到左右子树了;所以就可以使用后序的方法,先把左右子树都释放了,再释放根。

为了看出释放的顺序可以加一行
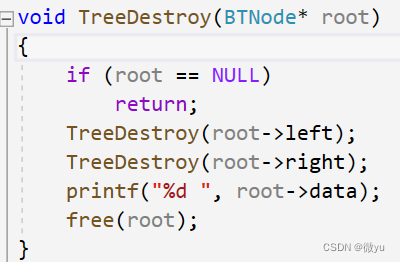
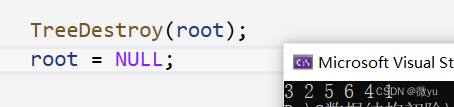
可以看到释放的顺序就是后序。
结语
二叉树的部分知识就介绍到这里,因为高阶的数据结构并不适合用C语言来实现,所以数据结构还远远没有结束。