常见的几种最优化方法Matlab原理和深度分析
目录
生活或者工作中遇到各种各样的最优化问题，比如每个企业和个人都要
考虑的一个问题“在一定成本下，如何使利润最大化”等。最优化方法是一种数学方法，它是研究在给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优的一些学科的总称。随着学习的深入，博主越来越发现最优化方法的重要性，学习和工作中遇到的大多问题都可以建模成一种最优化模型进行求解，比如我们现在学习的机器学习算法，大部分的机器学习算法的本质都是建立优化模型，通过最优化方法对目标函数（或损失函数）进行优化，从而训练出最好的模型。常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度法等等。
1. 梯度下降法
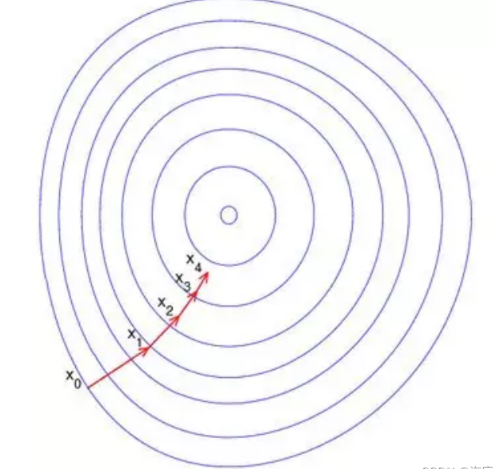
梯度下降法是最早最简单，也是最为常用的最优化方法。梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解。一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是”最速下降法“。最速下降法越接近目标值，步长越小，前进越慢。梯度下降法的搜
索迭代示意图如下图所示：
梯度下降法的缺点：
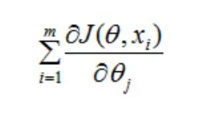
（1）靠近极小值时收敛速度减慢，如下图所示；
（2）直线搜索时可能会产生一些问题；
（3）可能会“之字形”地下降。
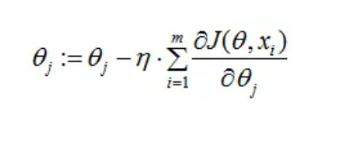
梯度下降法在接近最优解的区域收敛速度明显变慢，利用梯度下降法求解需要很多次的迭代。
在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法.
对一个线性回归（Linear Logistics）模型，假设下面的h(x)是要拟合的函数，J(theta)为损失函数，theta是参数，要迭代求解的值，theta求解出来了，那最终要拟合的函数h(theta)就出来了。其中m是训练集的样本个数，n是特征的个数。
1.1 批量梯度下降法（Batch Gradient Descent，BGD）
将J(theta)对theta求偏导，得到每个theta对应的的梯度：
由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta：