1. 线下评估策略
通常在数据竞赛中,参赛者是不能将全部数据都用于训练模型的,因为这会导致没有数据集对该模型的效果进行线下验证。为了解决这一问题,就要考虑如何对数据进行划分,构建合适的线下验证集。针对不同类型的问题,需要不同的线下验证方式,在此分为强时序性和弱时序性。
1.1 强时序性问题
对于含有明显时间序列因素的赛题,可将其看作强时间序行问题,即线上数据的时间都在离线数据集之后,这种情况下就可以采用时间上最接近测试集的数据做验证集
例如,天池平台上的“乘用车零售量预测”竞赛,初赛提供 2012 年 1 月至 2017 年 10 月车型销售数据,需要参赛者预测 2017 年 11 月的车型销售数据。这是一个很明显的含时间序列因素的问题,那么我们可以选择数据集的最后一个月作为验证集。
1.2 弱时序性问题
这类问题的验证方式主要为 K 折交叉验证,根据 K 的取值不同,会衍生出不同的交叉验证方式,具体如下。
- 当 K=2 时,这是最简单的 K 折交叉验证,即 2 折交叉验证。这个时候将数据集分成两份:D1 和 D2。首先,D1 当训练集,D2 当验证集;然后,D2当训练集,D1当验证集。2 折交叉验证存在很明显的弊端,即最终模型参数的选取将在极大程度上依赖于事先对训练集和验证集的划分方法。对于不同的划分方式,其结果浮动非常大。
- 当 K=N 时,也就是 N 折交叉验证,被称作 留一验证。具体做法是只留一个数据作为验证集,其他数据都作为数据集,并重复 N 次(N 为数据集总量)。其优点在于,首先它不受验证集和训练集划分方式的影响,因为每一个数据都单独做过验证集;其次,它用了 N-1 个数据训练模型,也几乎用到了所有数据,从而保证模型偏差更小。同时,其缺点在于计算量过大,如果数据集是千万级的,那么就需要训练千万次。
- 为了解决 1 和 2 中的缺陷,我们一般取 K=5 或 10,作为一种折中处理,这也是最常用的线下验证方式。
下面给出通用的交叉验证代码,具体代码如下:
from sklearn.model_selection import KFold
NFOLDS = 5
folds = KFold(n_splits=NFOLDS, shuffle=True, random_state=2021)
for trn_idx, val_idx in folds.split(X_train, y):
train_df, train_label = X_train.iloc[trn_idx, :], y[trn_idx]
valid_df, valid_label = X_train.iloc[val_idx, :], y[val_idx]
2. 评价指标
2.1 分类指标
(1)错误率与精度
在分类问题中,错误率是分类结果错误的样本数占样本总数的比例,精度则是分类结果中正确的样本总数的比例。
(2)准确率与召回率
假设一个肿瘤患病问题,患肿瘤的概率为0.5%,概率很小,对于这样一个一边概率远大于另一边的我们称为倾斜分类skewed class.
如果我们仍然采用accuracy来衡量这样的问题,那么对于一个始终预测y=0的模型,它预测上面的肿瘤问题的错误率也仅仅是0.5%.
Accuracy = (true positives + true negatives) / (total examples)
为此,我们引入Precision和Recall 如下所示:
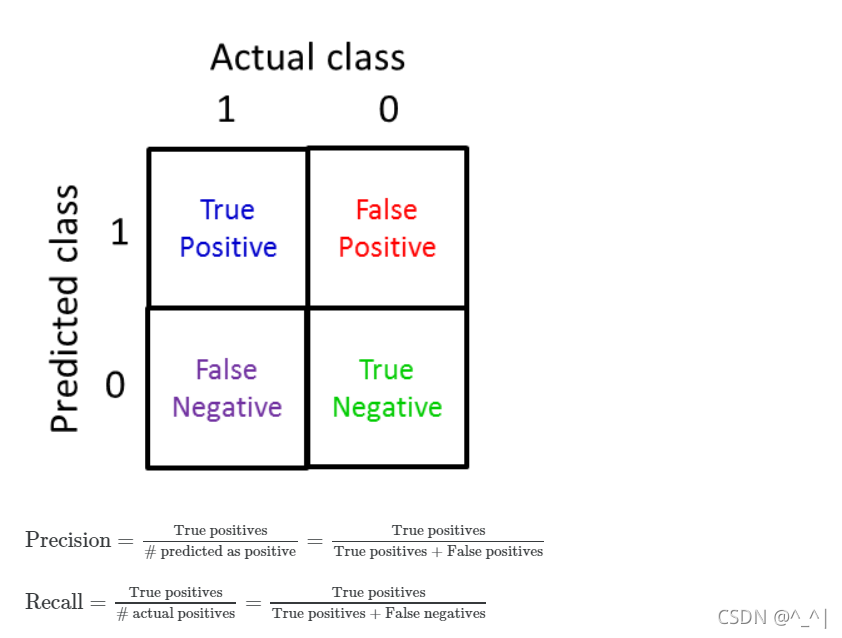
此时,如果我们用Precision和Recall去评判刚刚y=0的模型,那么结果都是0

一般而言,Precision和Recall的图像不固定,不过都呈现上图中的趋势。
当我们设高阈值时,我们得到的预测结果中得到肿瘤的概率也就越大因而Precision越高,不过可能漏掉一部分肿瘤的可能也越大从而Recall越高。
(3)F1-score
F1-score是权衡Precision和Recall后给出的一个评判模型的式子
F
1
=
P
R
P
+
R
F_1 = \frac{PR}{P+R}
F1=P+RPR
(4)ROC 曲线
ROC 曲线用于绘制采用不同分类阈值时的 TP 率(TPR)与 FP 率(FPR)。我们根据学习器的预测结果,把阈值从0变到最大,即刚开始是把每个样本作为正例进行预测,随着阈值的增大,学习器预测正样例数越来越少,直到最后没有一个样本是正样例。
TP率也叫真正例率,FP率也叫假正例率,注意区别于准确率和召回率。
T
P
R
=
T
P
T
P
+
F
N
TPR = \frac{TP}{TP+FN}
TPR=TP+FNTP
F
P
R
=
F
P
F
P
+
T
N
FPR = \frac{FP}{FP+TN}
FPR=FP+TNFP
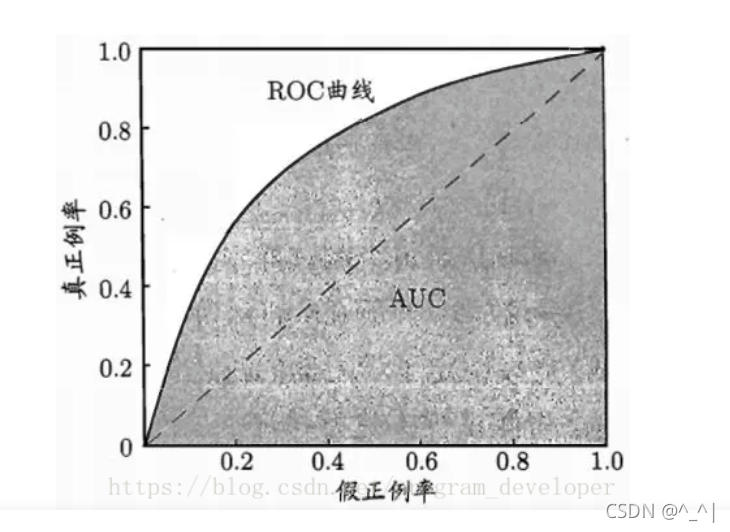
(5)AUC
AUC是一个极常用的评价指标,它定义为 ROC 曲线下的面积。之所以使用 AUC 作为评价指标,是因为ROC 曲线在很多时候并不嗯呢该清晰地说明哪个分类器的效果更好,而 AUC 作为一个数值,其值越大就代表分类器的效果越好。
(6)交叉熵
− ln L ( w , b ) = ∑ i n ∑ k m − y ^ k i ln f w , b ( x k i ) -\ln{L(w,b)} = \sum_{i}^{n}\sum_{k}^{m}-\hat{y}_k^i\ln{f_{w,b}(x^i_k)} −lnL(w,b)=i∑nk∑m−y^kilnfw,b(xki)
其在二分类问题上的表现形式为:
− ln ( w , b ) = ∑ i n − [ y ^ i ln f w , b ( x i ) + ( 1 − y ^ i ) ln ( 1 − f w , b ( x i ) ) ] -\ln{(w,b)} = \sum_{i}^{n}-[\hat{y}^{i}\ln{f_{w,b}(x^i)}+ (1-\hat{y}^{i})\ln{(1-f_{w,b}(x^i))}] −ln(w,b)=i∑n−[y^ilnfw,b(xi)+(1−y^i)ln(1−fw,b(xi))]
举个栗子,假设我们的一个sample经过softmax后得到的 y = f w , b ( x ) = [ 0.9 0.1 ] y=f_{w,b}(x)=\begin{bmatrix} 0.9 \\ 0.1\\ \end{bmatrix}\quad y=fw,b(x)=[0.90.1],其label为 y ^ = [ 1 0 ] \hat{y}=\begin{bmatrix} 1 \\ 0\\ \end{bmatrix}\quad y^=[10],那么在第一个式子里计算出的值为 − ( 1 ln 0.9 + 0 ln 0.1 ) = − ln 0.9 -(1 \ln0.9+0\ln{0.1})=-\ln0.9 −(1ln0.9+0ln0.1)=−ln0.9,第二计算结果即为 − ln 0.9 − 0 ln 0.1 -\ln0.9-0\ln0.1 −ln0.9−0ln0.1。再比方说,我们的另一个sample经过softmax后得到的 y = f w , b ( x ) = [ 0.1 0.8 0.1 ] y=f_{w,b}(x)=\begin{bmatrix} 0.1 \\ 0.8 \\ 0.1\\ \end{bmatrix}\quad y=fw,b(x)=⎣⎡0.10.80.1⎦⎤,其label为 y ^ = [ 0 1 0 ] \hat{y}=\begin{bmatrix} 0 \\ 1 \\ 0\\ \end{bmatrix}\quad y^=⎣⎡010⎦⎤,此时我们有 − ln L ( w , b ) = − 0 ln 0.1 − 1 ln 0.8 − 0 ln 0.1 = − ln 0.8 -\ln{L(w,b)}=-0\ln0.1-1\ln{0.8}-0\ln0.1=-\ln0.8 −lnL(w,b)=−0ln0.1−1ln0.8−0ln0.1=−ln0.8
像上面这样我们如果有两个distribution的点 y ^ \hat{y} y^和 y y y,我们记他们的交叉熵即为 H ( y ^ , y ) = − ∑ k y ^ k ln y k H(\hat{y},y)=-\sum\limits_{k}\hat{y}_k\ln{y_k} H(y^,y)=−k∑y^klnyk.
cross entropy交叉熵的含义是表达着两个distribution有多接近,如果这两个点的distribution一模一样的话,那它们计算出来的cross entropy就是0,用在我们这里的分类问题中,我们就是希望 y ^ \hat{y} y^与 y y y越接近越好。
2.2 回归指标
| 回归指标 | 计算公式 |
|---|---|
| MSE | 1 m ∑ i = 1 n ( y − y ^ ) 2 \frac{1}{m}\sum\limits_{i=1}^{n}(y - \hat{y})^2 m1i=1∑n(y−y^)2 |
| RMSE | 1 m ∑ i = 1 n ( y − y ^ ) 2 \sqrt{\frac{1}{m}\sum\limits_{i=1}^{n}(y - \hat{y})^2} m1i=1∑n(y−y^)2 |
3. 混淆矩阵和 heatmap
混淆矩阵
一图胜千言,其实就是对比实际和预测结果差异与关系的表格,之前讨论召回率时我们也有用过
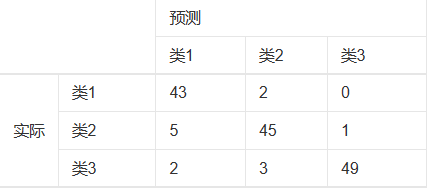
混淆矩阵可以帮助我们在分类问题中,用于分析模型对于那些样本或哪类样本预测能力不够从而导致结果不准确,然后分析造成结果误差的可能因素,最终修正训练数据和模型。
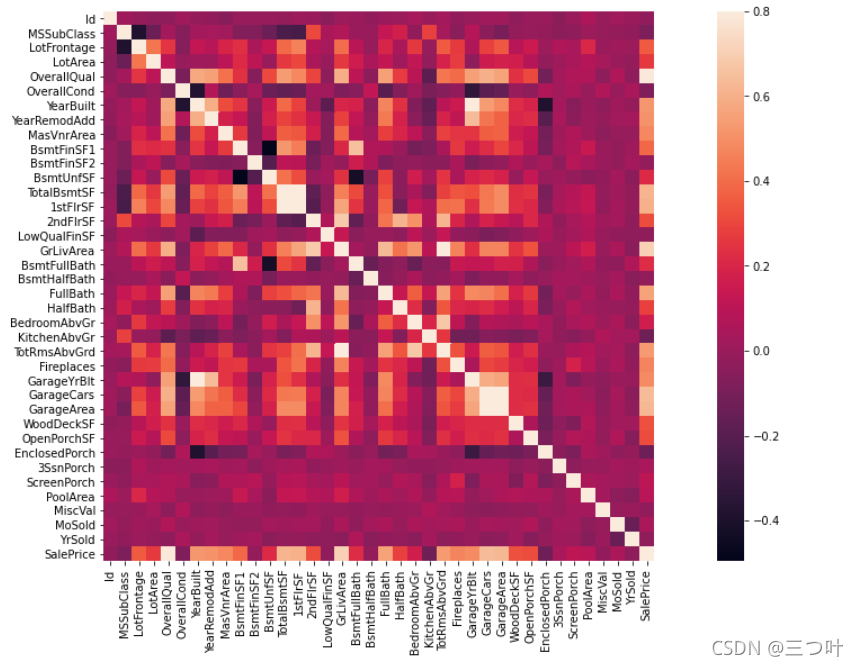
heatmap
热力图在实际中常用于展示一组变量的相关系数矩阵,在展示列联表的数据分布上也有较大的用途,通过热力图我们可以非常直观地感受到数值大小的差异状况。
其颜色可以直观地反映各变量之间的相关程度
import seaborn as sns
corrmat = train.corr() # 计算协方差矩阵,是 heatmap 的重要参数
f, ax = plt.subplots(figsize=(20,9))
sns.heatmap(corrmat, vmax=0.8, square=True)