选择排序,简单粗暴直观的排序算法。
一个长度为N的序列num[N],分为有序部分和无序部分
第一次,num[0]~num[N-1]是无序部分,从这N个数中选出最小的数,放在序列的第一个位置,
此时,num[0]是有序部分,num[1]~num[N]是无序部分
第二次,num[0]是有序部分,num[1]~num[N]是无序部分,从N-1个数中选出最小的数,放在序列的第二个位置,
此时,num[0]~num[1]是有序部分,num[2]~num[N]是无序部分
如此进行下去,整个序列最终为有序(顺序)序列
代码:
#include<stdio.h>
#define N 10
void selectsort(int *num , int length )
{
int i ;
int j;
int temp;//中间变量,供交换值的时候使用
for(i = 0;i < length ; i ++)//假设无序序列的第一个元素num[i]为最小值
{
for(j = i+1 ; j < length ;j++)//遍历最小值后面的所有元素(num[i+1]~num[length-1])
{
if(num[i] > num[j])//若找到比最小值num[i]还要小的元素,则与原来的最小值元素交换值
{
temp = num[i];
num[i] = num[j];
num[j] = temp;
}
}
}
}
int main()
{
int num[N] = {9,8,7,6,5,4,3,2,1,0};
selectsort(num , N);
for(int i=0; i < N;i++)
{
printf("%d ",num[i]);
}
printf("\n");
return 0;
}运行结果
看一下程序细节
时间复杂度
第一次需要遍历N-1个元素,第二次需要遍历N-2个元素······
所以时间复杂度是)O(N^2)
然而,细想一下,选择排序,每一趟遍历无序部分,却只为了找到那个最小的数,效率太低(老子辛辛苦苦在无序序列兜了一圈,只找一个最小值,这哪行,哪像计算机人搜搜扣扣的精神(又扣时间又扣空间))
于是,赶一只羊也是赶,赶两只羊也是赶。我们跑一趟无序序列,把最小值和最大值都找出来。
代码:
#include<stdio.h>
#define N 10
#include<time.h>
void swap(int *a,int *b)//函数作用,交换a和b的值
{
int temp ;
temp = *a;
*a = *b;
*b = temp;
}
void selectsort(int *num ,int n)
{
int start = 0;//无序部分的第一个元素
int end = N-1;//无序部分的最后一个元素
while(start < end)
{
int min_index = start;//最小值元素的下标
int max_index = end;//最大值元素的下标
int i = 0;
for(i = start;i<=end;i++)//遍历无序序列
{
if(num[i] < num[min_index])
min_index = i;//记录无序序列最小值元素的下标
if(num[i] > num[max_index])
max_index = i; //记录无序序列最大值元素的下标
}
swap(&num[start],&num[min_index]);//将找到的最小值放在序列开头
//错误语句实例 swap(&num[end],&num[max_index]);
//将找到的最大值放在序列末尾,看似合情合理,但在极端情况下与上一句语句是矛盾的
//本例就属于极端情况,此处挖一个坑
if(start == max_index)//极端情况,当最大值位于序列开头,要被最小值替换
{
max_index = min_index;
}
start++;//缩小无序序列长度,因为有序序列变长了
end--;
//细节演示
// for(int i = 0;i<N;i++)
// {
// printf("%d ",num[i]);
// }
// printf("\n");
}
}
int main()
{
int num[N] = {9,8,7,6,5,4,3,2,1,0};
selectsort(num,N);
for(int i = 0;i<N;i++)
{
printf("%d ",num[i]);
}
printf("\n");
return 0;
}运行结果:

程序细节:
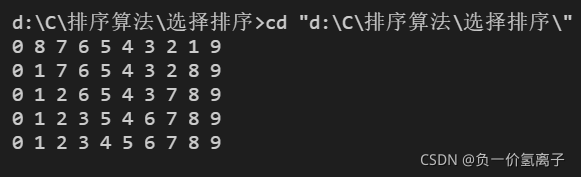
对比单向选择排序算法,双向选择排序虽然时间复杂都仍然是O(N^2),但是效率优化了50%左右
填坑:
我们需要排序的序列是num[10] = {9,8,7,6,5,4,3,2,1,0}
先来看一下错误代码

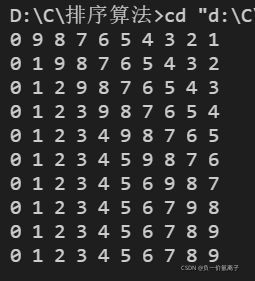
错误细节,每一次遍历序列的变化
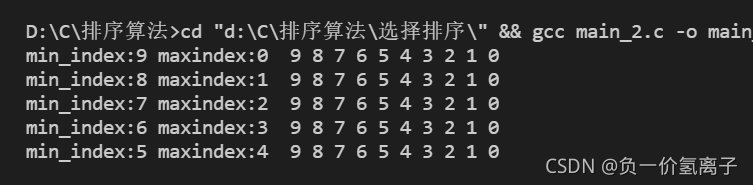
可以看到 ,第一次遍历,最小值下标是9,最大值下标是0,处理过程是将num[min_index]放在序列开头,num[max_index]放在序列末尾,即num[0] <——>num[9],即num[0]和num[9]只需要一次换值;
但是因为执行两次swap()(换值函数),相当于原来序列并没有发生变化
在以后的遍历中,也是这种情况,所以最终结果是序列没有任何变化,也就不难理解为何代码要做如下处理
正确代码

正确细节,每一次遍历序列的变化