区块链系统包含了计算机科学过去几十年的成果:计算机网络P2P、算法、数据库、分布式系统、计算机密码学等
密码学是区块链系统安全性保障的基础技术,形象地称为区块链的骨骼
哈希算法
■哈希算法(Hash、 散列、杂凑, 消息摘要, 音译为哈希,原意是古法语“斧子”, 后引申为“剁碎的肉末”)
■哈希算法:把任意长度的输入做复杂的变换后,输出固定长度的输出,这个输出称为输入的哈希值而相应的变换方法称为哈希算法,在不引起混淆的情况下,哈希算法也称哈希函数
■哈希算法的输出长度和输入长度无关
■哈希这种转换是一种压缩映射 ,即散列值的空间通常远小于输入的空间
■哈希算法的输入可以是字符串,可以是数据,可以是任何文件
■作用:可以求/作为信息输入的摘要,或者指纹
■当需要比较两条消息是否一 致时, 通过对比“指纹”就能知道两条消息是否一致
对于n比特长的哈希函数,找到碰撞的计算复杂度为2^n/2
二、对称加密和非对称加密
1. 对称加密
对称加密指的就是加密和解密使用同一个秘钥,所以叫做对称加密。对称加密只有一个秘钥,作为私钥。
常见的对称加密算法:DES,AES,3DES等等。
2. 非对称加密
非对称加密指的是:加密和解密使用不同的秘钥,一把作为公开的公钥,另一把作为私钥。公钥加密的信息,只有私钥才能解密。私钥加密的信息,只有公钥才能解密。
常见的非对称加密算法:RSA,ECC
理解:
你可以用你的私钥加密一封信,所有人都可以用你的公钥解开来看,这可以确保这是你写的
所有人都可以用你的公钥加密写信给你,只有你自己使用你的私钥解密可以查看
公钥密码算法——陷门函数/活门函数/单向函数
非对称加密算法最关键的是它们都有自己独特的陷门函数
陷门函数是一种只能单向计算,至少是在一个方向上易于计算的函数(如果使用现代计算机从一个方向暴力破解,需要数百万xx年时间)
非陷门函数的例子:
A+B=C
已知A,B就可以算出C,但是同样,知道B,C也可以很容易得到A
陷门函数:
“i love u”+public key = "absd12394704su"
已知“i love u”和公钥,可以算出“absd12394704su”
但是知道“absd12394704su”和公钥,无法知道得出“i love u”
RSA算法:
RSA算法在已提出的公开密钥算法中,最为流行, 也最容易理解和实现的一个sua
RSA用于保密性时 ,就是公钥加密 ,私钥解密。 因为公钥是可以公开 ,任何人都可以使用公钥对信息进行加密,但是只有持有私钥的人才能正确解密。这样就保证了信息的保密性,因为只有私钥持有者才能正确解密。
RSA用于认证性时 ,比如数字签名 ,即私钥持有者对信息进行签名 ,验证者可以根据公开的公钥进行验证签名是否正确和有效。即实现了认证性,以及不可抵赖性。
公钥密码的分类:
公钥密码算法基于计算复杂度上的难题,(不可计数的实现),通常来自于数论,主要依赖于两类数学难题:
大整数因子分解问题(IFP问题):属于NP类是否存在多项式时间算法是受学者关注的
离散对数问题(简称DLP问题)
椭圆曲线加密算法
参考博客:
ECC椭圆曲线加解密原理详解(配图)_Mark的博客-CSDN博客_ecc加密
RSA的解决分解整数问题需要亚指数时间复杂度的算法,而目前已知计算椭圆曲线离散对数问题(ECDLP)的最好方法都需要全指数时间复杂度。这意味着在椭圆曲线系统中我们只需要使用相对于RSA 短得多的密钥就可以达到与其相同的安全强度。例如,一般认为160比特的椭圆曲线密钥提供的安全强度与1024比特RSA密钥相当。使用短的密钥的好处在于加解密速度快、节省能源、节省带宽、存储空间。
比特币以及中国的二代身份证都使用了256 比特的椭圆曲线密码算法。
威尔斯特拉斯方程:
椭圆曲线的椭圆一词来源于椭圆周长积分公式。(这个命名深究起来比较复杂,了解一下就可以了),一条椭圆曲线是在射影平面上满足威尔斯特拉斯方程(Weierstrass)所有点的集合。
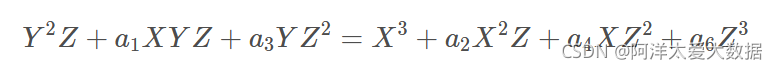
对普通平面上点(x,y),令x=X/Z,y=Y/Z,Z≠0,得到如下方程:
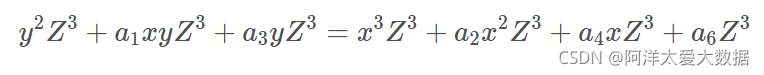
简化版的Weierstrass方程:
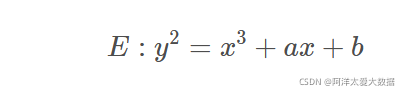
其中,
非椭圆曲线示例:

椭圆曲线阿贝尔群
我们已经看到了椭圆曲线的图象,但点与点之间好象没有什么联系。我们能不能建立一个类似于在实数轴上加法的运算法则呢?这就要定义椭圆曲线的加法群,这里需要用到近世代数中的阿贝尔群。
在数学中,群是一种代数结构,由一个集合以及一个二元运算所组成。已知集合和运算(G,*)如果是群则必须满足如下要求。
封闭性: ∀a,b∈G,ab ∈ G
结合性: ∀a,b,c∈G ,有 (ab)c = a (b*c)
单位元: ョe∈G, ∀a ∈G,有ea = ae = a
逆元: ∀a ∈G ,ョb∈G 使得 ab = ba = e
交换性: ∀a,b∈G,ab = ba
同样在椭圆曲线也可以定义阿贝尔群。
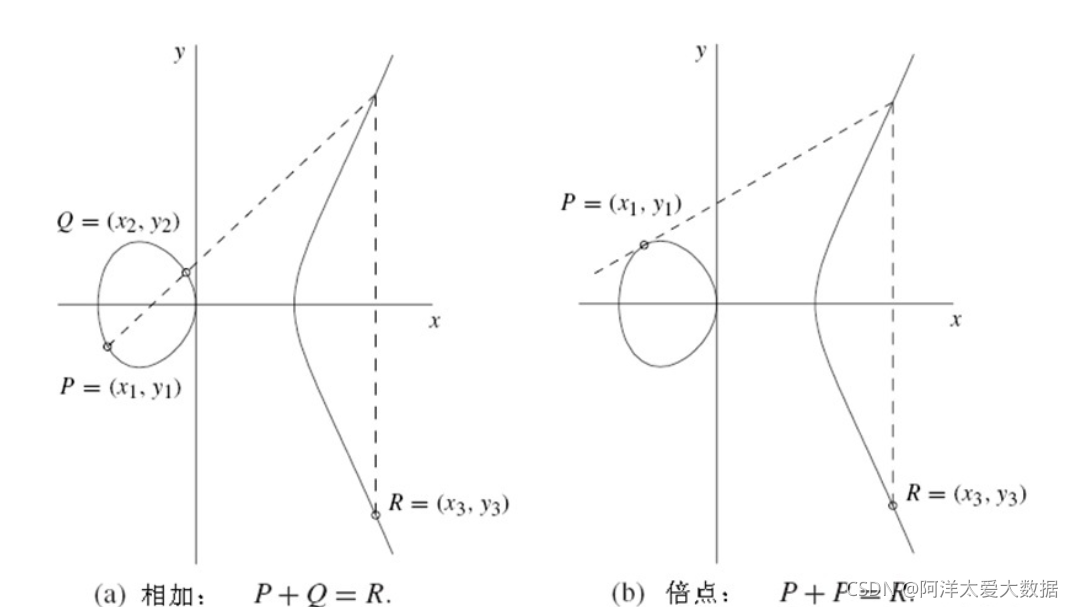
任意取椭圆曲线上两点P、Q(若P、Q两点重合,则作P点的切线),作直线交于椭圆曲线的另一点R’,过R’做y轴的平行线交于R,定义P+Q=R。这样,加法的和也在椭圆曲线上,并同样具备加法的交换律、结合律。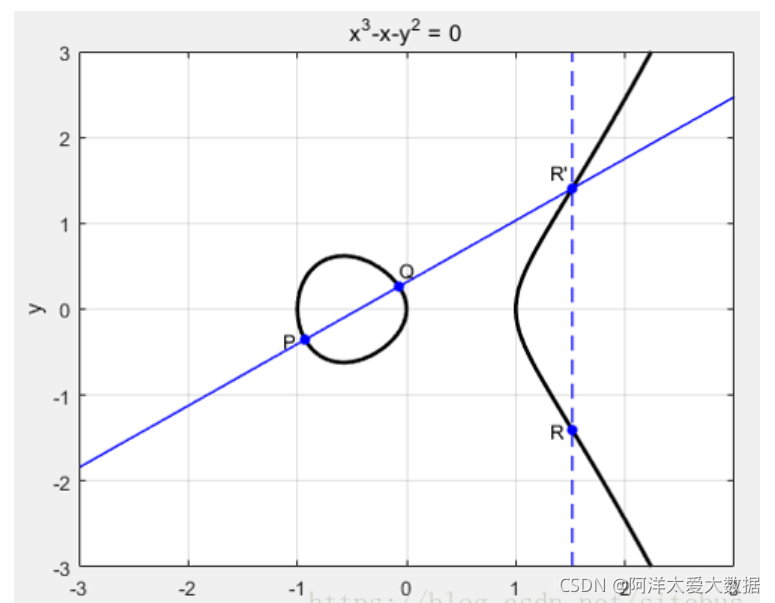
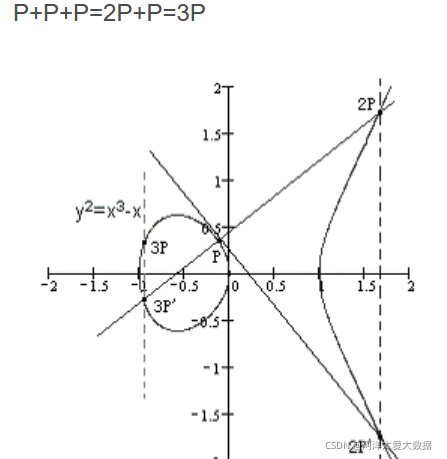
同点加法
若有k个相同的点P相加,记作kP 。 P+P=2
椭圆曲线加密
考虑 K = k G K=kG K=kG ,其中K、G为椭圆曲线Ep(a,b)上的点,n为G的阶( n G = O ∞ nG=O_∞ nG=O∞ ),k为小于n的整数。则给定k和G,根据加法法则,计算K很容易但反过来,给定K和G,求k就非常困难。因为实际使用中的ECC原则上把p取得相当大,n也相当大,要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据 。
点G称为基点(base point)
k ( k < n ) k(k<n) k(k<n)为私有密钥(private key)
K为公开密钥(public key)

3. 区别
对称加密算法相比非对称加密算法来说,加解密的效率要高得多。但是缺陷在于对于秘钥的管理上,以及在非安全信道中通讯时,密钥交换的安全性不能保障。所以在实际的网络环境中,会将两者混合使用.
| 需求 | 描述 |
| 输入长度可变 | H可应用于任意大小的数据块 |
| 输出长度固定 | H产生定长的输出 |
| 效率 | 对于任意给定的x,计算H(x)比较容易 |
| 抗原像攻击(单向性) | 对任意给定的hash码h,找到满足H(y)=h 在计算上是不可行的 |
| 抗第二原像攻击(抗强碰撞性) | 对任何给定的分块x,找到满足y≠x且H(x) =H(y) 的y在计算上是不可行的 |
| 抗碰撞攻击(抗强碰撞性) | 找到任何满足H(x) = H(y)的偶对 (x,y)在计算上是不可能的 |
| 伪随机性 | H的输出满足伪随机性测试标准 |
弱Hash函数:只满足以上前五个要求的Hash函数
强Hash函数:满足以上前6个要求的Hash函数