原文标题: Selfish Mining Attacks Exacerbated by Elastic Hash Supply
原文作者: Yoko Shibuya, Go Yamamoto, Fuhito Kojima, Elaine Shi ,Shin’ichiro Matsuo, and Aron Laszka
原文机构: NTT Research, Cornell University, Georgetown University, University of Houston
原文地址: https://fc21.ifca.ai/papers/233.pdf
发表日期/期刊: 2021/Financial Cryptography and Data Security
笔记整理: doxbwx@163.com
一、简介
之前的工作已经提出了许多攻击,即使没有达到总算力的50%也可以对区块链攻击并获取利益。例如selfish mining 以及 block withholding等。实际过程中,矿工都是以利润为导向,而之前工作的大多数模型的假设链都是固定的。都没有考虑诚实的矿工在发生攻击时如何对盈利能力的变化做出反应。
- 本文使用真实世界的数据记录并且对这些数据进行分析,
- 表明挖矿的盈利能力与总哈希率之间存在统计上的显著相关性。
- 证实矿工确实对不断变化的盈利能力做出了反应。
- 提出一个具有弹性算力供应的模型。 在这个模型下,自私挖矿要么导致链崩溃,要么就保持稳定。
对selfish mining详细过程感兴趣可以看这里
https://blog.csdn.net/qq_41084082/article/details/121451961?spm=1001.2014.3001.5501
二、对“仓促”自私矿工的分析
假设全网总算力为1,挖一个块的成本为1,挖到一个块的收益为1,有α∈(0,1)比例的算力串通自私矿工,剩下的1-α是诚实的矿工。
因为自私矿工的攻击可以抵消诚实矿工挖到的块,这就提高了矿工的挖矿成本,这也就导致诚实的矿工很容易亏钱,所以就有一部分会离开。这里我们假设离开了β部分的矿工,则剩下的就是1-α-β
- 当α > 1 - α - β时,这时候自私矿工所在的私有分支的算力就高于公有分支,私有分支会公开成为主链,则所有的诚实矿工都没有了收益,都会选择离开,这就导致了系统崩溃
- 当α < 1 - α - β时,公有分支上的算力变成了1 - α - β,挖一个块的成本也就变成了1 - α - β,而α算力会被自私矿工抵消,所以只有(1 - α - β - α)/(1 - α - β )的部分才能得到报酬。总的利润=收益-成本=
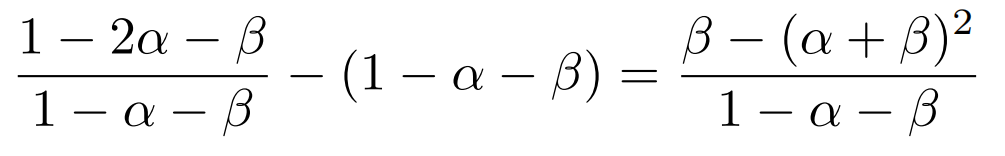
- 当α = 1 - α - β时,剩下的算力全部被自私矿工抵消,则收益为0。从上述公式可以看出一些结论
- 制度崩溃
如果α>1/4,则无论β是多少,总利润一定小于0,这样诚实的玩家都会亏钱,所以制度会崩溃。 - 一些诚实的算力还在
如果α <= 1/4,一些算力还是存在,系统会进入一个新平衡。当α=1/4时,β=1/4才会达到新的平衡,这时总算力=1/2,所以挖出一个块的成本为1/2。然而剩余诚实算力的一半被自私矿工抵消,所以这种情况收支平衡。
无论哪种情况,由于弹性哈希力的存在,自私挖掘带来的不公平加剧了。
三、实证研究
数据:
| 数据类型 | 来源 | 时间 |
|---|---|---|
| 比特币数据 | Quandl | 2015/1/1 - 2020/7/31 |
| 以太坊数据 | Etherscan | 2017/1/1 - 2020/7/31 |
| 以太坊经典数据 | BigQuery | 2017/1/1 - 2020/7/31 |
消除时间趋势方法
想观察矿工收入变化时,总算力的变化。如果不消除时间序列数据的趋势,则相关性会变高。
使用宏观经济学中的time-detrending过滤器(Hodrick-Prescott (HP)、Baxter-King (BK) 和 Christiano-Fitzgerald (CF)),可以将缓慢移动的趋势成分与较短范围的周期性分开。
文章中,对总哈希率和矿工收入的时间序列数据中应用了HP过滤器。

回归方程: 估计总哈希率相对于每哈希收入的弹性。回归方程如下所示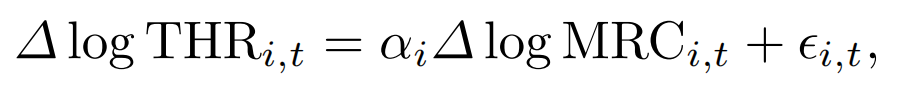
THR 代表总哈希率,
MRC 代表矿工从 coinbase 获得的每个哈希收入。
参数 i 是代表加密货币(比特币、以太坊或以太坊经典)的索引,
t 是时间(天)的索引。
带有 ∆ 的变量是记录变量的周期分量。
在回归中包含年月固定效应,以去除一些年/月固定事件,时间去趋势过滤器可能无法去除这些事件。
3.2 结果
表一表明,总哈希率相对于矿工从 coinbase 获得的每个哈希收入而言是有弹性的。矿工从 coinbase 获得的每个哈希收入的 1 个百分比变化会导致总哈希率发生 0.027 到 0.183 个百分比的变化。
表二表明,随着货币的增长,哈希率可能对矿工的收入更加敏感。


四、具有弹性哈希供应的模型
该模型中,平衡状态由两个相反的影响决定。 攻击增加了诚实矿工的挖矿成本,从而使诚实矿工离开。 同时,当一些诚实的矿工离开时,总算力下降,诚实矿工的挖矿成本也随之下降。
这两种状态都由攻击者的初始算力份额有关,所以得出攻击者的初始份额阈值。
- 攻击者的份额低于阈值,则系统具有稳定的平衡,由诚实的矿工提供正哈希值;
- 如果攻击者的份额高于阈值,所有诚实的矿工都离开,系统崩溃。
两种情况都会有诚实的矿工离开,在弹性哈希供应下,自私挖矿的影响会显著加剧。
| 符号 | 意义 |
|---|---|
| B | 新区块的预期奖励,包括 coinbase 和交易费用 |
| C | 某个矿工找到一个新块之前,每单位哈希率的预期挖掘成本 |
| H | 诚实矿工的总算力 |
| M | 攻击池的哈希率 |
没有自私挖掘的基线模型: 一群诚实矿工和一个攻击池组成的系统。
矿工均衡算力(H*):使得诚实矿工在算力H* 下获得0利润
假设M、B、C时固定的,且满足M < B/C。
在没有自私挖矿的情况下,诚实矿工单位算力的利润为UN(H) = 收益 - 成本 = B(1/(H+M)) - C。
在均衡中,弹性哈希供应假设意味着UN(H*) = 0。我们可以求解H* = B/C - M > 0。
带有自私挖矿的模型:
进攻池和诚实矿工预期挖矿奖励Battacker和Bhonest
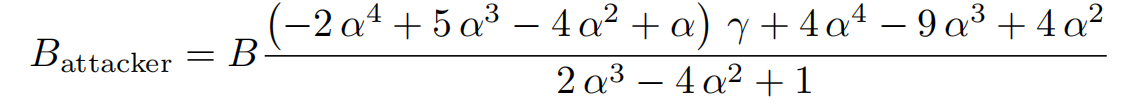
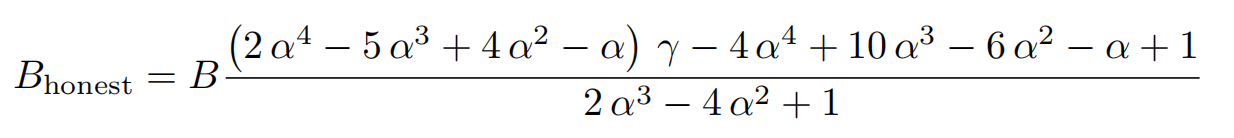
α = (M/(H+M)) 攻击池的算力占总算力的比例
γ 表示攻击池上的诚实矿工比例
总有效算力为(Battacker + Bhonest)(H+M)/B
诚实矿工算力Bhonest(H+M)/B = H·Bhonest/((1-α)B)
攻击池算力Battacker(H+M)/B = M· Battacker/αB
则诚实矿工在自私挖矿攻击下每算力的利润为

在均衡中,诚实矿工的哈希供应量
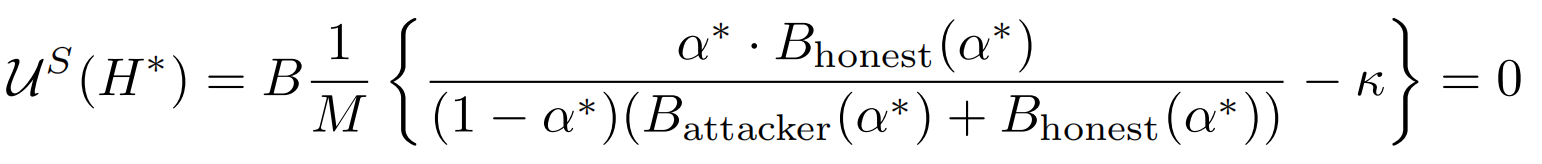
其中,α* = M/(H*+M) , k = M · C/B
攻击者初始份额H* >阈值M。如果没有,那么系统无法找到诚实矿工在自私挖矿攻击下留在系统中的均衡。 下面简单的定理回答了攻击者的哈希率必须有界以避免系统崩溃。
定理1. 对于任何给定的 γ,存在Mmax ,使得 US (H*) = 0 且 H*> M(> 0) 的解 存在当且仅当 M ≤ Mmax。
五、结论
大多数自私的挖矿文献都假设总哈希能力是固定的。 我们的结果表明,弹性哈希供应可以显着加剧自私挖矿的影响。
- 凭经验表明,相对于矿工的每个哈希收入而言,哈希供应是有弹性的,
- 理论上推导出了一个阈值,如果攻击者在总算力中的初始份额高于阈值,则所有诚实的矿工 将离开,链条崩溃
作者理论分析不够全面,未来可能会对这方面进行补全。
- 能否达到平衡取决于起始状态。H=0时,哈希算力<M时,任何诚实的个体矿工开始挖矿都将无利可图
- 分析忽略了瞬态效应,这可能会阻止达到特定的平衡。如果难度调整被延迟,M ≤ f(αmax ) B/C的攻击者可能能够在难度调整以激励他们留下来之前“赶走”诚实的矿工。