剑指 Offer 64. 求1+2+…+n - 力扣(LeetCode) (leetcode-cn.com)
https://leetcode-cn.com/problems/qiu-12n-lcof/submissions/
求1~n的连加之和
求n的连加之和,有以下思路
1,常规思路
int sum = 0; int i = 1; for(i = 1;i <= n;i++) sum += i; return sum;使用for循环完成连加操作
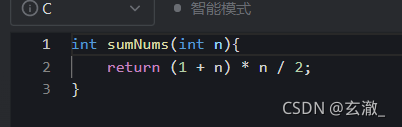
2,公式法
int sumNums(int n){ return (1 + n) * n / 2; }使用前n项和的求和公式 n * (n + 1) / 2;
3,递归方法
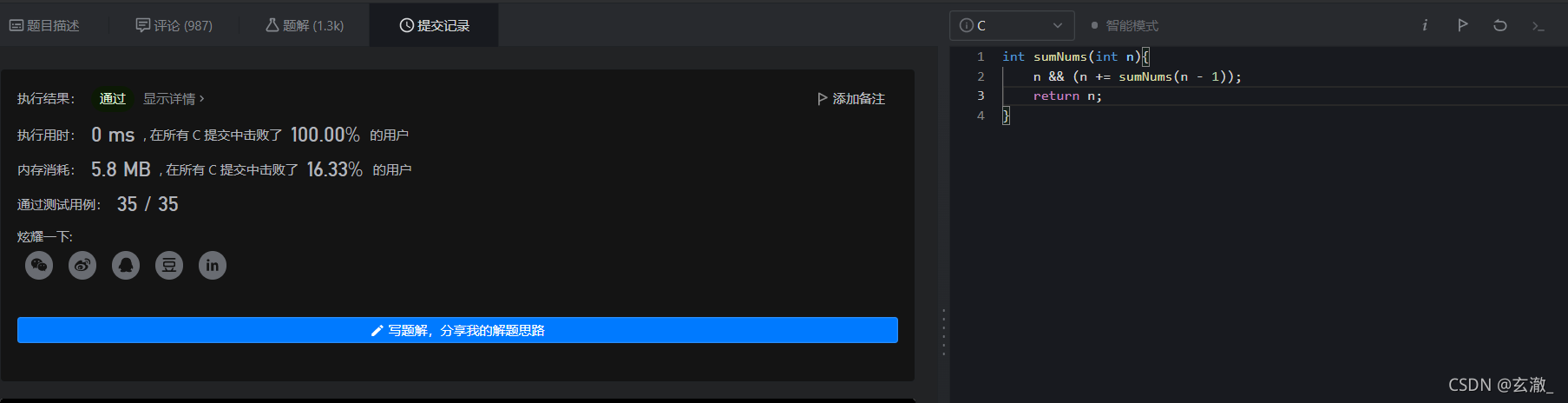
以逻辑运算符&&为例,对于 A && B这个表达式,如果A的返回值为 False ,此时不会去执行表达式B。
利用这个特性,我们可以将判断是否为递归的出口看做 A && B 中的 A 部分,递归的主体函数看成是 B 部分。如果不是递归出口,则返回 True ,并继续执行表达式的 B部分,否则递归结束。
int sumNums(int n){ n && (n += sumNums(n - 1)); return n; }
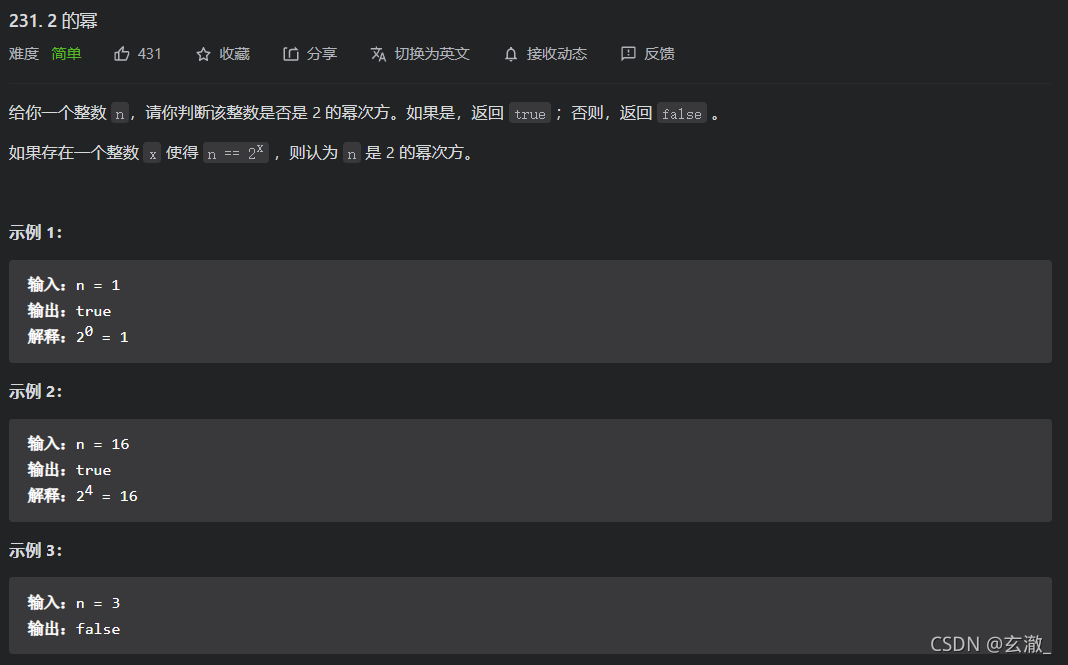
231. 2 的幂 - 力扣(LeetCode) (leetcode-cn.com)
方法一,穷举法
使用for循环进行判断
bool isPowerOfTwo(int n){ int i; unsigned int k = 1; if(n < 0) return false; if(n == 1) return true; for(i = 1;i <= 31;i++) { k *= 2; if(k == n) return true; } return false; }方法二
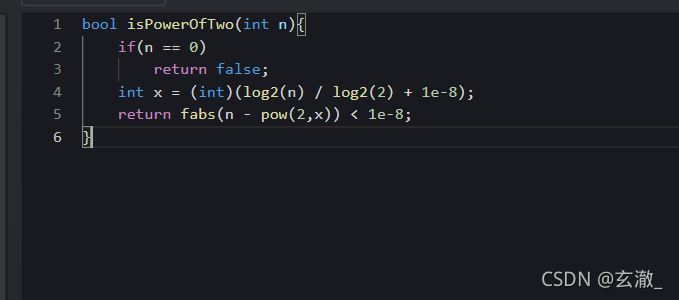
bool isPowerOfTwo(int n){ if(n == 0) return false; int x = (int)(log2(n) / log2(2) + 1e-8); return fabs(n - pow(2,x)) < 1e-8; }将原式进行对数运算,得到如上结果,进行浮点数判断
方法三,二进制表示
一个数n是2的幂,当且仅当n是正整数,并且n的二进制表示中仅含一个1
我们可以考虑使用位运算,将n的二进制中表示最低位的那个1提取出来,再判断剩下的数是否为0即可
(1),n & (n - 1)== 0
(2),n & ( -n ) == n
bool isPowerOfTwo(int n){ return n > 0 && (n & (n - 1)) == 0; }
231. 2 的幂 - 力扣(LeetCode) (leetcode-cn.com)
方法一
类比上面的二次幂,可以使用穷举法
方法二
对原式进行数学运算,然后进行浮点数精度判断
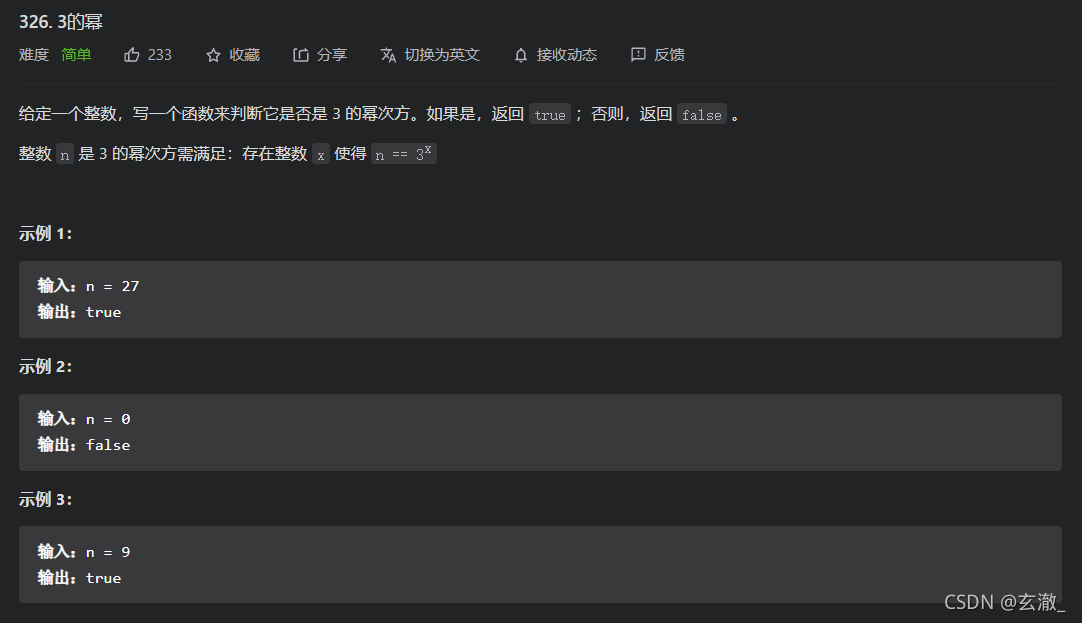
bool isPowerOfThree(int n){ if(n == 0) return false; int x = (int)(log(n) / log(3) + 1e-8); return fabs(n - pow(3,x)) < 1e-8; }342. 4的幂 - 力扣(LeetCode) (leetcode-cn.com)
1492. n 的第 k 个因子 - 力扣(LeetCode) (leetcode-cn.com)
方法一,枚举法
int kthFactor(int n, int k){ int i = 0; for(i = 1;i <= n;i++) { if(n % i == 0) k--; if(k == 0) return i; } return -1; }
367. 有效的完全平方数 - 力扣(LeetCode) (leetcode-cn.com)
方法一,使用函数进行判断
#include <math.h> bool isPerfectSquare(int num){ if(sqrt(num) == (int)sqrt(num)) return true; return false; }方法二:暴力枚举
bool isPerfectSquare(int num){ long x = 1,square = 1; while(square <= num) { if(square == num) return true; ++x; square = x * x; } return false; }