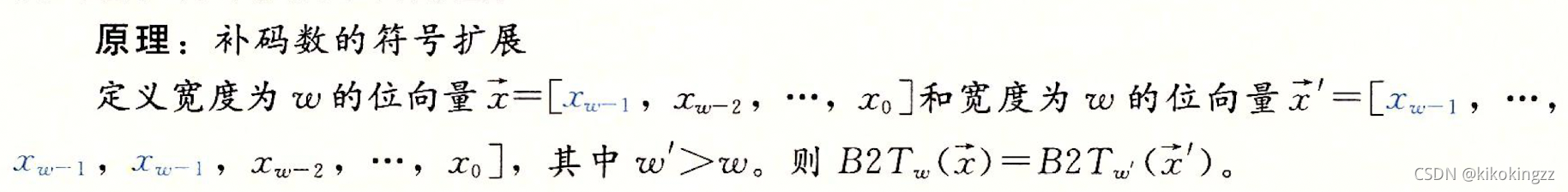🌕写在前面
- 🍊博客主页:kikoking的江湖背景
- 🎉欢迎关注🔎点赞👍收藏⭐️留言📝
- 🌟本文由 kikokingzz 原创,CSDN首发!
- 📆首发时间:🌹2021年11月25日🌹
- 🆕最新更新时间:🎄2021年11月25日🎄
- ✉️坚持和努力一定能换来诗与远方!
- 🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢感谢感谢!
本系列为拓展专题,文章都不会太长,但是都对日后的编程学习有很大帮助
或许会给你提供一个新的解题思路也不一定哦!欢迎订阅本专栏,每周更新!

目录
🌕写在前面
🦸♂️:题目1.你能在5秒内写出 -6 的32位补码吗?
🦸♂️:题目2.你能3秒说出这个32位的补码对应的十进制值是多少吗?
❗️常规计算模式如下
✅修炼第一步
✅考前抱佛脚
⭕️终极面试
🍊ps:计算机中对于有符号数存储的是补码形式!
你进入考场,面试官对面微微一笑:
🦸♂️:题目1.你能在5秒内写出 -6 的32位补码吗?
🦸♂️:题目2.你能3秒说出这个32位的补码对应的十进制值是多少吗?
11111111 11111111 11111111 11111101
🧑💻:如果你在脑海里还在想着原码、反码和补码转换,那只能说5秒真的不够用
🧑💻:但如果你掌握了下面的方法,3秒足以!
✨✨✨我是分割线✨✨✨
❗️常规计算模式如下
整数有3种二进制表示形式
1.原码
2.反码
3.补码
正整数——原码、反码、补码相同
int a =5; //a是正数 a 是整型,a占4个字节——>32位 00000000 00000000 00000000 00000101 —— 原码 00000000 00000000 00000000 00000101 —— 反码 00000000 00000000 00000000 00000101 —— 补码负整数——原码、反码、补码不同要进行计算
✨✨✨我是分割线✨✨✨
✅修炼第一步
想要快速写出补码,我们首先要了解 将补码转换为十进制的转换方式
可见,补码的最高位位权为负,其余计算方式同二进制转十进制相同,于是我们如果能够熟练记忆二进制的位权,那么补码是不是就可以随手写了呢?
对!我们看这道小题
✨✨✨我是分割线✨✨✨
✅考前抱佛脚
单单仅依靠补码编码的定义可以5秒内写出补码,但是32位的补码该如何写出呢?这里我们还需要知道 补码数的符号扩展:
·3位补码[101]表示值-4+1= -3;对它应用符号扩展,得到4为补码[1101], 表示的值 -8+4+1=-3;我们可以看到, 对于[1101], 最高两位的组合值是 -8+4=-4, 与[101]时符号位的值相同;类似地,位向量[111]和[1111]都表示值一1
我们不难发现,只要在补码的左边补上原补码的最高位的数字(1或0,这里是1),那么无论扩充到多少位,补码的值始终不变!
[11] = -2 + 1 = -1
[111] = -4 + 2 + 1 =-1
[1111] = -8 + 4 + 2 + 1 = -1
[11111] = -16 + 8 +4 + 2 + 1 =-1
✨✨✨我是分割线✨✨✨
⭕️终极面试
考官出题1:同学,你能在5秒内写出-6的补码吗,要求是32位的哦补码哦!
应用---->补码数的符号扩展
回答正确!
考官出题2:你能3秒说出这个32位的补码对应的十进制值是多少吗?
11111111 11111111 11111111 11111101
解:kikoking想法如下:
由补码数符号扩展的逆运算可得 上面的32位补码的实质是3位补码[101]扩展到32位
也就是 -4 +1 =-3
回答正确!
✨✨✨我是分割线✨✨✨
🍊ps:计算机中对于有符号数存储的是补码形式!
11111111 11111111 11111111 11111011 —— -5的补码 f f f f f f f b VS编译器在内存窗口是16进制的 即 0xfffffffb小端法显示: