一、实验目的
完整代码链接 :完整代码链接
- 掌握二叉树的定义和性质。
- 理解二叉树的各种存储结构的表示方法。
- 掌握二叉树的先序、中序、后序及按层遍历方法和相应算法。
- 掌握二叉树的其他基本操作,体会算法的递归性。
二、预备知识 - 阅读课程教材P121~125页内容,理解二叉树的逻辑定义,掌握其重要性质。
- 阅读课程教材P126~131页内容,熟悉二叉树的存储结构,掌握二叉链表存储结构下二叉树各种遍历方式及其它操作的实现算法,体会递归算法的设计思路。
- 体会二叉树的按层遍历算法中队列的应用。
············三、实验内容
按如下要求编写程序,进行调试,写出调试正确的源代码,给出测试结果。
在二叉链表存储结构下,实现如下操作:
1.使用递归方法创建一个非空二叉树T。
2.对二叉树T进行先序、中序、后序及按层遍历,并输出遍历结果。
3. 统计并输出该二叉树中叶子结点的数目。
4. 交换该二叉树的左右子树,并对其重新进行遍历,输出遍历结果。
5. 计算并输出该二叉树的深度。
说明:
(1)二叉树的初始形态自定。
(2)二叉树的按层遍历算法中运用了抽象数据类型队列,其存储表示与实现方法自定(可以是链队列,也可以是循环队列)。
准备工作
1.创建二叉树结构体
2.构建一个循环队
//创建二叉树结构体;
typedef struct BiTNode {
int data;
struct BiTNode *lchild, *rchild;//左右孩子指针
}BiTNode, *BiTree;
//构建一个循环队列
typedef struct Qnode {
BiTNode *base;
int front;//头
int rear;//尾
}sqQueue;
定义一个类
class tree {
private:
BiTree root;
sqQueue q;
public:
tree() {//构造函数
CreatBiTree(root);
}
BiTree get_root() {//得到root节点;
return root;
}
//创建一个循环队列
void InitQueue(sqQueue &q)
//创建二叉树
BiTree CreatBiTree(BiTree &t
//先序遍历
void PreOrderTraverse(BiTree &t)
//中序排序
void InOrderTraverse(BiTree &t)
//后序遍历
void PostOrderTraverse(BiTree &t)
//层序遍历
void LevelOrderTraverse(BiTree &t
//统计节点的数目
void Count_TreeEnds(BiTree &t, int &n
//交换左右子树
BiTree Exchange(BiTree &t
//5. 计算并输出该二叉树的深度。
int Depth(BiTree &t
};
类成员函数详细说明(代码)
一些基础成员函数说明:
//构造函数
tree() {
CreatBiTree(root);//调用创建二叉树函数
}
BiTree get_root() {//得到root节点;
return root;
}
/****************************************/
//创建一个循环队列
void InitQueue(sqQueue &q) {
q.base = new BiTNode[5];
q.front = q.rear = 0;
}
1.创建二叉树
BiTree CreatBiTree(BiTree &t) {
int val;
cin >> val;
getchar();
if (val <= 0) t = NULL;
else {
t = new BiTNode;
t->data = val;
CreatBiTree(t->lchild);
CreatBiTree(t->rchild);
}
return t;
}
2.先序遍历
void PreOrderTraverse(BiTree &t) {
if (!t) return;
else {
cout << t->data << " ";
PreOrderTraverse(t->lchild);
PreOrderTraverse(t->rchild);
}
}
3.中序排序
//中序排序
void InOrderTraverse(BiTree &t) {
if (!t) return;
else {
InOrderTraverse(t->lchild);
cout << t->data << " ";
InOrderTraverse(t->rchild);
}
}
4.后序遍历
//后序遍历
void PostOrderTraverse(BiTree &t) {
if (!t) return;
else {
PostOrderTraverse(t->lchild);
PostOrderTraverse(t->rchild);
cout << t->data << " ";
}
}
5.层序遍
队列实现:
仔细看看层序遍历过程,其实就是从上到下,从左到右依次将每个数放入到队列中,然后按顺序依次打印就是想要的结果
实现过程
1、首先将二叉树的根节点入队,判断队列不为NULL,就输出队头的元素,
2、判断当前节点如果有孩子,就先入队左孩子 然后入队右孩子
3、遍历过的节点出队列,
4、循环以上操作,直到 队列= NULL。
//层序遍历
void LevelOrderTraverse(BiTree &t) {
if (!t)return;
else {
InitQueue(q);//调用前面的创建队列函数
q.base[q.rear] = *t;
q.rear = (q.rear + 1) % 5;//循环队列队尾改变
}
while (q.front != q.rear) {
BiTNode temp = q.base[q.front];
cout << temp.data << " ";
if (temp.lchild) { //入队左孩子
q.base[q.rear] = *temp.lchild;
q.rear = (q.rear + 1) % 5;//循环队列队尾改变
}
if (temp.rchild) {//入队右孩子
q.base[q.rear] = *temp.rchild;
q.rear = (q.rear + 1) % 5;//循环队列队尾改变
}
q.front = (q.front + 1) % 5;//对头改变
}
}
6. 统计节点的数目
7.交换左右子树
8.计算并输出该二叉树的深度
//统计节点的数目
void Count_TreeEnds(BiTree &t, int &n) {
if (t) {
if (!t->lchild && !t->rchild)//叶子结点没有左右孩子
n++;
Count_TreeEnds(t->lchild, n);//不是叶子结点就递归调用
Count_TreeEnds(t->rchild, n);
}
}
//交换左右子树
BiTree Exchange(BiTree &t) {
if (!t)return NULL;
BiTree lchild = Exchange(t->rchild);
BiTree rchild = Exchange(t->lchild);
t->lchild = lchild;
t->rchild = rchild;
return t;
}
// 计算并输出该二叉树的深度。
int Depth(BiTree &t) {
int l = 0, r = 0
if (t == NULL) return 0;
l = Depth(t->lchild) + 1;
r = Depth(t->rchild) + 1;
return l > r ? l : r;
}
主函数实验类方法:
int main() {
tree T;
int n = 0;//叶子结点
int deep;//深度
BiTree PT = T.get_root();
cout << "先序遍历:";
T.PreOrderTraverse(PT); cout << endl;
cout << "中序遍历:";
T.InOrderTraverse(PT); cout << endl;
cout << "后序遍历:";
T.PostOrderTraverse(PT); cout << endl;
cout << "层序遍历:";
T.LevelOrderTraverse(PT); cout << endl;
cout << "叶子节点数:";
T.Count_TreeEnds(PT, n);
cout << n << endl;
BiTree exT;
exT = T.Exchange(PT);
cout << "交换后的先序遍历:";
T.PreOrderTraverse(exT); cout << endl;
cout << "该二叉树的深度:";
deep = T.Depth(exT); cout << deep << endl;
system("pause");
return 0;
}
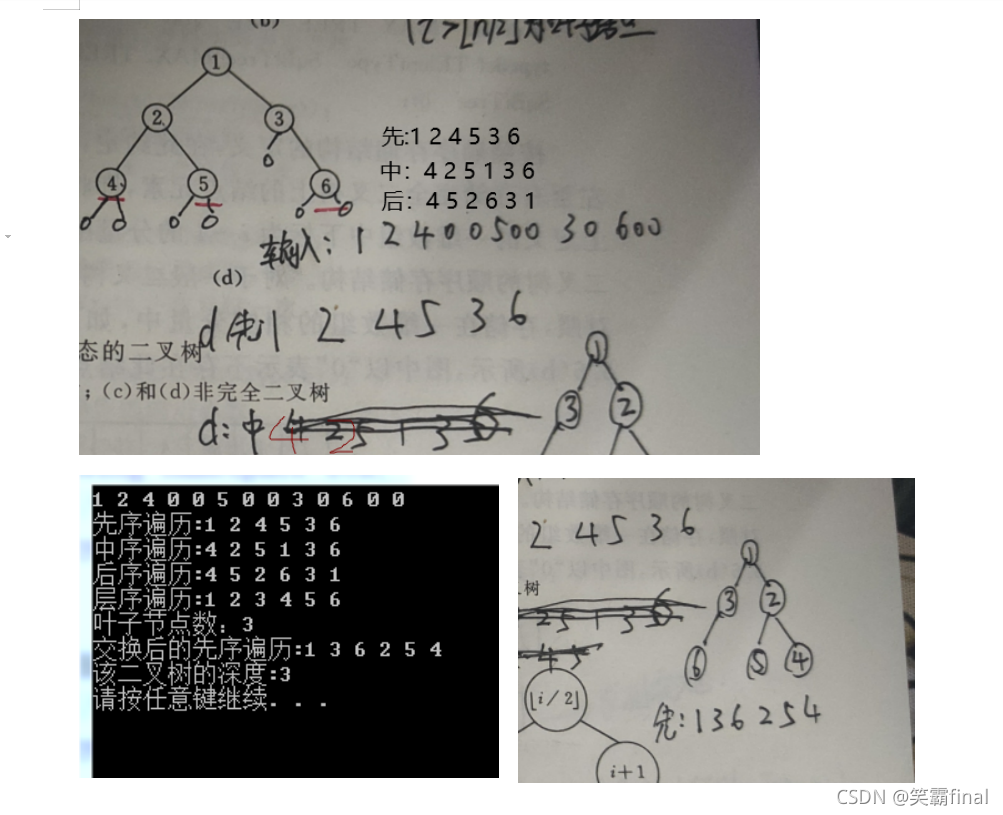
一些实验截图:

求求大家能
👍点赞👍 + 👀关注👀 + 🤏收藏🤏
