( 一 )有哪些数据类型

在前面的学习中我们已经了解了基本的内置类型,并知道了不同的内置类型的大小

char         //1byte

short        //2byte

int            //4byte

long         //4byte

long long //8byte

float         //4byte

double     //8byte 

这里有两点要注意的,就是int 和long类型的大小.C语言标准设定long类型的大小是大于等于int类型的大小的,并没有严格规定long类型的大小.而在16位机器上,int类型的大小是2个字节, ;在32位和64位的机器上,int类型的大小是4个字节.

1.类型的基本归类

①整型

char   --> signed char   unsigned  char

short  --> signed short   unsigned  short

int      -->  signed int       unsigned int

long   -->  signed long    unsigned  long

在整型中,数据又被分为有符号数和无符号数,有符号数可以加前缀signed来修饰,而无符号数可以加unsigned来修饰.不过,int,short,long这三个数据类型前面不加signed的时候默认是有符号数.char的情况比较特殊,他不加前缀修饰默认是什么类型是由编译器决定的,不过大多数的编译器是默认为有符号数.

关于有符号数和无符号数,这里还有一点很重要,在用printf打印时,打印无符号数是用%u作为占位符而不是%d,%d是打印有符号的十进制数.

 如上图,当用printf打印-10时,要用%u才能得出正确的结果.

②浮点数

float

double

 注意,浮点数跟整型不同,没有分为有符号数和无符号数,其实这是因为浮点数于整数在内存中的存储方式是不同的,这两种数据类型在内存中存储的差别我们会在后文详细讲解.

③构造类型

数组类型 --> int [10]

结构体  --> struct

枚举   --> enum

联合类型  --> union

 构造类型也被称为自定义类型,就是我们自己创造的类型.这里可能有一些读者会感到奇怪,难道数组也是一个类型吗?数组也是一个自定义类型吗?首先,我们来回答第一个问题,对于数组是不是一种类型,我们可以用sizeof来验证.

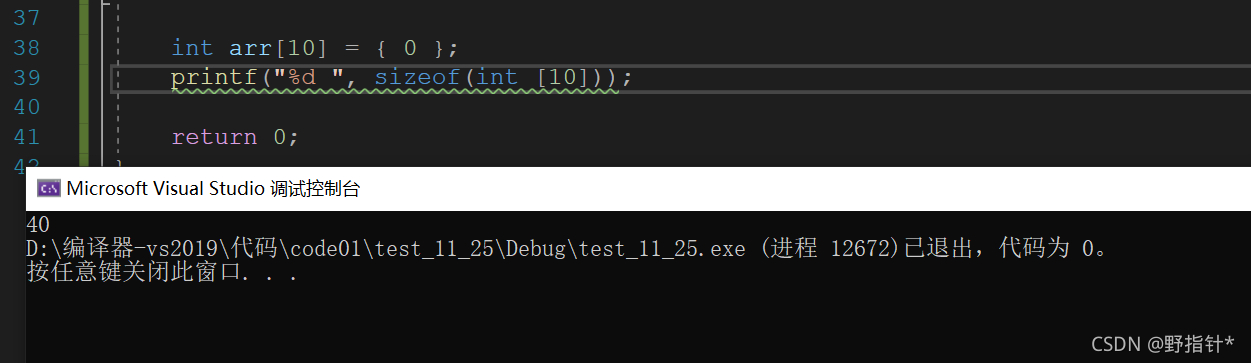
首先sizeof()括号内加上数据类型会计算出数据类型的大小,由上图我们不仅可以知道,数组也有类型,我们还知道,数组的类型是怎么表示的.

那么数组为什么是自定义类型呢?这个也很好理解,因为是由我们来决定数组中放多少个元素,是由我们来决定数组类型的大小的.其实数组和结构体很像,我们可以把结构体内的每个成员看成是类型不同的元素(也有可能相同),所以结构体和数组都是自定义类型.至于枚举类型和联合类型,我们后面会讲到,这两个其实和结构体很相似.

④指针类型

int *pi;

char *pc;

flaot *pf;

void *pv;

当然,我们这里只是列举了一部分的指针类型,还有其他的指针类型,比如二级指针,指向数组的指针,指向函数的指针等等,我们在这里不多赘述(后面会有更详细的讲解),在这里只要我们知道有这个类型就行.

⑤空类型

void 表示空类型

通常运用于函数的返回类型,函数的参数,指针类型

这里提一嘴void *类型,void * 类型是空类型的指针,对于这类指针,我们无法访问和对指针进行+-运算(因为我们不知道一次性对空类型的指针访问多大的空间,而且我们也不知道空类型的指针+-运算指针会往后走几个字节),NULL就是一个典型的空类型的指针,我们没办法对NULL指针进行解引用或者运算.

( 二 )整型在内存中的存储

1.原码,反码与补码

①原码,反码和补码之间的关系

无符号数:无原码反码和补码之说

有符号数正数:原码反码补码相同

有符号数负数:原码除了最高位(符号位)以外都按位取反,  反码 + 1得到补码

②原码,反码和补码的产生.整数类型被分为有符号数和无符号数,有符号数又被分为正数和负数,在计算机中有一个地方是专门执行运算的,在寄存器中,但是这块地方最开始只支持加法运算(例如:1 + 1),并不支持减法运算,科学家们为了节约成本(如果专门为减法设计电路的话,会导致成本上升),想出一个妙招,就是将减法运算变成加法运算(例如: 1 - 1 ---> 1 + (-1)),并规定有符号数的最高位为符号位,符号位为0表示正数,符号位为1表示负数,符号位参与运算.但是这样并没有解决问题:

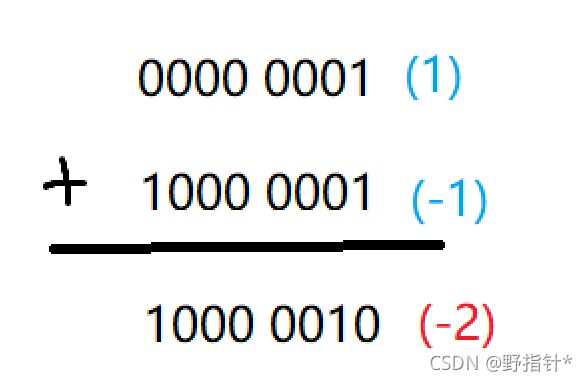
 1 + (-1)应该等于0,而不应该等于-2.于是科学家们发明了反码,就是让一个负数(为什么不是正数?因为在加法运算的时候,出现问题的是负数)除了最高位(符号位)以外的所有的位都按位取反.

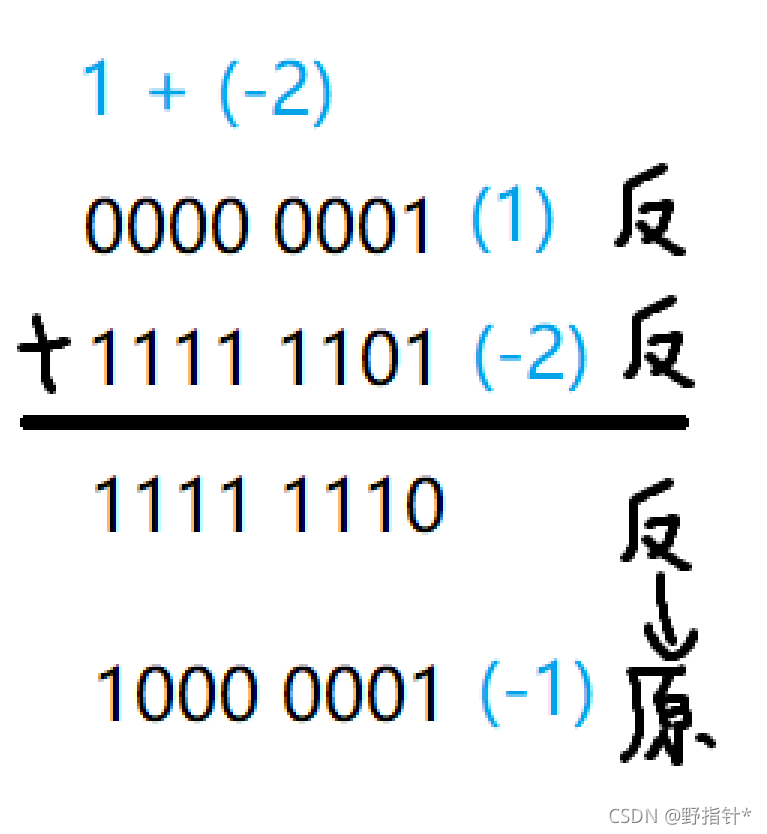
于是我们就大概地解决了减法变成加法这个问题,为什么说是大概呢?我们看一下下面的那个例子

 

1 + (-1)的结果是(-0),很明显,在我们正常的计算中,是不会出现-0这个结果的,-0也没有什么意义,科学家为了解决这个问题,又发明了补码.就是让反码 + 1.

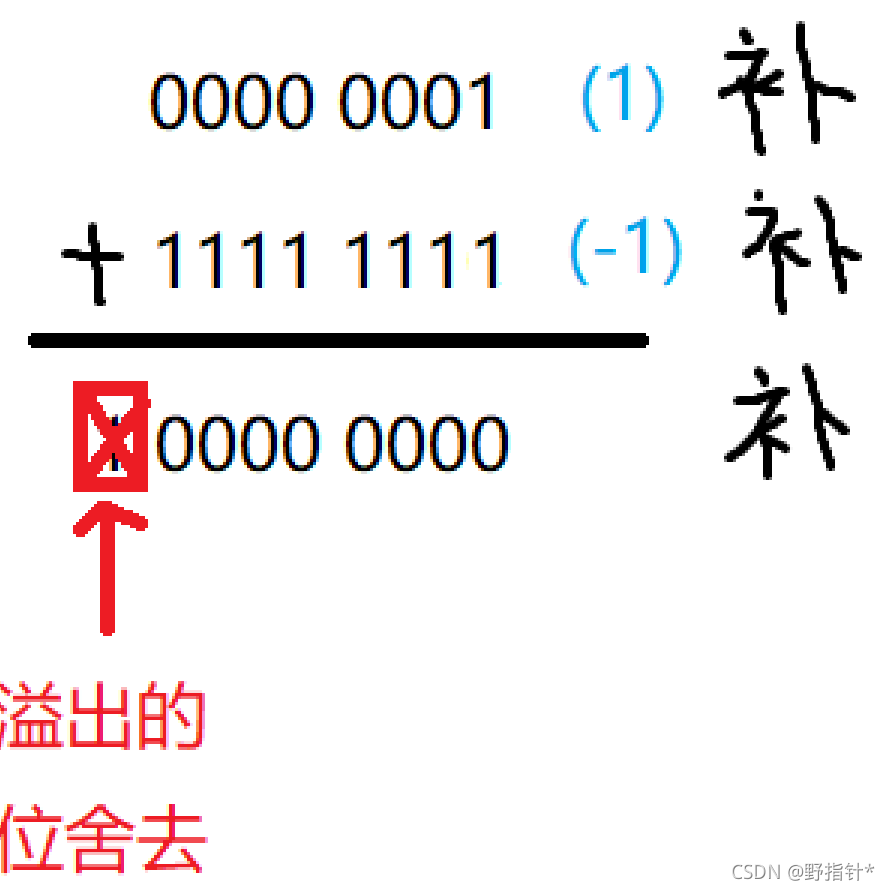
最后,这个问题被成功解决了,1 + (-1)最后的结果就是0, 由于0的最高位(符号位)是0,所以0是属于正数(尽管在数学中并非如此),0的原码,反码和补码都是他本身0.

到这里,可能有些读者会好奇,既然-0不存在了,那么1000 0000又变成了哪个数?

实际上,1000 0000变成了-128(补码),由于-128转换成原码是0,所以-128没有原码,只有补码.这样1000 0000(-0)变成了(-128),signed char可以存储的空间又大了一位,变成了[-128, 127],接下来,我们以char为例子,研究整型的数据存储范围.

2.整型的数据存储范围

整型被分为有符号数和无符号数,区别就是最高位到底是表示符号还是表示实实在在的值.

无符号char: 0000 0000 ~ 1111 1111(0 ~ 255),无符号char的数据存储类型比较简单明了

有符号char:(正数部分)0000 0000 ~ 0111 1111(0 ~ 127),(负数部分)1000 0000 ~ 1111 1111(-1 ~ -128)(这里要补充一点,有符号数在内存中都是以补码的形式存储的,以补码的形式进行运算的,以原码的方式进行输入输出).合起来就是(-128 ~ 127).

我们还留意到一点,当有符号char从0000 0000 变成 1111 1111的时候,其值是由0 变成 127 ,接着127变成-128,接着-128变成-1.我们对1111 1111再加上1,1111 1111就会变成0000 0000,也就是说,当我们不断地对有符号char +1,最终他会循环地从0变成127,127变成负数再变成0,我们可以用一张图来表示这样的关系.

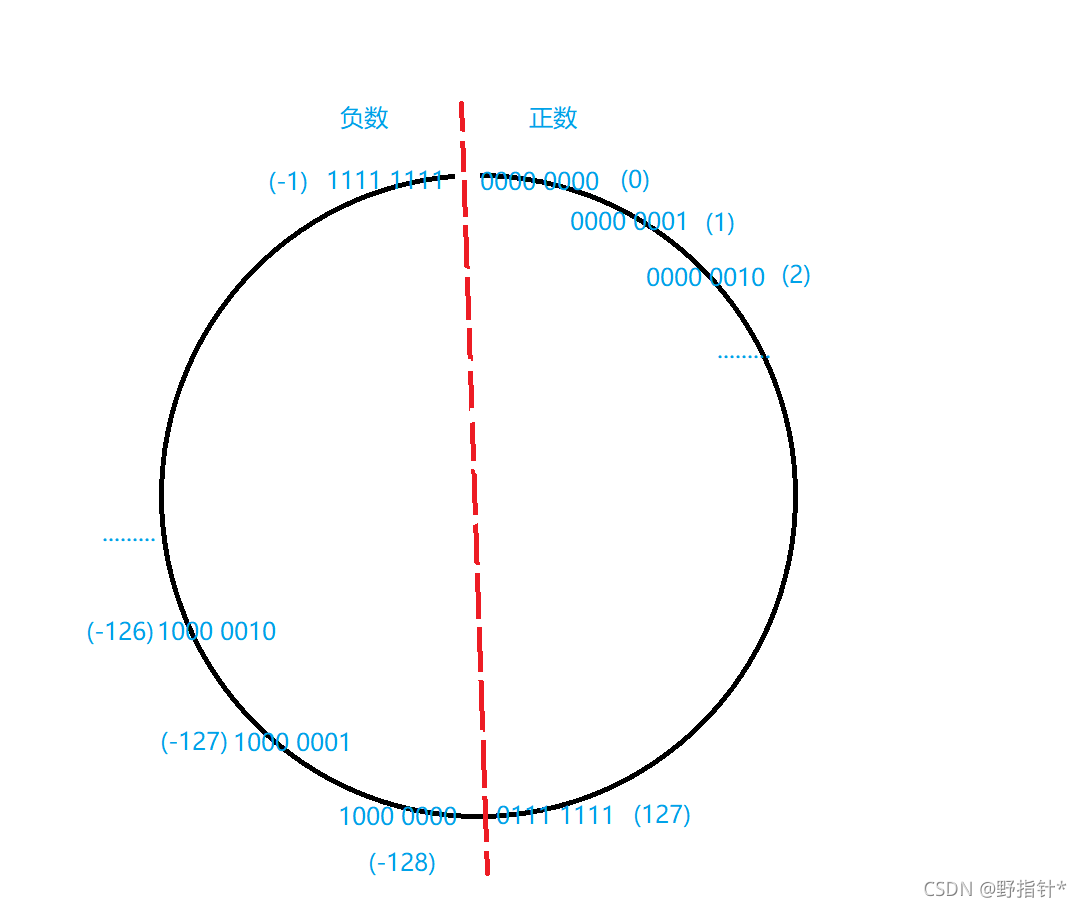
不仅是char类型,short, int ,long等等整形都是一样的,只不过他们表示的范围大了一些而已.

3.大小端存储模式介绍(大小大于1byte的整型)

我们知道,每个指针指向一个字节,我们可以通过指针来访问内存中存储的数据,那么我们对于大于1个字节的数据,我们该怎么通过指针访问呢?以int为例,

int a = 0x11223344

 计算机访问a的时候,到底是从11访问到44,还是44访问到11,还是用其他的顺序来访问呢?

首先,我们先排除第三种可能,因为如果不是按顺序来访问内存的话,那么计算机就需要记住访问内存的顺序,假如你是个设计计算机者,你会这么干吗?我想你不会自讨苦吃的,那么就剩下两种访问内存的可能性了,就是按从小到大的顺序来访问,或者按照从大到小的顺序来访问,指针访问的顺序又跟数据在内存中的存储的顺序有关,而这种顺序也被称为字节序.

根据字节序的不同,正数在内存中的存储被分为大端存储和小端存储.

大端存储的定义:低位的数据存储在高地址,高位的数据存储在低地址,这样的存储方式就叫做大端存储.

小端存储的定义:低位的数据存储在低地址,高位的数据存储在高地址,这样的存储方式就叫做小端存储.

我们这样说还是很抽象,我们举一个栗子.

 可以看到,0x11223344的低位44存储在低地址,而高位11存储在高地址.

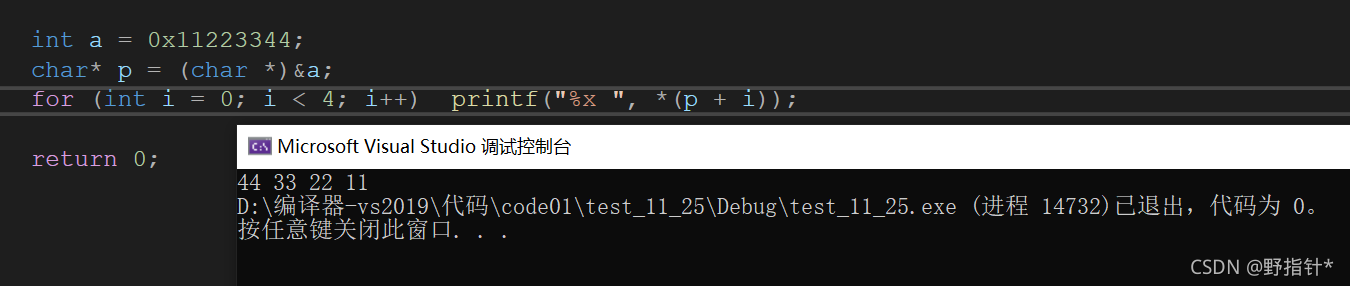
把他按字节从低地址到高地址一个个输出,果然,vs中数据是按照小端存储的方式来存储的(注意,一个编译器中数据只有一种存储的形式,不会一个地方小段存储一个地方大端存储的).

除了上面看起来有点复杂的输出数据的方法,我们有没有更简便的方法检测存储方式呢?

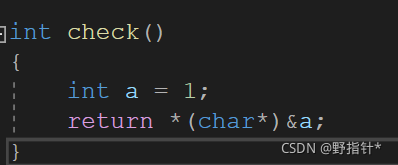
 当check()返回1的时候,是小端存储,否则是大端存储.

 注意:以上都是拿大于1个字节的整型来讨论大小端存储的,长度为1个字节或者小于1个字节的数据是没有大小端存储的这个说法的,因为指针访问这种类型的数据的时候没有顺序问题.

( 三 ) 浮点数在内存中的储存

在计算机中,没有小数这个说法,但是有浮点数这个说法.

我们看一看常见的浮点数

3.1415926

1E10

浮点数包括:float, double, long double类型

浮点数表示的范围:已经在float.h中定义

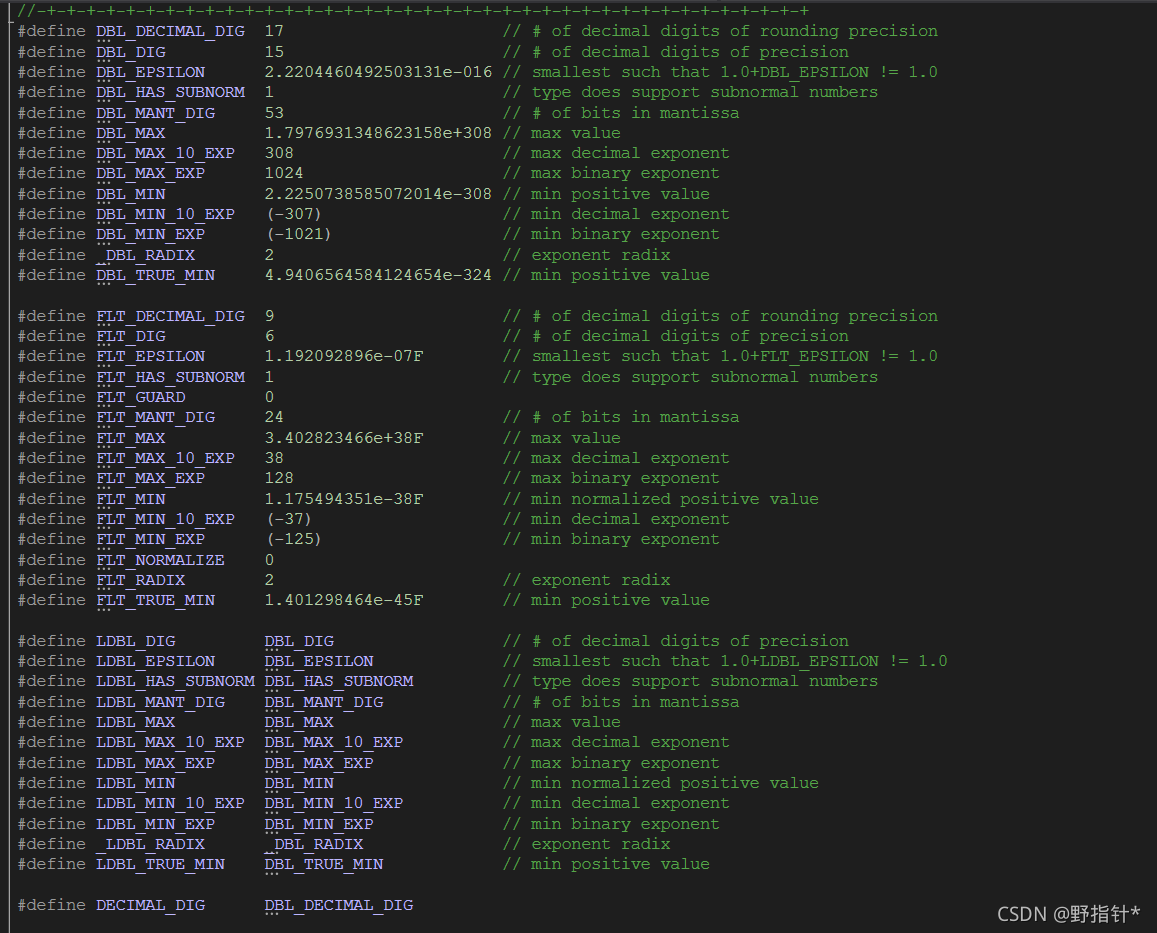
1.浮点数在内存中是如何存储的?

根据国际IEEE(电气和电子工程协会)754,任意一个二进制浮点数V可以表示为下面的形式:

①(-1)^S * M * 2^E

②(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。

③M表示有效数字，大于等于1，小于2。

④2^E表示指数位。

比如:在十进制中的5.0,把其变成二进制是101.0,也就是相当于(-1)^0 * 1.01 * 2^2

按照上面V的格式,S=0, M=1.01, E=2.

如果是-5.0,那么就是(-1)^1 * 1.01 * 2^2

S = 1,M = 1.01, E = 2;

(如果读者还是觉得这样很难理解,不妨可以类比一下十进制中的科学表示法)

①IEEE 754规定:

对于32位的浮点数,最高的1位是符号位,接着的8位是指数,剩下的23位是有效数字.

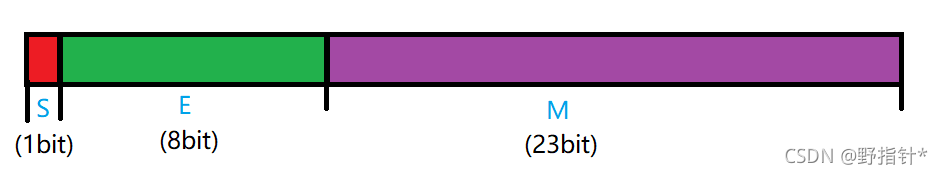
对于64位的浮点数,最高的1位是符号位,接着的11位是指数,剩下的52位是有效数字. 

②对于有效数字M和指数E,IEEE 754还有一些特别的规定:

在前面说过,1 <= M < 2,也就是说有效数字M一定是写成1.xxxxxx的形式.

IEEE 754规定,在计算机内部保存M时,默认最高数的第一位总是1,因此可以被舍去,就是把1.xxxxxx前面的1舍去,留下.xxxxxx,最后使用的时候再加上1(视情况)就可以了.

把第一位的1舍去之后,可以保留的有效数字就多了一位,变成了24位.

③对于指数E,情况就会比较复杂

首先,指数E是一个无符号整型(unsigned int)

但是,在科学计数法中会有指数为负数的情况,那么此时无符号整数就不能表示负数.

IEEE 754规定,32位浮点数在指数E存入内存时必须要加上一个值127,64位浮点数则要加上1023.

在把指数E从内存中取出来时又分为3种情况:

E不全都是0或者不全都是1:

此时,在取出E时会-127,得到最终结果

E全为0:

说明在将指数E存入内存之前的数非常小,时-127(或-1023),  2^(-127)(或2^(-1023))是一个极其趋近于0的数,那么此时,有效数字不再加上第一位的1,而是还原为0.xxxxxx的小数,这样做是为了表示+-0,以及非常接近于0的数.

E全为1:

此时如果有效数字M全为0(实际的有效数字是1),那么此时表示+-无穷大

2.有关于浮点数的一些补充

①浮点数的大小为4byte,8byte,那么会不会有像整型一样有类似的大小端问题呢?答案是肯定的,不过在这里就不是叫大小端存储了,在VS上,浮点数像是整数一样,浮点数的低位存储在低地址,高位存储在高地址.

②浮点数不能用关系操作符进行比较(大于,小于,等于),因为浮点数的存储必然有精度问题(32位浮点数只能存24位有效数字,64位浮点数只能存53位有效数字),我们无法得知(以我们当前学的知识)在这个精度以外的数字是什么,所以我们无法通过关系操作符得出两个浮点数谁大谁小.

那么,有什么办法可以解决这个问题吗?有!就是相减,让两个浮点数相减,当得到的值小于某个我们人为规定的值时,那么我们就认为这两个浮点数是相等的,我们也可以通过比较两数相减的值的正负来判断这两个数谁大谁小.

以上是有关于数据在内存中存储的介绍,如果有不妥之处欢迎在评论区中指出~~~