物理层

2.1 物理层的基本概念

物理层考虑的是怎样才能在连接各种计算机的传输媒体上传输数据比特流。

物理层为数据链路层屏蔽了各种传输媒体的差异，使数据链路层只需要考虑如何完成本层的协议和服务,而不必考虑网络具体的传输媒体是什么。

物理层协议的主要任务：

• 机械特性：指明接口所用接线器的形状和尺寸、引脚数目和排列、固定和锁定装置。

• 电气特性：指明在接口电缆的各条线上出现的电压的范围。

• 功能特性：指明某条线上出现的某一电平的电压表示何种意义。

• 过程特性：指明对于不同功能的各种可能事件的出现顺序。

2.2 数据通信的基础知识

传输方式

串行传输 和 并行传输：

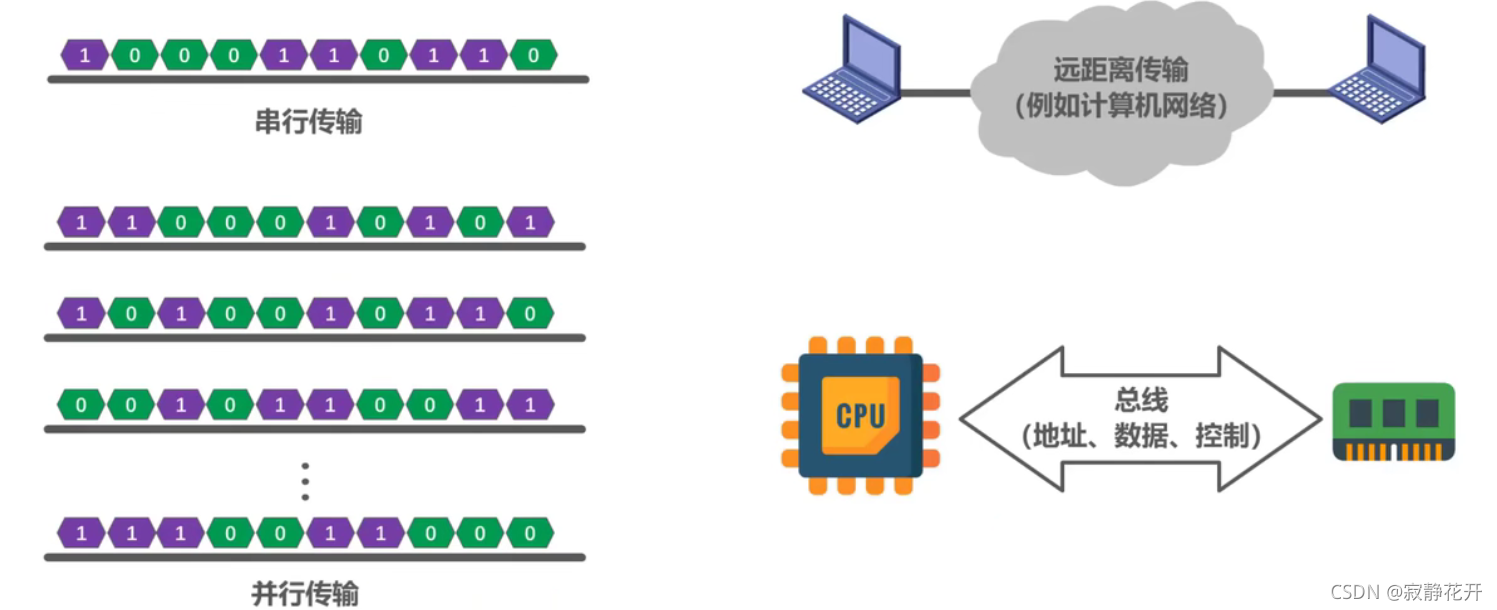
同步传输 和 异步传输：

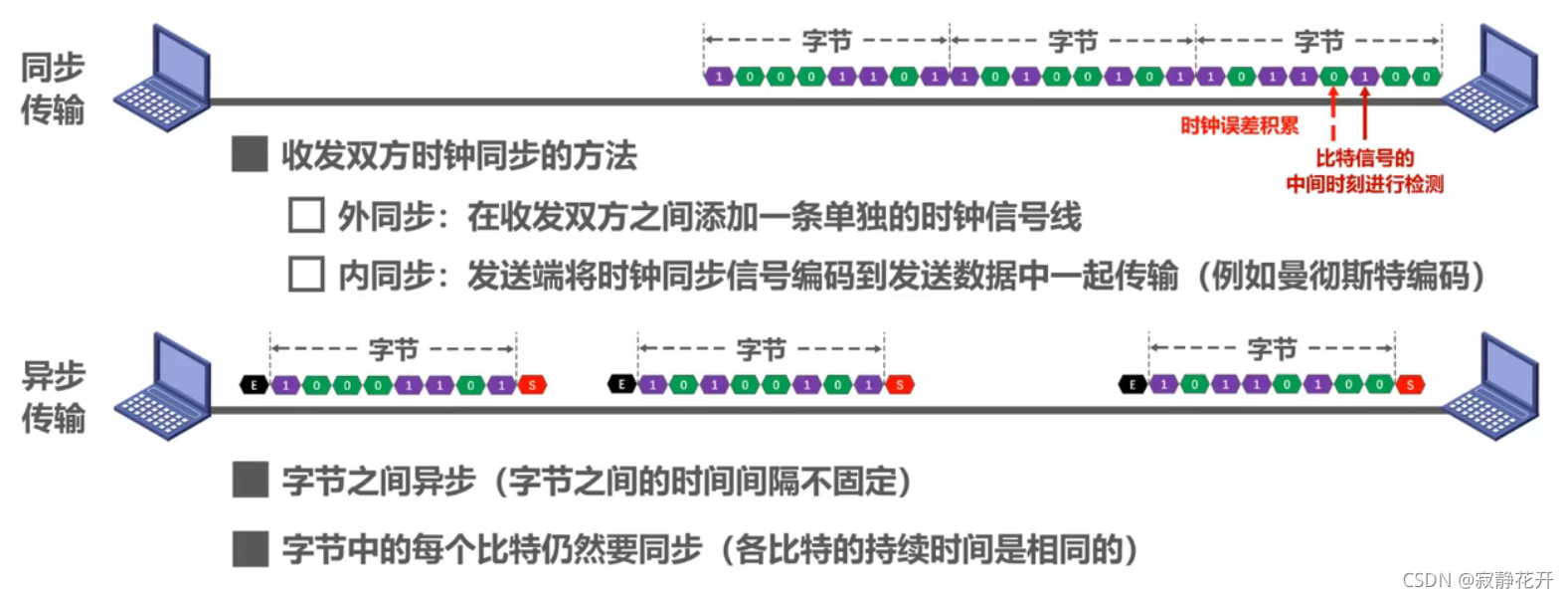
单向通信（单工）：只能有一个方向的通信而没有反方向的交互。
例：无线电广播、有线电广播、电视广播

双向交替通信（半双工）： 通信的双方都可以发送信息，但不能双方同时发送(当然也就不能同时接收)。
例：对讲机

双向同时通信（全双工）：通信的双方可以同时发送和接收信息。
例：电话

常用术语

数据：运送消息的实体。
信号：数据的电气的或电磁的表现。
模拟信号： 代表消息的参数的取值是连续的。
数字信号：代表消息的参数的取值是离散的。
码元： 在使用时间域(或简称为时域)的波形表示数字信号时，代表不同离散数值的基本波形。
信道： 一般用来表示向某一个方向传送信息的媒体。

编码与调制

基本编码

不归零制：正电平代表1，负电平代表0。
归零制：正脉冲代表1，负脉冲代表0。
曼彻斯特编码：位周期中心的向，上跳变代表0，位周期中心的向下跳变代表1。但也可反过来 定义。
差分曼彻斯特编码：在每一位的中心处始终都有跳变。位开始边界有跳变代表0，而位开始边界没有跳变代表1。

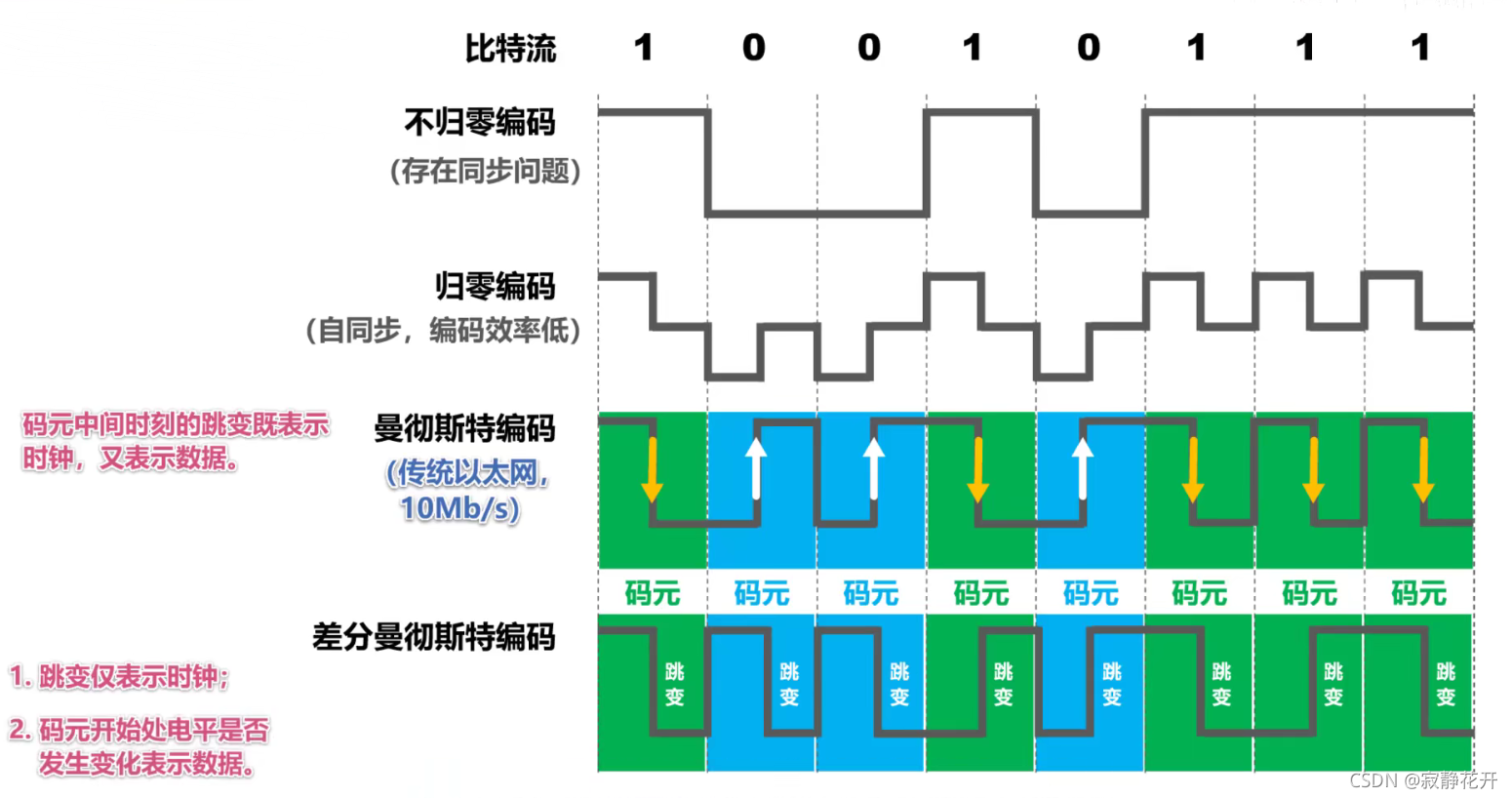
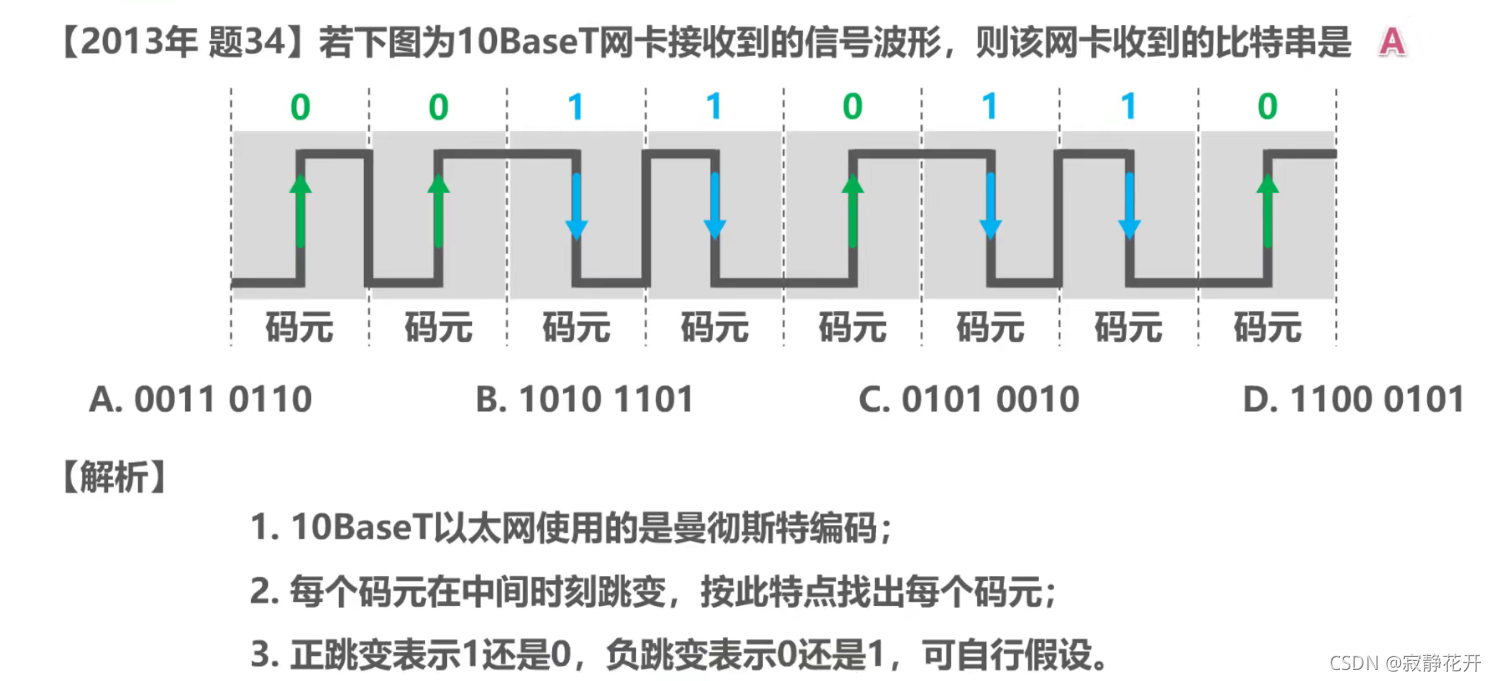
基本调制

基带信号往往包含有较多的低频成分，甚至有直流成分，而许多信道并不能传输这种低频分量或直流分量。为了解决这一问题，就必须对基带信号进行调制(modulation)。
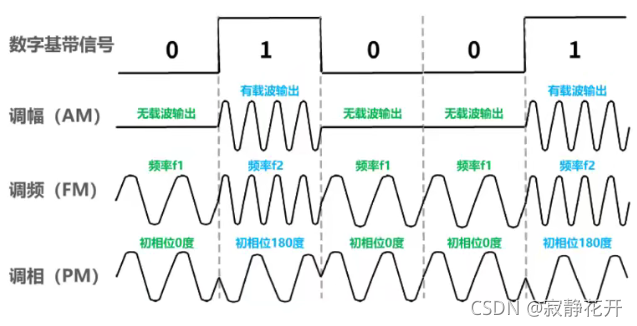
最基本的二元制调制方法有以下几种:
调幅(AM)：载波的振幅随基带数字信号而变化。
调频(FM)：载波的频率随基带数字信号而变化。
调相(PM) ：载波的初始相位随基带数字信号而变化。

2.3 物理层下面的传输媒体

导引型传输媒体：同轴电缆、双绞线、光纤、电力线

同轴电缆价格较贵且布线不够灵活和方便，随着集线器的出现，在局域网领域，基本上都是采用双绞线作为传输媒体。

双绞线 绞合的作用：

1. 抵御部分来自外界的电磁波干扰
2. 减少相邻导线的电磁干扰

光纤的优点：

• 通信容量大 (25000~ 30000GHz的带宽)
• 传输损耗小，远距离传输时更加经济。
• 抗雷电和电磁3 F扰性能好。这在大电流脉冲干扰的环境下尤为重要。
• 无串音干扰， 保密性好，不易被窃听。
• 体积小，重量轻。

光纤的缺点：
割接需要专用设备
光电接口接口较贵

非导引型传输媒体：无线电波、微波、红外线、可见光

2.4 信道复用技术

任何实际的信道都不是理想的，在传输信号时会产生各种失真以及带来多种干扰。

失真的原因：

• 码元传输的速率越高
• 信号传输的距离越远
• 传输媒体质量越差
• 噪声干扰

限制码元在信道上的传输速率的因素:

• 信道能够通过的频率范围
• 信噪比

信道分类

1.广播信道
一对多通信，一个节点发送的数据能够被广播信道上所有的节点接收到。

所有的节点都在同一个广播信道上发送数据，因此需要有专门的控制方法进行协调，避免发生冲突（冲突也叫碰撞）。

主要有两种控制方法进行协调，一个是使用信道复用技术，一是使用 CSMA/CD 协议。

2.点对点信道
一对一通信。

因为不会发生碰撞，因此也比较简单，使用 PPP 协议进行控制。

信道复用

1.频分复用

频分复用的所有主机在相同的时间占用不同的频率带宽资源。

2. 时分复用

时分复用的所有主机在不同的时间占用相同的频率带宽资源。

使用频分复用和时分复用进行通信，在通信的过程中主机会一直占用一部分信道资源。但是由于计算机数据的突发性质，通信过程没必要一直占用信道资源而不让出给其它用户使用，因此这两种方式对信道的利用率都不高。

3. 统计时分复用

是对时分复用的一种改进，不固定每个用户在时分复用帧中的位置，只要有数据就集中起来组成统计时分复用帧然后发送。

4. 波分复用

光的频分复用。由于光的频率很高，因此习惯上用波长而不是频率来表示所使用的光载波。

5. 码分复用

为每个用户分配 m bit 的码片，并且所有的码片正交，对于任意两个码片 S和 T有

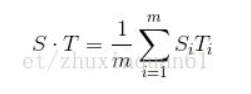
和向量一样规格化内积。
（会考计算：点击连接 计算题）

2.5 & 2.6 就考试来说不重要