蓝桥杯 ALGO-1005 数字游戏 python
试题 算法训练 数字游戏
资源限制
时间限制:1.0s 内存限制:256.0MB
问题描述
给定一个1~N的排列a[i],每次将相邻两个数相加,得到新序列,再对新序列重复这样的操作,显然每次得到的序列都比上一次的序列长度少1,最终只剩一个数字。
例如:
3 1 2 4
4 3 6
7 9
16
现在如果知道N和最后得到的数字sum,请求出最初序列a[i],为1~N的一个排列。若有多种答案,则输出字典序最小的那一个。数据保证有解。
输入格式
第1行为两个正整数n,sum
输出格式
一个1~N的一个排列
样例输入
4 16
样例输出
3 1 2 4
数据规模和约定
0<n<=10
解题思路
其实这道题,我真的是跌宕起伏,如果是C++我可能早就写出来了吧,但是由于是python,很多解就不能暴力搜索了,要不然1-10的暴力搜索也不是不可以,孩子快哭了,不过无所谓,就当锻炼算法吧
首先给出两个70分的代码,在这两个code之中,都有一些比较好的思想,第一个就是可以直接利用我们内置库函数,对我们给出的数组进行一个全排列,然后我们直接累加迭代发现sum一样不就可以了么,这多么简单啊,还要搞什么呀哈哈哈,结果70分,有些案例就是过不了,时间直接TLE,让人绝望啊,先给出代码,代码思想很简单,就是得到全排列然后累加求和
内置库运用70分
import itertools
a = list(range(1,n+1))
n,sum = map(int,input().split())
for l in itertools.permutations(a,n):
l = list(l)
# print(l)
l2 = l[:]
for i in range(n-1):
for j in range(n-1-i):
l[j] += l[j+1]
if l[0] == sum:
for i in l2:
print(i,end=' ')
break
结果只有70分
然后行吧,用点算法吧,用搜索咯,那肯定是比较常见又简单的DFS咯,很简单的想法,我们可以在本身的数组上进行一个累加,这样最后得到的结果元素1也就是我们的s[0] 如果是sum的时候,我们就可以直接打印出结果了。
然后后面一段就是用dfs思想了,如果visit过了就换一个的,不断的迭代,直到有n个数据,我们才进行判断
DFS 70分
s = [0]*n
d = [0]*n
vis = [0]*n
n,sum = map(int,input().split())
def dfs(step):
if step == n:
s = d[:]
for i in range(n-1):
for j in range(n-1-i):
s[j] += s[j+1]
if s[0] == sum:
print(' '.join(str(i) for i in d))
return True
else:
return False
for i in range(0,n):
if vis[i] == 1:
continue
vis[i] = 1
d[step] = i + 1
if dfs(step+1):
return True
vis[i] = 0
return False
dfs(0)
但是结果还是差强人意,虽然会比上面的时间复杂度低一点,但是还是70分啊,还有样例还是过不了,我差点绝望了,我就看啊看,到底有什么算法可以解决。其实对于我们的程序来说,最耗时间的一部分第一个是我们的赋值,我们的d赋值可以利用append,pop这些时间比较少的,其次就是我们求和那一部分是一个二重循环,时间复杂度比较高。
然后我就思前想去,突然,我在想,每一行中的数据求和与我们最后得到的和有什么关系么,后面,我终于悟到了,杨辉三角!!!
这不就是一个典型的杨辉三角么,按样例来看,杨辉三角的底层是1 3 3 1,求和就是3x1 + 1x3+ 2x3 + 4x1 = 16,哇,这么说的话,其实我并不用算太多,我可以直接进行一个计算杨辉三角的底层,只有一个循环,这就简单了
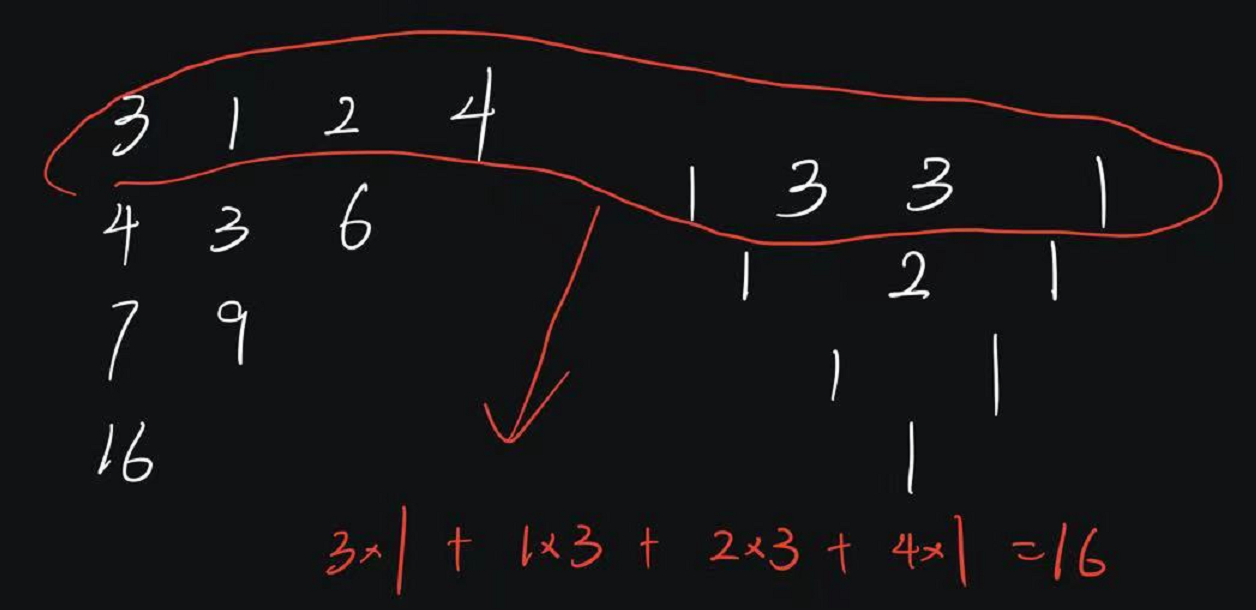
所以首先小小改进了一下
改进的90分代码
# return 杨辉三角的最后一行
def yh(num):
if num == 1:
res = [1]
else:
res = [[0]*num for i in range(num)]
for i in range(num):
for j in range(num):
res[i][0] = 1
if i == j:
res[i][j] = 1
for i in range(2,num):
for j in range(1,i):
res[i][j] = res[i-1][j-1] + res[i-1][j]
return res[num-1]
n,sum = map(int,input().split())
yh = yh(n)
d = [0]*n
vis = [0]*n
def dfs(step):
if step == n:
s = 0
for i in range(n):
s += d[i]*yh[i]
if s == sum:
print(' '.join(str(i) for i in d))
return True
else:
return False
for i in range(0,n):
if vis[i] == 1:
continue
vis[i] = 1
d[step] = i + 1
if dfs(step+1):
return True
vis[i] = 0
return False
if n == 1:
print(sum)
else:
dfs(0)
结果还是大意了,只有80,所以其实在我们的DFS中,我们还需要一些剪枝之类的操作才可以得到比较好的结果,所以用同样的想法进行一个改进,最后终于圆满了,我们可以在本身要计算的时候,传入的就是求和的结果,如果大于我们需要的sum就直接break,也就是剪枝了,这样可能就比较好,减少了循环的计算。
完美的100分代码
# return 杨辉三角的最后一行
def yh(num):
if num == 1:
res = [1]
else:
res = [[0]*num for i in range(num)]
for i in range(num):
for j in range(num):
res[i][0] = 1
if i == j:
res[i][j] = 1
for i in range(2,num):
for j in range(1,i):
res[i][j] = res[i-1][j-1] + res[i-1][j]
return res[num-1]
n,sum = map(int,input().split())
yh = yh(n)
d = []
vis = [0]*(n+1)
def dfs(step,s):
if s > sum:
return False
if step == n:
if s == sum:
print(' '.join(str(i) for i in d))
return True
else:
return False
for i in range(1,n + 1 ):
if vis[i] == 0:
vis[i] = 1
d.append(i)
if dfs(step+1,s+yh[step]*i):
return True
vis[i] = 0
d.pop()
return False
if n == 1:
print(sum)
else:
dfs(0,0)
所以最后终于AC了,结束了,good,还好成功了,没有放弃
每日一句
What doesn’t kill you makes you stronger.
没能摧毁你的,必使你强大。