排序

常见的排序算法

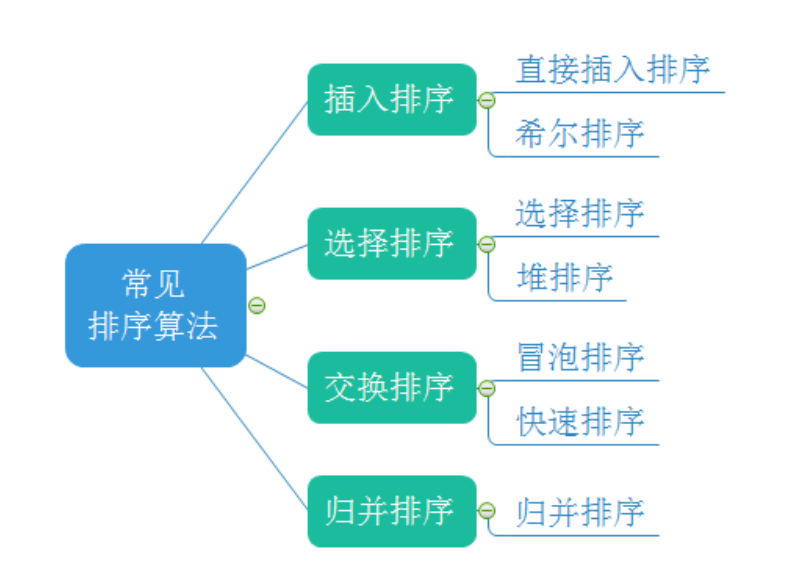
常见排序算法的实现

冒泡排序 也是我们本身接触最早的排序 很简单的一个排序

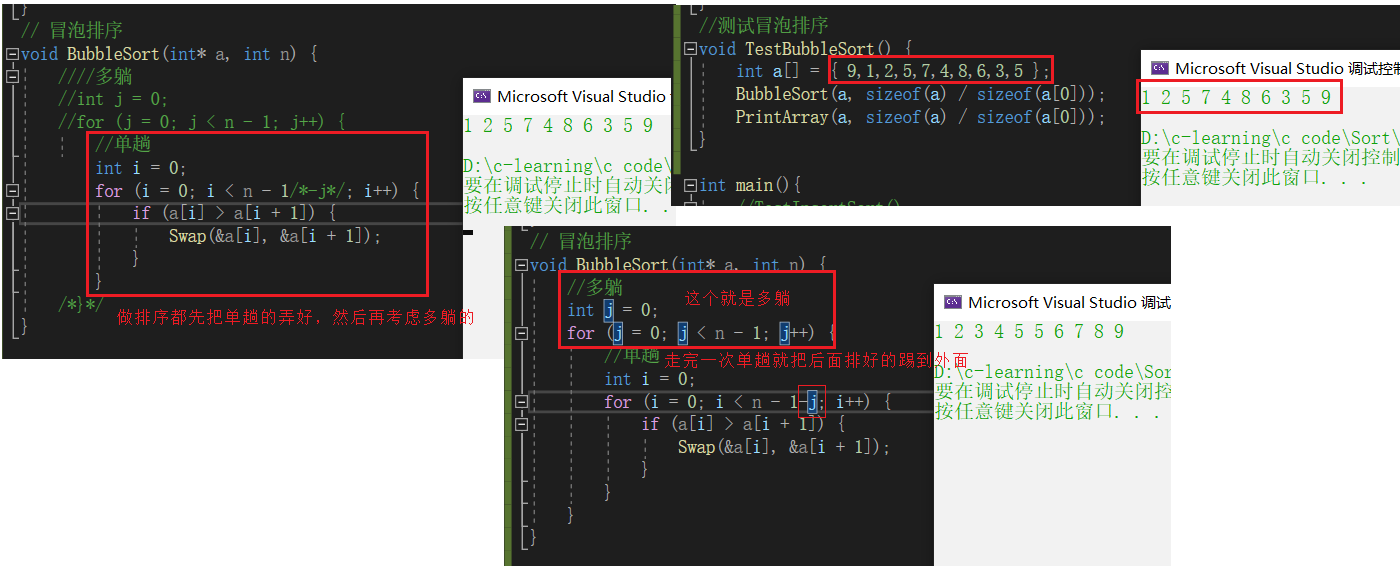
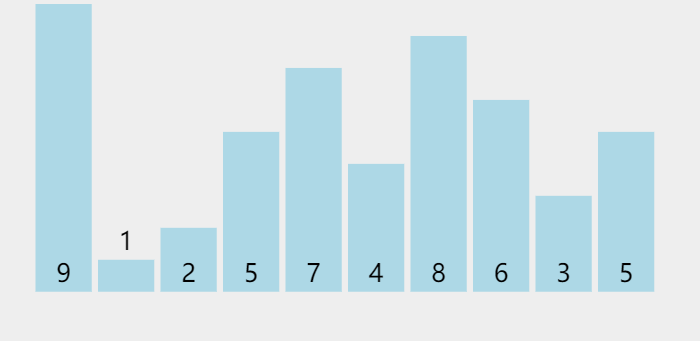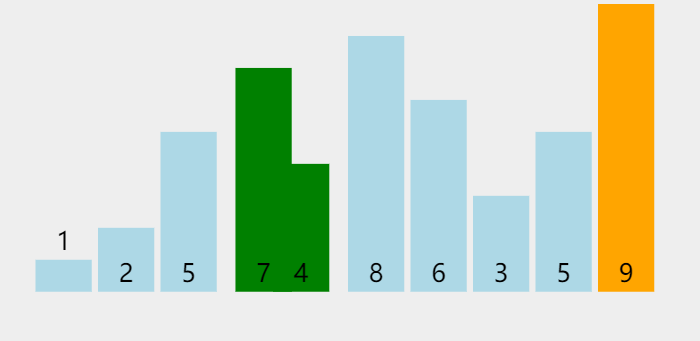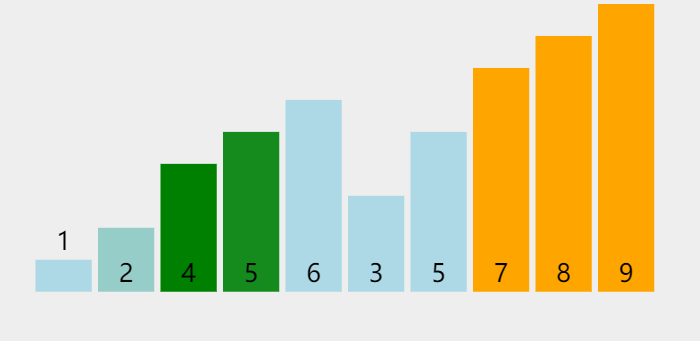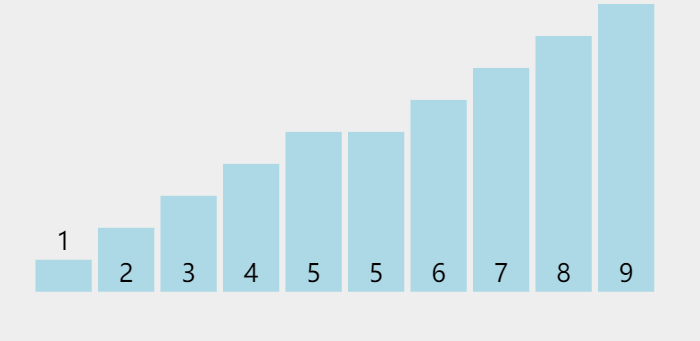
// 冒泡排序
void BubbleSort(int* a, int n) {
	//多躺
	int j = 0;
	for (j = 0; j < n - 1; j++) {	
		//单趟
		int i = 0;
		for (i = 0; i < n - 1-j; i++) {
			if (a[i] > a[i + 1]) {
				Swap(&a[i], &a[i + 1]);
			}
		}
	}
}

但是我们可以优化一下吗，就是原本就是有序的情况下，我们还要走多趟吗 ？反正上面的代码是必走的

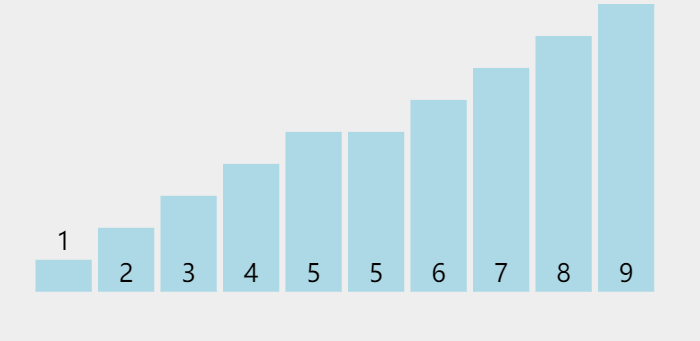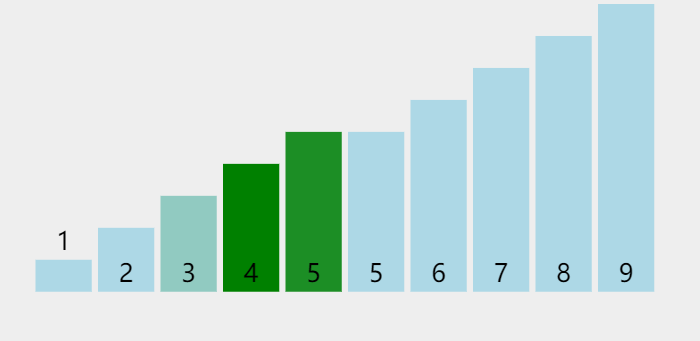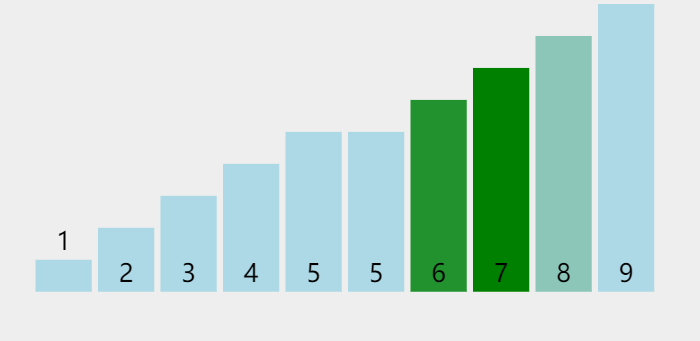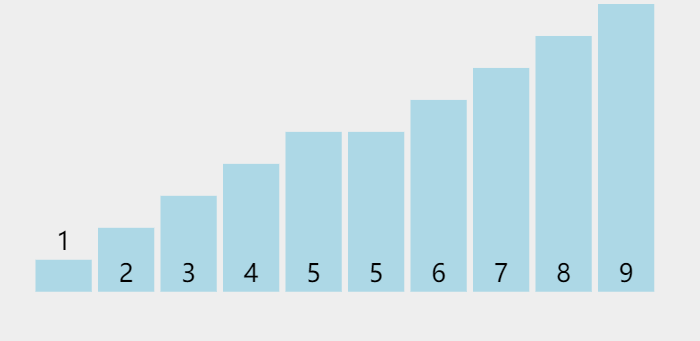
我们可以发现正常的是只要遍历一次发现有序了就不会再来第二遍，所以我们要优化一下代码

加了标记后，就可以达到上面那个动图遍历一遍没有变化就直接出来的效果

完整冒泡排序代码

// 冒泡排序
void BubbleSort(int* a, int n) {
	//多躺
	int j = 0;	
	for (j = 0; j < n - 1; j++) {	
		//交换标记变量
		int flag = 0;
		//单趟
		int i = 0;
		for (i = 0; i < n - 1-j; i++) {
			//交换标记改变
			flag = 1;
			if (a[i] > a[i + 1]) {
				Swap(&a[i], &a[i + 1]);
			}
		}
		//标记还是0就跳出
		if (!flag)
			break;
	}
}

冒泡排序时间复杂度O(N²)

最好：O(N)

最坏：O(N²)

到再来我们可以把同级别的插入排序，选择排序，冒泡排序拉出来对比一下

横向对比

选择最差，因为无论最好还是最坏都是O(N²)

直接插入和冒泡最好情况下是O(N)，最坏是O(N²)

但是肯定有人也想比较一下直接插入和冒泡

**在已经有序的情况下：**两个是一样好的

**在接近有序的情况下：**直接插入比冒泡要好，因为单一个找到需要插（交换）的，直接插入就直接插入，然后就不需要再跑了；然而冒泡还要排序到尾部，这就是比直接插入比有点小小的不如的地方

快速排序（无敌的排序）

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

将区间按照基准值划分为左右两半部分的常见方式有：

1. hoare版本
2. 挖坑法
3. 前后指针版本

1.hoare版本（发明快排的人用的方法）

一般选最左边/最右边做key。

任何排序都要先考虑第一趟，只有跑了第一趟才会有后面的趟数。==单趟排序的目标是：==key左边的值要比key小，key右边的值要比key要大。

最左边做key

最右边做key

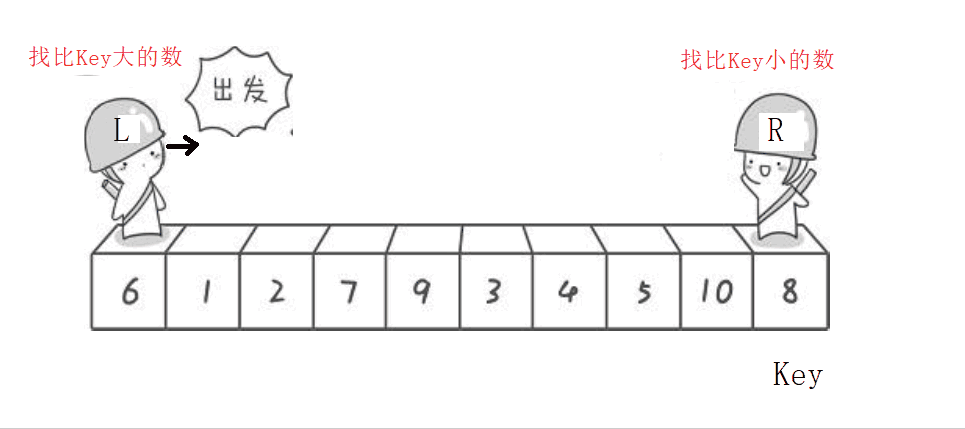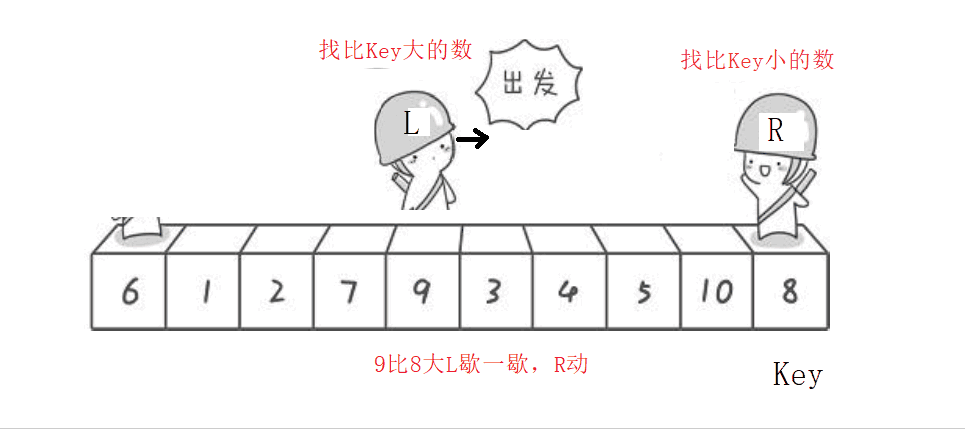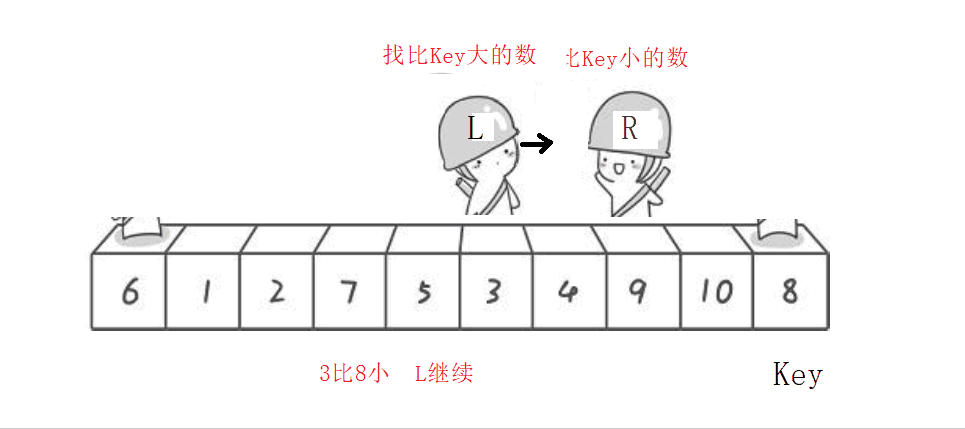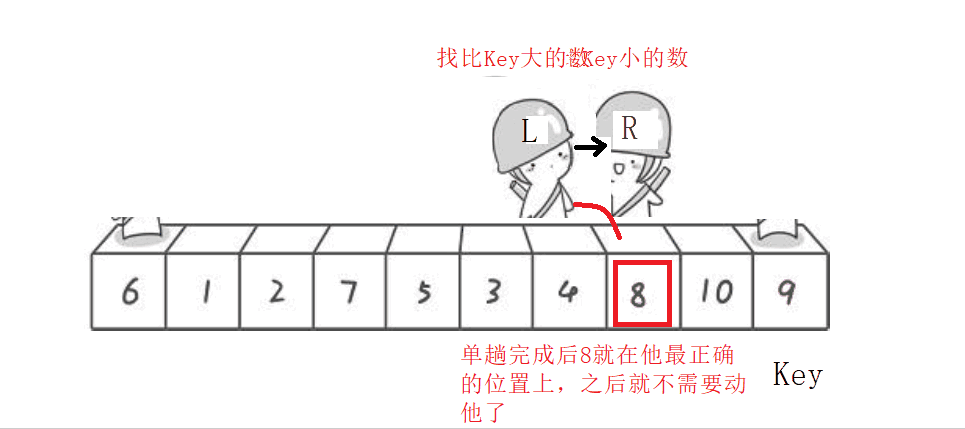
实际上上面那个动图我是知道先动哪个再动哪个，不想再画第二遍的哈哈

选左边的值做key，右边先走—>左右相遇时的值要比key小

选右边的值做key，左边先走—>左右相遇时的值要比key大

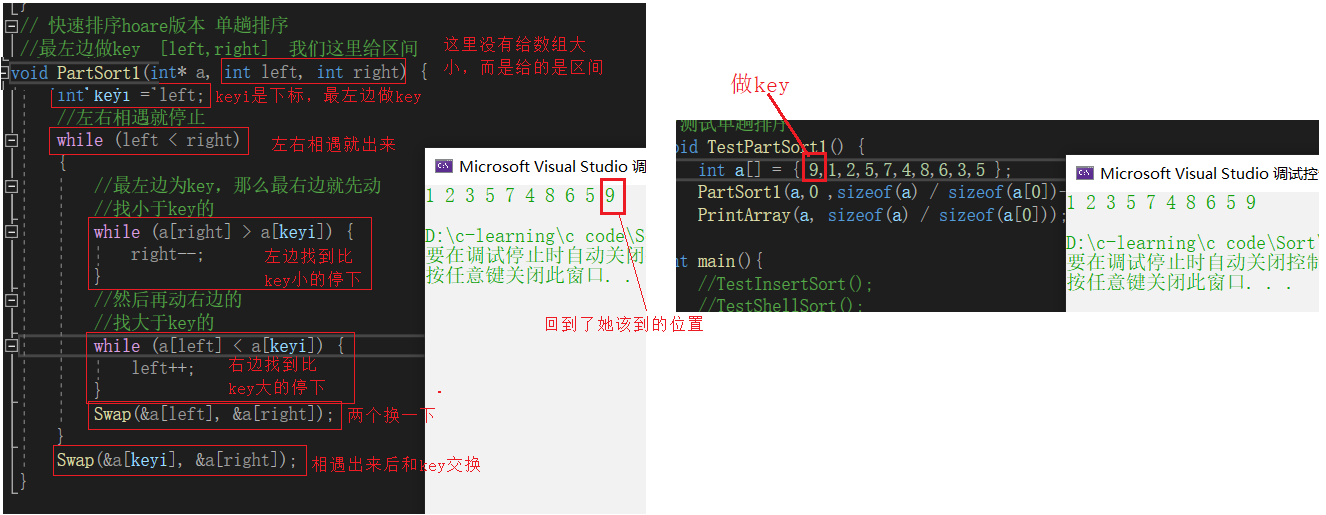
但是上面是有点瑕疵的大方向没有错，但是细节还是没有处理好，我们称之为极端情况

1.一模一样元素的数组

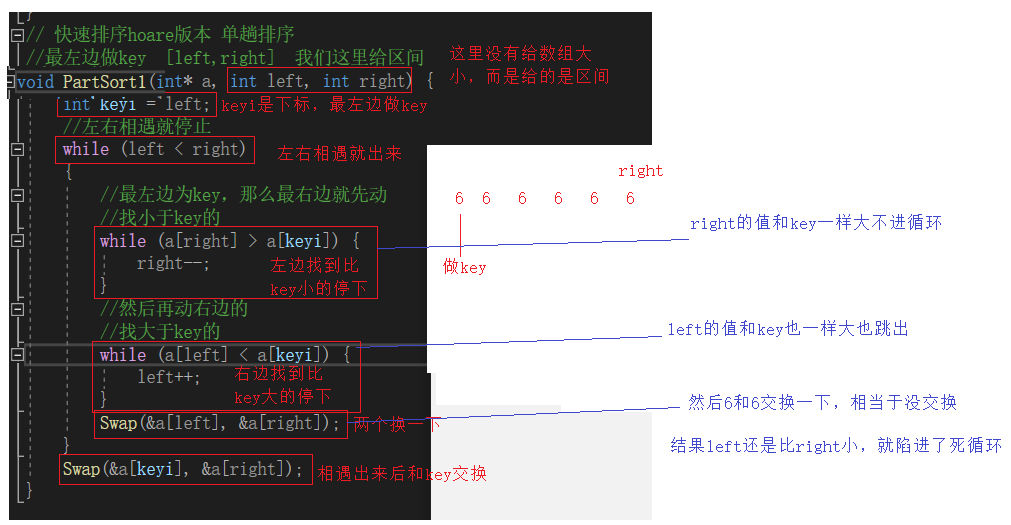
既然相等就跳出了，不是我们要的小的才能跳出，那么我们就把相等也放进循环里面，因为只有在循环里面right才会–，left才会++

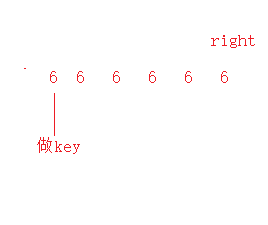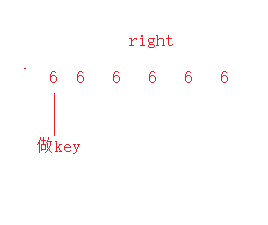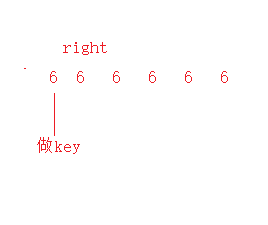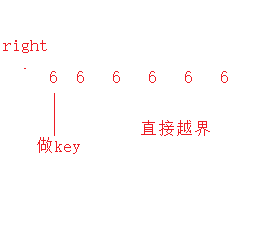
所以为了不让程序出界 循环中并上left<right

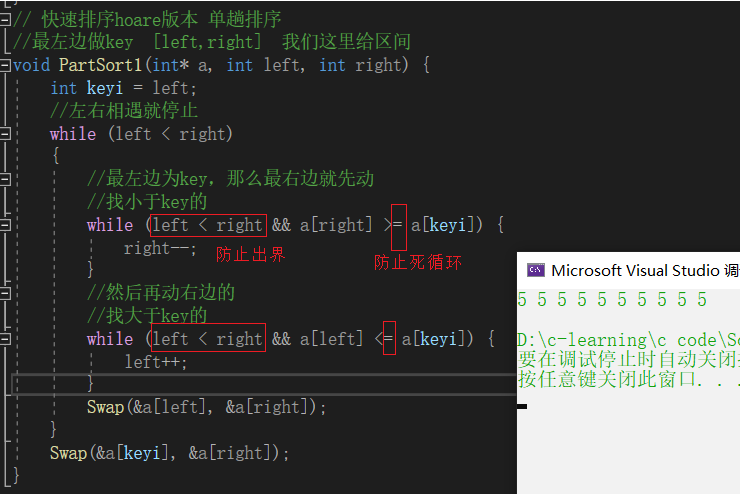
单趟时间复杂度是：O(N)

上面的单趟排序已经排完，比key小的都放到了左边，比key大的都放到了右边

我们的目的是让左子空间和右子空间都有序，这样整体就有序了

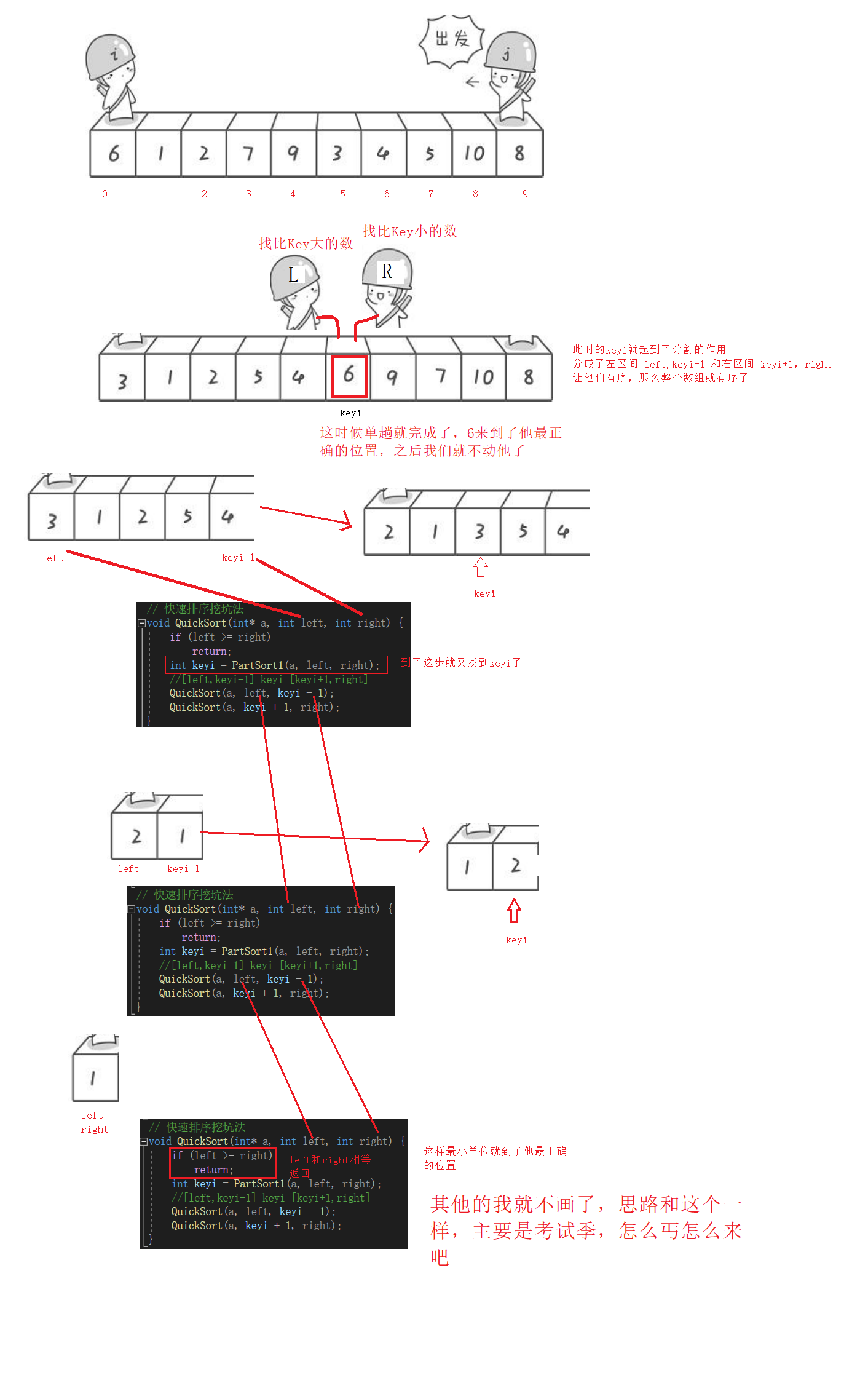
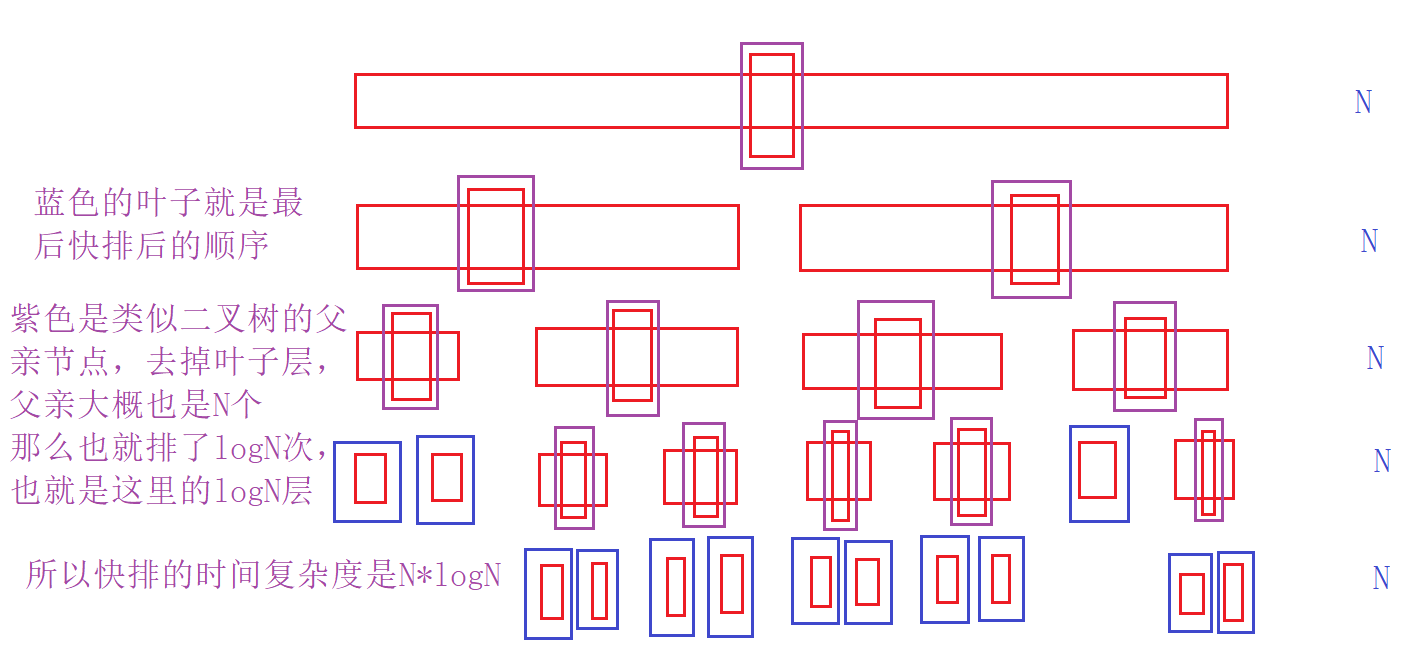
快排时间复杂度：O(N*logN)

测性能

到了我最喜欢的测性能的时候了看看到现在的所有排序的性能 当然都是在release里面测的

选1000 一千

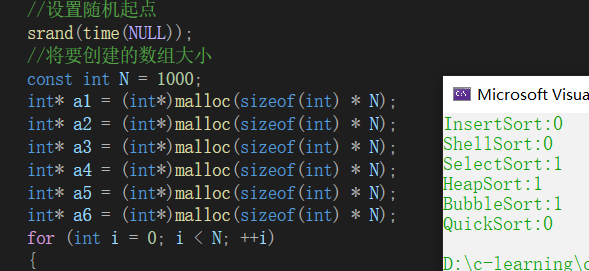
选10000 一万

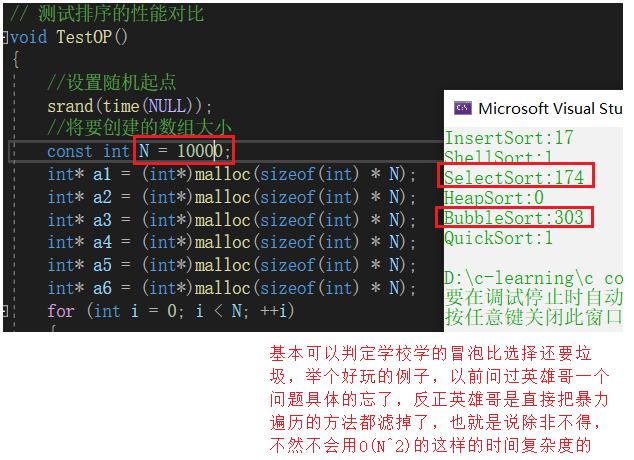
选100000 十万

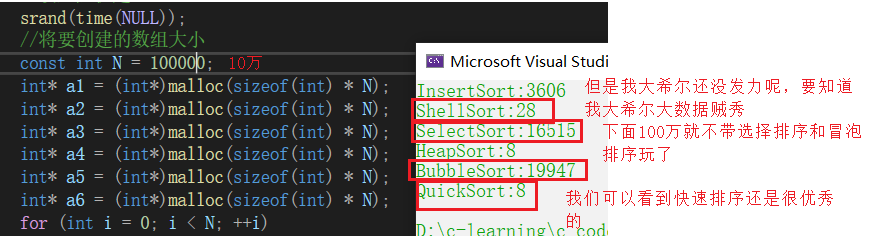
选1000000 一百万

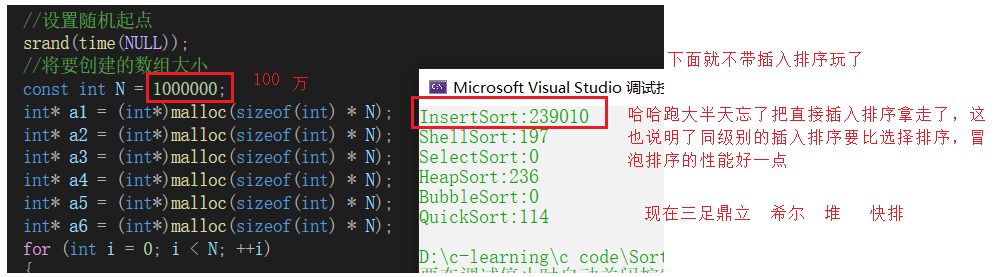
选10000000 一千万

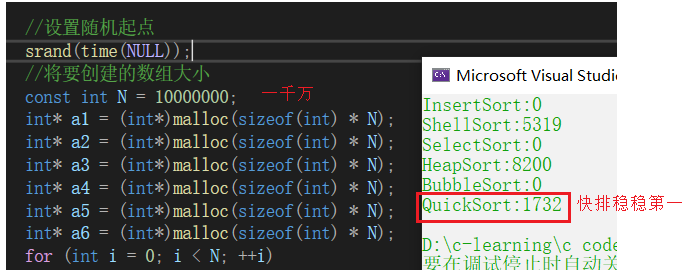
但是想想上面快排有没有什么缺陷 明明是秒男还想在特殊情况下当持久男 哈哈

既然是交换排序，那么就会出现和冒泡排序一样的问题，开始就是有序的问题

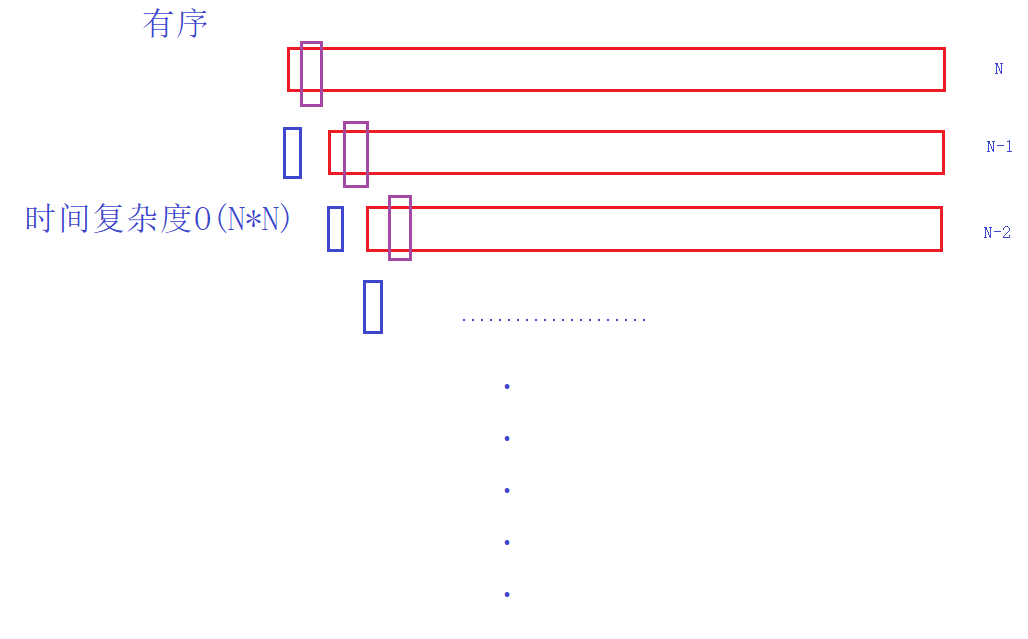
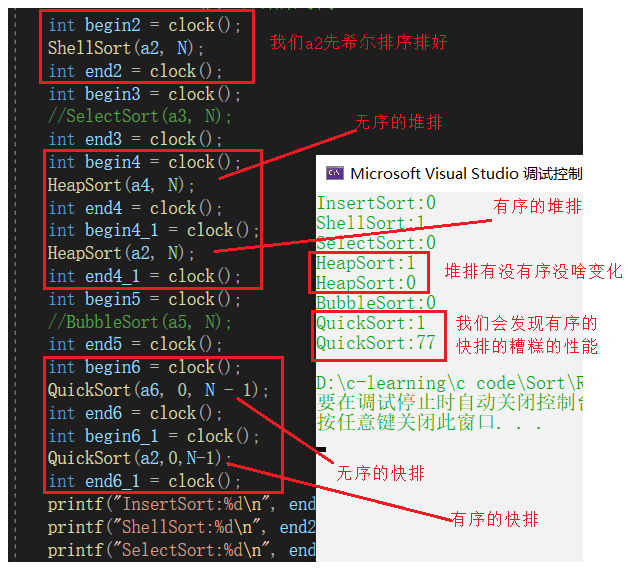
如何解决快排面对有序的选Key问题

1.随机选Key 把命运交给随机，我和你说我直接不考虑，我直接自己把控命运

2.三数取中 左边 中间 右边 取不是最大,也不是最小的那个做Key

三数取中 完美的提高了性能（质量的提升）

就是快排面对最坏的情况（有序），选中位数做key，瞬间变成最好的情况

//三数取中
int GetMinIndex(int* a, int left, int right) {
	//这样可以防止 int 溢出
	int mid = left + (right - left) / 2;
	if (a[left] < a[mid]) {
		if (a[mid] < a[right])
			return mid;
		else if (a[left] > a[right])
			return left;
		else
			return right;
	}
	else //a[left] >= a[mid]
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[left] < a[right])
			return left;
		else
			return right;
	}
}

递归程序的缺陷

1.相比循环程序来说，性能有点差。（针对早期编译器，是这样的，因为对于递归调用，建立栈帧优化不大，而现在的编译器优化都很好，递归相比循环性能差不了多少）。所以现在这个不是核心矛盾

2.==核心矛盾是：==递归深度太深，会导致栈溢出

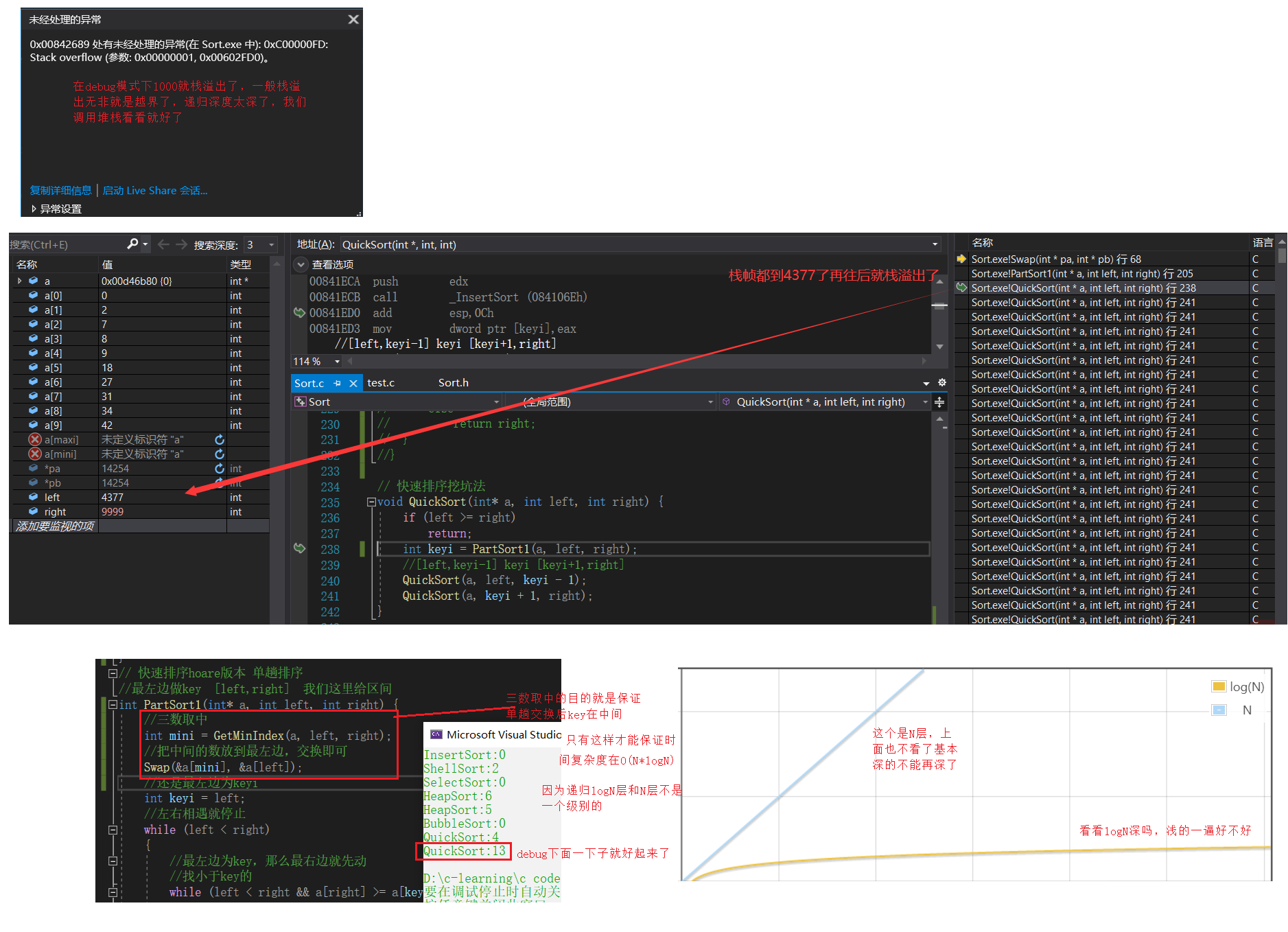
优化后的单趟排序

// 快速排序hoare版本 单趟排序
//最左边做key  [left,right]  我们这里给区间
int PartSort1(int* a, int left, int right) {
	//三数取中
	int mini = GetMinIndex(a, left, right);
	//把中间的数放到最左边，交换即可
	Swap(&a[mini], &a[left]);
	//还是最左边为keyi
	int keyi = left;
	//左右相遇就停止
	while (left < right)
	{
		//最左边为key，那么最右边就先动
		//找小于key的
		while (left < right && a[right] >= a[keyi]) {
			right--;
		}
		//然后再动右边的
		//找大于key的
		while (left < right && a[left] <= a[keyi]) {
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[right]);
	//返回正确位置后的keyi
	return left;
}

2.挖坑法

有人觉得hoare版本有点不好理解，单趟排序就想出了挖坑法

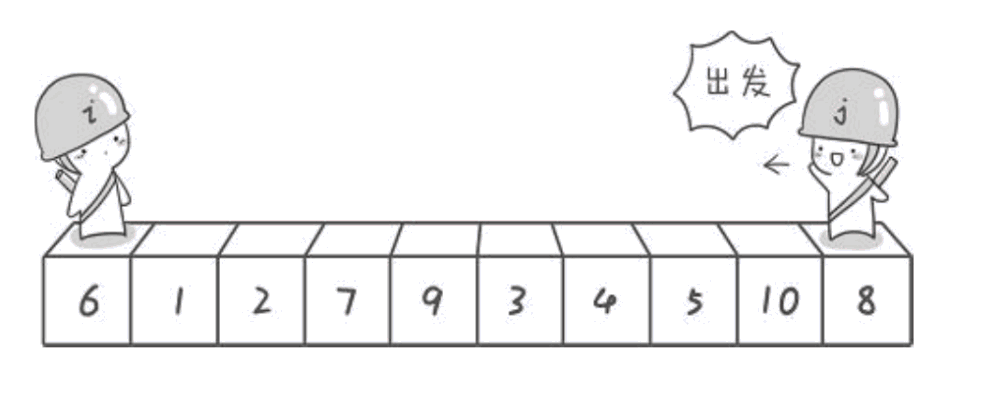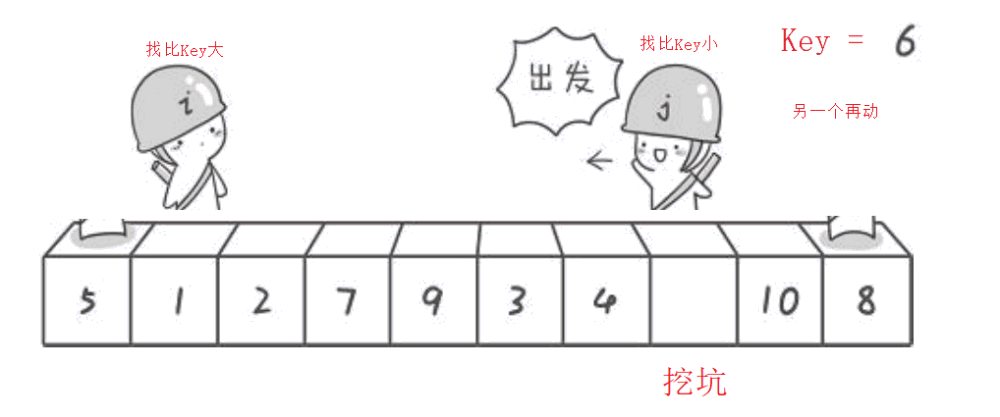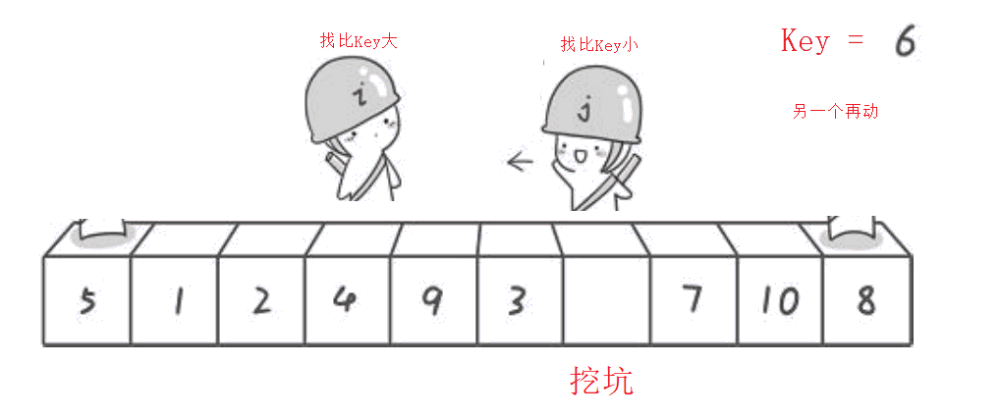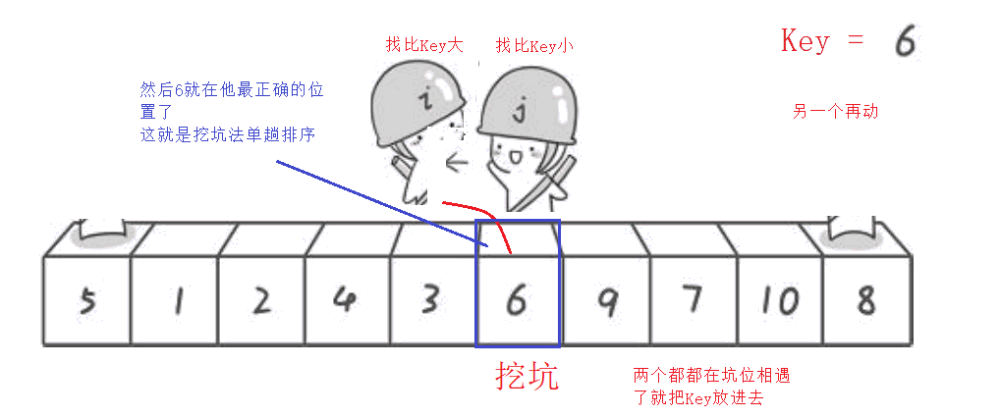
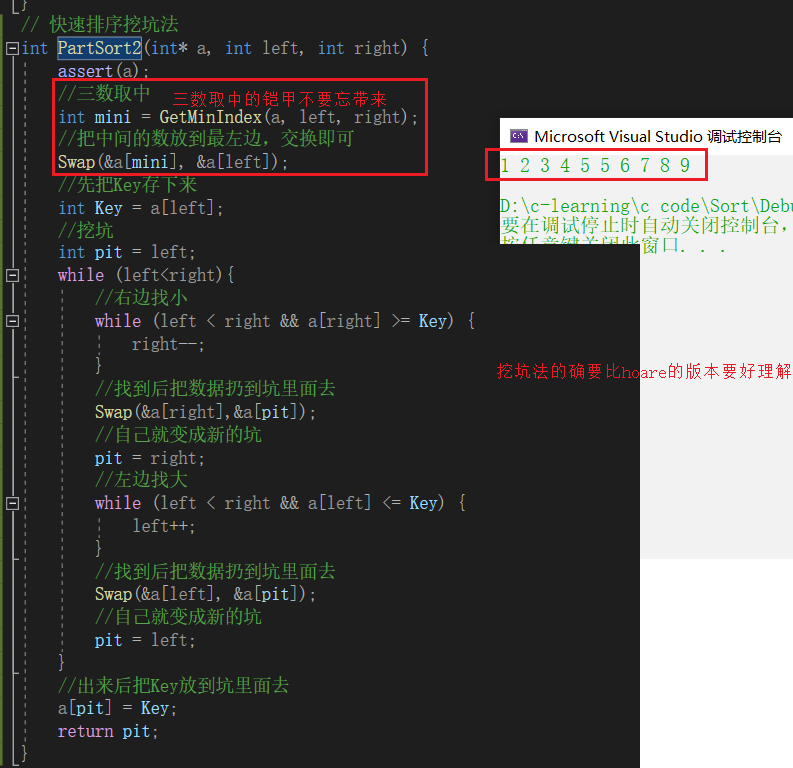
挖坑法的单趟排序

// 快速排序挖坑法
int PartSort2(int* a, int left, int right) {
	assert(a);
	//三数取中
	int mini = GetMinIndex(a, left, right);
	//把中间的数放到最左边，交换即可
	Swap(&a[mini], &a[left]);
	//先把Key存下来
	int Key = a[left];
	//挖坑
	int pit = left;
	while (left<right){
		//右边找小
		while (left < right && a[right] >= Key) {
			right--;
		}
		//找到后把数据扔到坑里面去
		Swap(&a[right],&a[pit]);
		//自己就变成新的坑
		pit = right;
		//左边找大
		while (left < right && a[left] <= Key) {
			left++;
		}
		//找到后把数据扔到坑里面去
		Swap(&a[left], &a[pit]);
		//自己就变成新的坑
		pit = left;
	}
	//出来后把Key放到坑里面去
	a[pit] = Key;
	return pit;
}

3.前后指针法

最左边为Key

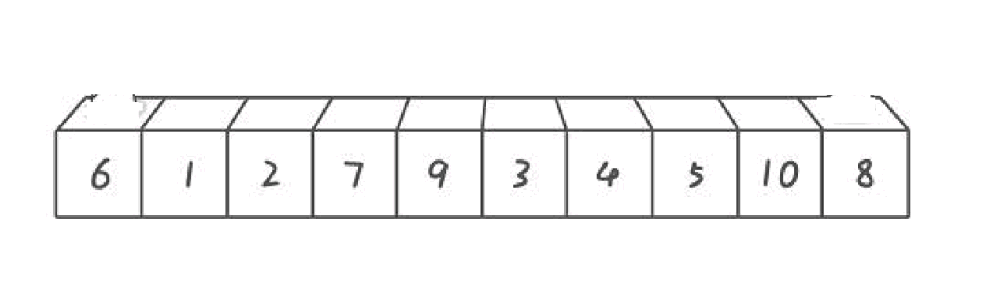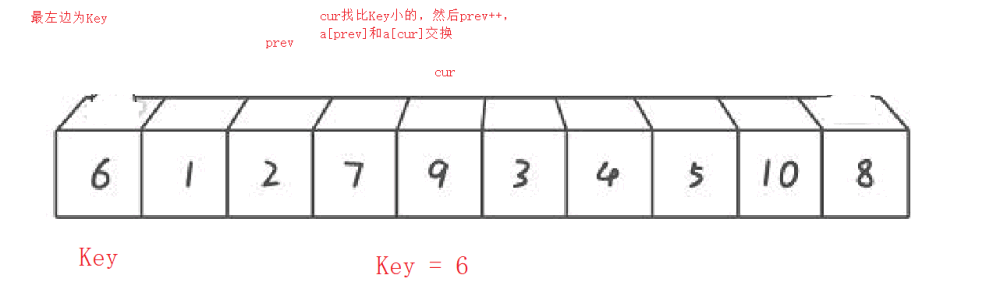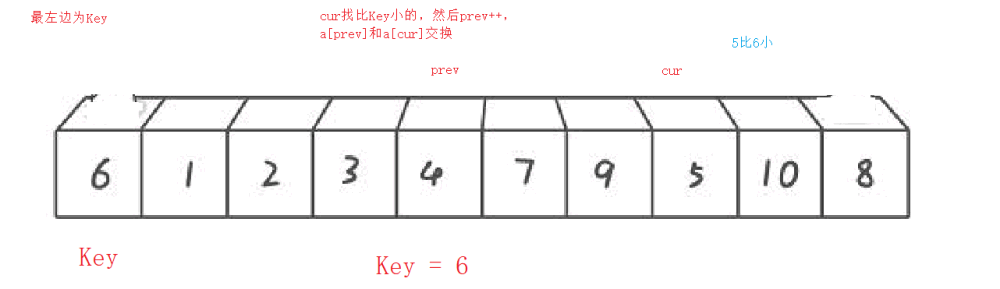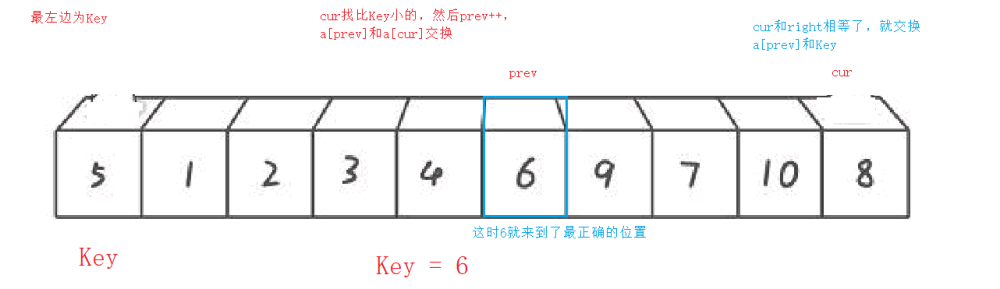
最右边为Key

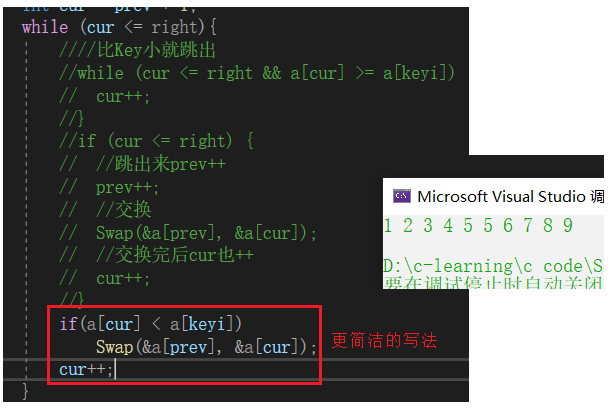
前后指针法的单趟排序 最左边为Key

// 快速排序前后指针法
int PartSort3(int* a, int left, int right) {
	assert(a);	
	//三数取中
	int mini = GetMinIndex(a, left, right);
	//把中间的数放到最左边，交换即可
	Swap(&a[mini], &a[left]);
	//把keyi记下来
	int keyi = left;
	int prev = left;
	int cur = prev + 1;
	while (cur <= right){
		比Key小就跳出
		//while (cur <= right && a[cur] >= a[keyi]) {
		//	cur++;
		//}
		//if (cur <= right) {
		//	//跳出来prev++
		//	prev++;
		//	//交换
		//	Swap(&a[prev], &a[cur]);
		//	//交换完后cur也++
		//	cur++;
		//}		
		if(a[cur] < a[keyi])
			Swap(&a[prev], &a[cur]);
		cur++;
	}
	//跳出来说明交换a[prev]和Key
	Swap(&a[prev],&a[keyi]);
	return prev;
}

实际上快排还是有缺陷的

比如还是特殊情况那种 一个数组都是一样的数字 假如是5

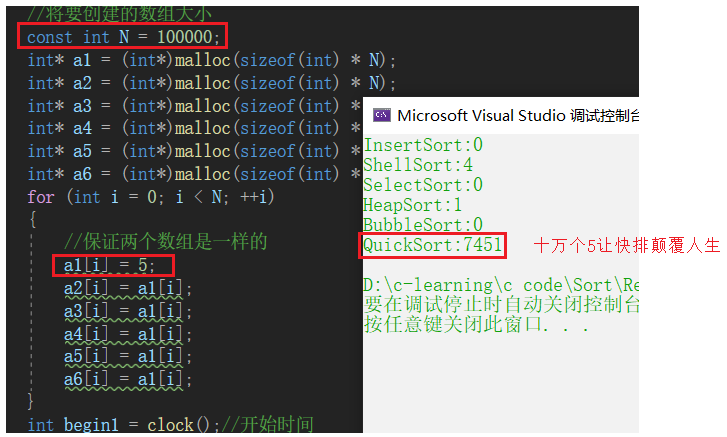
小区间优化

有时候会发现数据很小的时候用递归会有一种杀鸡用牛刀的感觉，所有我们小区间用插入来解决，(递归回来的小区间也是用插入来解决)

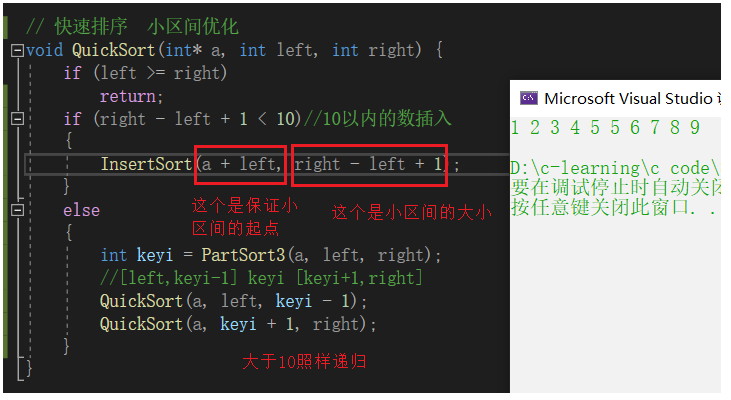
快速排序 小区间优化

// 快速排序  小区间优化
void QuickSort(int* a, int left, int right) {
	if (left >= right)
		return;
	if (right - left + 1 < 10)//10以内的数插入
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		int keyi = PartSort3(a, left, right);
		//[left,keyi-1] keyi [keyi+1,right]
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}	
}

快排的非递归

用栈保存区间，来代替递归

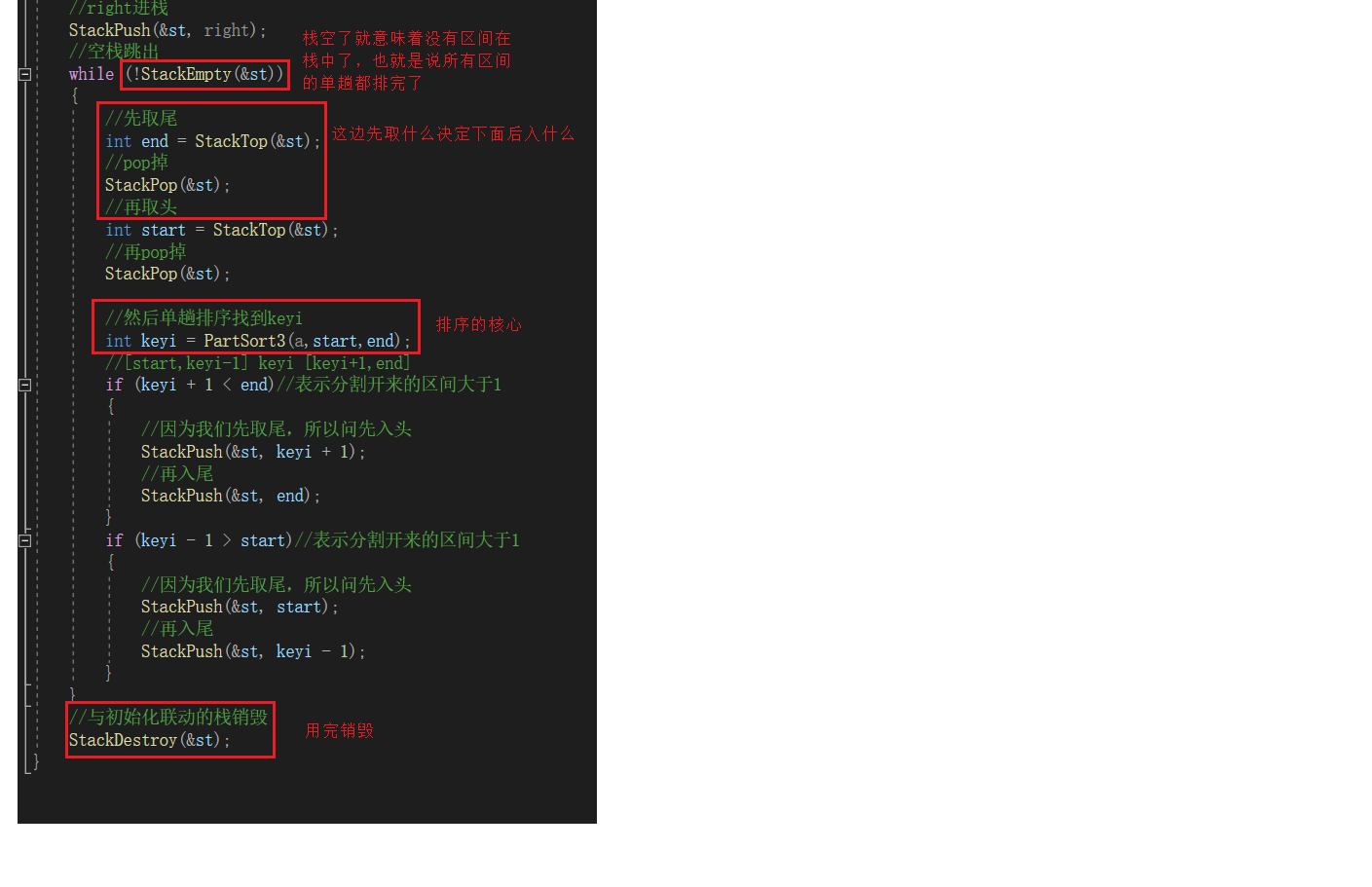
快排非递归写法

// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right) {
	//建栈
	ST st;
	//初始化栈
	StackInit(&st);
	//left进栈
	StackPush(&st, left);
	//right进栈
	StackPush(&st, right);
	//空栈跳出 
	while (!StackEmpty(&st))
	{
		//先取尾
		int end = StackTop(&st);
		//pop掉
		StackPop(&st);
		//再取头
		int start = StackTop(&st);
		//再pop掉
		StackPop(&st);

		//然后单趟排序找到keyi
		int keyi = PartSort3(a,start,end);
		//[start,keyi-1] keyi [keyi+1,end]
		if (keyi + 1 < end)//表示分割开来的区间大于1
		{
			//因为我们先取尾，所以问先入头
			StackPush(&st, keyi + 1);
			//再入尾
			StackPush(&st, end);
		}
		if (keyi - 1 > start)//表示分割开来的区间大于1
		{
			//因为我们先取尾，所以问先入头
			StackPush(&st, start);
			//再入尾
			StackPush(&st, keyi - 1);
		}
	}
	//与初始化联动的栈销毁
	StackDestroy(&st);
}

所有代码

Sort.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>

#define HEAP        1

// 排序实现的接口
// 打印数组
extern void PrintArray(int* a, int n);
// 插入排序
extern void InsertSort(int* a, int n);
// 希尔排序
extern void ShellSort(int* a, int n);
//数据交换
extern void Swap(int* pa, int* pb);
// 选择排序
extern void SelectSort(int* a, int n);
//向下调整
extern void AdjustDwon(int* a, int n, int parent);
// 堆排序
extern void HeapSort(int* a, int n);
// 冒泡排序
extern void BubbleSort(int* a, int n);
// 快速排序递归实现
// 快速排序hoare版本
extern int PartSort1(int* a, int left, int right);
// 快速排序挖坑法
extern int PartSort2(int* a, int left, int right);
// 快速排序前后指针法
extern int PartSort3(int* a, int left, int right);
extern void QuickSort(int* a, int left, int right);
// 快速排序 非递归实现
extern void QuickSortNonR(int* a, int left, int right);
// 归并排序递归实现
extern void MergeSort(int* a, int n);
// 归并排序非递归实现
extern void MergeSortNonR(int* a, int n);
// 计数排序
extern void CountSort(int* a, int n);

Sort.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "Sort.h"
#include"Stack.h"

// 打印数组
void PrintArray(int* a, int n) {
	assert(a);
	int i = 0;
	for (i = 0; i < n; i++) {
		printf("%d ", a[i]);
	}
	printf("\n");
}
// 插入排序
void InsertSort(int* a, int n) {
	assert(a);
	int i = 0;
	for (i = 0; i < n - 1; i++)	{
		int end = i;
		int x = a[end+1];
		while (end >= 0) {
			//要插入的数比顺序中的数小就准备挪位置
			if (a[end] > x) {
				a[end + 1] = a[end];
				end--;
			}
			else {
				//插入的数比顺序中的要大就跳出
				break;
			}
		}
		//跳出来两种情况
		//1.end == -1 的时候
		//2.break 的时候
		//把x给end前面一位
		a[end + 1] = x;
	}
}
// 希尔排序
void ShellSort(int* a, int n) {
	//分组
	int gap = n;
	//多次预排序（gap>1）+ 直接插入（gap == 1）
	while (gap>1){
		//gap /= 2;
		//除以三我们知道不一定会过1，所以我们+1让他有一个必过1的条件
		gap = gap / 3 + 1;
		//单组多躺
		int i = 0;
		for (i = 0; i < n - gap; i++) {
		int end = i;
		int x = a[end + gap];
		while (end >= 0) {
			if (a[end] > x) {
				a[end + gap] = a[end];
				//步长是gap
				end -= gap;
			}
			else {
				break;
			}
		}
		a[end + gap] = x;
	}
	}	
}
//数据交换
void Swap(int* pa, int* pb) {
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
// 选择排序
void SelectSort(int* a, int n) {
	int begin = 0;
	int end = n - 1;
	while (begin < end){
		//单趟
		//最大数，最小数的下标
		int mini = begin;//这边假设是刚开始的下标
		int maxi = end;  //这边假设是末尾的下标
		int i = 0;
		for (i = begin; i <= end; i++) {
			if (a[i] < a[mini])
				mini = i;
			if (a[i] > a[maxi])
				maxi = i;
		}
		//最小的放前面
		Swap(&a[begin], &a[mini]);
		
		if (begin == maxi)
			//如果最大数就是begin位置的，那么交换的时候最大数连带着下标一起动
			maxi = mini;
		//最大的放后面
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}
//向下调整函数
void AdjustDown(int* a, int n, int parent)
{
	assert(a);
	//创建一个孩子变量，有两个孩子就在这个上加1就行
	int child = parent * 2 + 1;
#if HEAP
	while (child < n)
	{
		//选大孩子
		if (child + 1 < n && a[child] < a[child + 1])
		{
			child++;
		}
		//大的孩子还大于父亲就交换
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
#elif !HEAP
	while (child < n)
	{
		//选小孩子
		if (child + 1 < n && a[child] > a[child + 1])
		{
			child++;
		}
		//小的孩子还小于父亲就交换
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
#endif // HEAP	
}
// 堆排序   我们之前讲过升序建大堆
void HeapSort(int* a, int n) {
	//建堆时间复杂度O(N)
	//建大堆
	int i = 0;
	for (i = (n - 1 - 1) / 2; i >= 0; i--) {
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	//堆排序时间复杂度O(N*logN)
	while (end>0){
		//交换 把最大的放到后面
		Swap(&a[0], &a[end]);
		//在向下调整
		AdjustDown(a,end,0);
		end--;
	}
}
// 冒泡排序
void BubbleSort(int* a, int n) {
	//多躺
	int j = 0;	
	for (j = 0; j < n - 1; j++) {	
		//交换标记变量
		int flag = 0;
		//单趟
		int i = 0;
		for (i = 0; i < n - 1-j; i++) {
			//交换标记改变
			flag = 1;
			if (a[i] > a[i + 1]) {
				Swap(&a[i], &a[i + 1]);
			}
		}
		//标记还是0就跳出
		if (!flag)
			break;
	}
}
//三数取中
int GetMinIndex(int* a, int left, int right) {
	//这样可以防止 int 溢出
	int mid = left + (right - left) / 2;
	if (a[left] < a[mid]) {
		if (a[mid] < a[right])
			return mid;
		else if (a[left] > a[right])
			return left;
		else
			return right;
	}
	else //a[left] >= a[mid]
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[left] < a[right])
			return left;
		else
			return right;
	}
}
// 快速排序hoare版本 单趟排序
//最左边做key  [left,right]  我们这里给区间
int PartSort1(int* a, int left, int right) {
	//三数取中
	int mini = GetMinIndex(a, left, right);
	//把中间的数放到最左边，交换即可
	Swap(&a[mini], &a[left]);
	//还是最左边为keyi
	int keyi = left;
	//左右相遇就停止
	while (left < right)
	{
		//最左边为key，那么最右边就先动
		//找小于key的
		while (left < right && a[right] >= a[keyi]) {
			right--;
		}
		//然后再动右边的
		//找大于key的
		while (left < right && a[left] <= a[keyi]) {
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[right]);
	//返回正确位置后的keyi
	return left;
}
// 快速排序挖坑法
int PartSort2(int* a, int left, int right) {
	assert(a);
	//三数取中
	int mini = GetMinIndex(a, left, right);
	//把中间的数放到最左边，交换即可
	Swap(&a[mini], &a[left]);
	//先把Key存下来
	int Key = a[left];
	//挖坑
	int pit = left;
	while (left<right){
		//右边找小
		while (left < right && a[right] >= Key) {
			right--;
		}
		//找到后把数据扔到坑里面去
		Swap(&a[right],&a[pit]);
		//自己就变成新的坑
		pit = right;
		//左边找大
		while (left < right && a[left] <= Key) {
			left++;
		}
		//找到后把数据扔到坑里面去
		Swap(&a[left], &a[pit]);
		//自己就变成新的坑
		pit = left;
	}
	//出来后把Key放到坑里面去
	a[pit] = Key;
	return pit;
}

// 快速排序前后指针法
int PartSort3(int* a, int left, int right) {
	assert(a);	
	//三数取中
	int mini = GetMinIndex(a, left, right);
	//把中间的数放到最左边，交换即可
	Swap(&a[mini], &a[left]);
	//把keyi记下来
	int keyi = left;
	int prev = left;
	int cur = prev + 1;
	while (cur <= right){
		比Key小就跳出
		//while (cur <= right && a[cur] >= a[keyi]) {
		//	cur++;
		//}
		//if (cur <= right) {
		//	//跳出来prev++
		//	prev++;
		//	//交换
		//	Swap(&a[prev], &a[cur]);
		//	//交换完后cur也++
		//	cur++;
		//}		
		if(a[cur] < a[keyi])
			Swap(&a[prev], &a[cur]);
		cur++;
	}
	//跳出来说明交换a[prev]和Key
	Swap(&a[prev],&a[keyi]);
	return prev;
}


// 快速排序  小区间优化
void QuickSort(int* a, int left, int right) {
	if (left >= right)
		return;
	if (right - left + 1 < 10)//10以内的数插入
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		int keyi = PartSort3(a, left, right);
		//[left,keyi-1] keyi [keyi+1,right]
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}	
}
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right) {
	//建栈
	ST st;
	//初始化栈
	StackInit(&st);
	//left进栈
	StackPush(&st, left);
	//right进栈
	StackPush(&st, right);
	//空栈跳出 
	while (!StackEmpty(&st))
	{
		//先取尾
		int end = StackTop(&st);
		//pop掉
		StackPop(&st);
		//再取头
		int start = StackTop(&st);
		//再pop掉
		StackPop(&st);

		//然后单趟排序找到keyi
		int keyi = PartSort3(a,start,end);
		//[start,keyi-1] keyi [keyi+1,end]
		if (keyi + 1 < end)//表示分割开来的区间大于1
		{
			//因为我们先取尾，所以问先入头
			StackPush(&st, keyi + 1);
			//再入尾
			StackPush(&st, end);
		}
		if (keyi - 1 > start)//表示分割开来的区间大于1
		{
			//因为我们先取尾，所以问先入头
			StackPush(&st, start);
			//再入尾
			StackPush(&st, keyi - 1);
		}
	}
	//与初始化联动的栈销毁
	StackDestroy(&st);
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "Sort.h"

// 测试排序的性能对比
void TestOP()
{
	//设置随机起点
	srand(time(NULL));
	//将要创建的数组大小
	const int N = 10000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		//保证两个数组是一样的
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
	}
	int begin1 = clock();//开始时间
	//InsertSort(a1, N);
	int end1 = clock();  //结束时间
	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();
	int begin3 = clock();
	//SelectSort(a3, N);
	int end3 = clock();
	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();
	int begin4_1 = clock();
	HeapSort(a2, N);
	int end4_1 = clock();
	int begin5 = clock();
	//BubbleSort(a5, N);
	int end5 = clock();
	int begin6 = clock();
	QuickSort(a6, 0, N - 1);
	int end6 = clock();
	int begin6_1 = clock();
	QuickSort(a2,0,N-1);
	int end6_1 = clock();
	printf("InsertSort:%d\n", end1 - begin1);//结束时间减去开始时间 
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("HeapSort:%d\n", end4_1 - begin4_1);
	printf("BubbleSort:%d\n", end5 - begin5);
	printf("QuickSort:%d\n", end6 - begin6);
	printf("QuickSort:%d\n", end6_1 - begin6_1);
	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
}
//测试插入排序
void TestInsertSort() {
	int a[] = { 1,5,3,7,0,9 };
	InsertSort(a, sizeof(a) / sizeof(a[0]));	
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试希尔排序
void TestShellSort() {
	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
	ShellSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试选择排序
void TestSelectSort() {
	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
	SelectSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试堆排序
void TestHeapSort() {
	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
	HeapSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试冒泡排序
void TestBubbleSort() {
	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
	BubbleSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试单趟排序
void TestPartSort1() {
	int a[] = { 5,5,5,5,5,5,5,5,5,5 };
	PartSort1(a,0 ,sizeof(a) / sizeof(a[0])-1);
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试快速排序
void TestQuickSort() {
	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
	QuickSort(a, 0, sizeof(a) / sizeof(a[0]) - 1);
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试快速排序--非递归
void TestQuickSortNonR() {
	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
	QuickSortNonR(a, 0, sizeof(a) / sizeof(a[0]) - 1);
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main(){
	//TestInsertSort();
	//TestShellSort();
	//TestSelectSort();
	//TestHeapSort();
	//TestBubbleSort();
	//TestPartSort1();
	//TestQuickSort();
	TestQuickSortNonR();
	//TestOP();
	return 0;
}