数据结构——线性表
- 🔔前言:为学日进,为道日损。与诸君携手共勉 💖💖💖
- 💓线性表的基本概念
- 🌟线性表的定义
- 🌟线性表的基本操作
- 💓线性表的顺序存储
- ✅顺序表
- ✅顺序表基本运算的实现
- 🌟顺序表类型定义
- 🌟顺序表的初始化
- 🌟顺序表的建立
- 🌟查找操作
- 🌻按位置查找
- 🌻按值查找
- 🌟插入操作
- 🌟删除操作
- 🌟输出顺序表中数据
- 💓线性表的链式存储
- ✅单链表
- ✅单链表的基本操作实现
- 🌟单链表类型定义
- 🌟单链表的初始化
- 🌟单链表的建立
- 🌟获得单链表的表长
- 🌟查找操作
- 🌟插入操作
- 🌟删除操作
- 🌟输出操作
- 💓总结——顺序表和链表的比较
- 🔔写在最后🎈🎈🎈
- 拙文一曲,若有偏僻,欢迎及时雅正( ^ - ^ )
- 持续更新对数据结构的总结和理解喔💖💖💖
🔔前言:为学日进,为道日损。与诸君携手共勉 💖💖💖

💓线性表的基本概念
🌟线性表的定义
定义:
线性表是零个或多个(n >= 0)具有相同数据类型的数据元素的有限序列.
通常记作:(a1,a2,…,ai-1,ai,ai+1,…,an)。n是表长,n = 0的线性表被称为空表
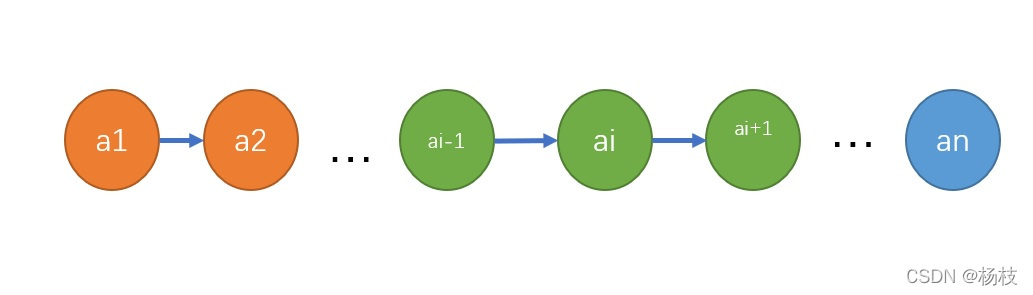
举个栗子

特点:
在线性表中相邻元素之间存在顺序关系。即,对于元素ai而言,ai-1称为ai的直接前驱,ai+1称为ai的直接后继。
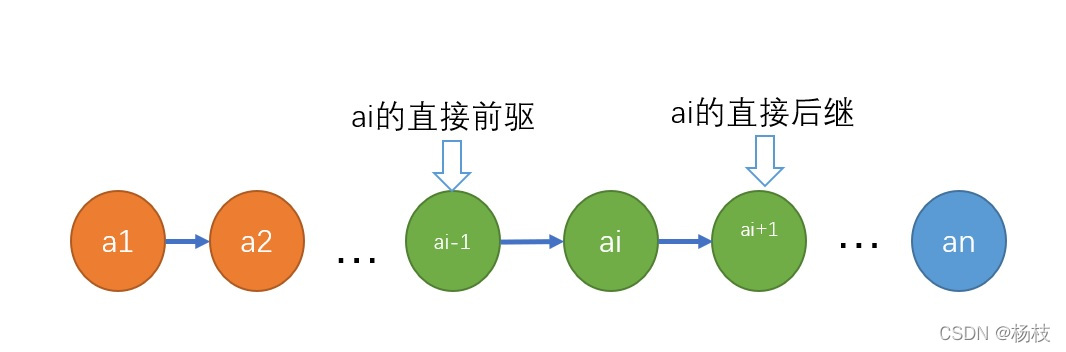
故,除了开始结点(a1)和终端结点(an)以外,其余所有结点都有且仅有一个直接前驱和一个直接后继
🌟线性表的基本操作
- 初始化线性表InitList(L)
- 求线性表长度GetLength(L)
- 按位置查找操作GetElem(L,i,x)
- 按值查找操作Locate(L,x)
- 插入操作InsElem(L,i,x)
- 删除操作DelElem(L,i,x)
- 显示操作DispList(L)
好多喔✊✊✊

进入下一个模块喽~⏩
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
💓线性表的顺序存储
✅顺序表
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表中的数据元素
简单来说,线性表的顺序存储结构就是在内存中找一块地儿,把它占了,然后把相同数据类型的数据元素依次存放在这块空地中,所以可以直接用一个一维数组实现线性表的顺序存储结构

✅顺序表基本运算的实现
🌟顺序表类型定义
#define MAXLEN 100 //定义常量MAXLEN = 100用于表示存储空间的总量
typedef int DataType; //定义DataType为int型
typedef struct{ //顺序表存储类型
DataType data[MAXLEN]; //存放线性表的数组
int Length; //Length表示当前线性表的中长度
}SeqList;
SeqList L; //定义一个顺序表,名字是L,同时它也是全局变量
顺序表SeqList是一个结构体类型,它由两个成员组成:data表示存储数据的数据和表示线性表当前实际的长度的Length
🌟顺序表的初始化
初始化也就把线性表回到最初表长是0的状态,通过将记录线性表实际长度的Length置为0实现
void InitList(SeqList *L)
{
L->Length = 0; //初始化顺序表为空
}
🌟顺序表的建立
从键盘录入n个数据,并将这些数据存入到顺序表中,修改表长
void CreateList(SeqList *L,int n)
{
int i;
printf("请输入%d个整数:",n) ;
for(i = 0; i < n;i++)
scanf("%d",&L->data[i]);
L->Length = i; //更新表长
}
🌟查找操作
注意:顺序表中的位置是从1开始计数的,联系到日常生活中,说的是第1个位置,第2个位置,也没有说第0个位置的说法吧~。
但是用来记录顺序表的数组是0开始计数的

🌻按位置查找
查找顺序表中第i个位置元素的值,在i无效时返回出错,有效是返回成功,并用指针x所指向的变量传回第i个元素的值
int GetElem(SeqList *L,int i,DataType *x)
{
//异常处理
if(i < 1 || i >L->Length) return 0;
else
{
*x = L->data[i-1];//顺序表中的位置是从1开始计算的
return 1;
}
}
🌻按值查找
在顺序表中查找与给定的x相等的数据元素的位置的所在位置。
int Locate(SeqList *L,DataType x)
{
int i = 0;
while(i < L->Length && L->data[i] != x) i++;
if(i >= L->Length) return 0;
else return i+1;
}
🌟插入操作

实现思路:
- 特判。当插入的位置不合理了,抛出异常
- 将ai~an之间的所有结点依次后移,为新元素让出第i个位置
- 将新结点x插入到第i个位置
- 修改表长
参考实现代码:
int InsElem(SeqList *L,int i,DataType x)
{
int j;
//异常处理
//表满了,不能插入了
if(L->Length >= MAXLEN)
{
printf("顺序表已满,无法插入");
return -1;
}
//提供的插入位置不合法
if(i < 1 || i > L->Length+1)
{
printf("插入位置出错,无法插入");
return 0;
}
//插入位置在表尾,直接插入即可
if(i == L->Length+1)
{
L->data[i-1] = x;
L->Length++;
return 1;
}
//插入到表中某个位置,则插入点后各个结点后移。
//可以取巧从末尾开始移动,那么每次都只用移动一位,不用每次都移动n-i位
for(j = L->Length-1;j >= i-1;j--)
{
L->data[j+1] = L->data[j];
L->data[i-1] = x;
L->Length ++;
return 1;
}
}
🌟删除操作

实现思路:
- 将要删除的元素值,赋值给指针x所指的变量,需要这数据时就可以及时获得
- 将ai+1~an之间的结点依次向前移动
- 顺序表长度减1
参考实现代码:
int DelElem(SeqList *L,int i,DataType *x)
{
int j;
// 异常处理
//顺序表为空
if(L->Length == 0)
{
printf("顺序表为空,无法删除");
return 0;
}
//给定删除位置不合法
if(i < 1 ||i > L->Length)
{
printf("不存在第i个元素");
return 0;
}
*x = L->data[i-1];// 用指针变量*x存储删除元素的值,用于返回
//移动数组,覆盖要删除的元素
for(j = i; j < L->Length;j++) L->data[j-1] = L->data[j];
//更新线性表长度
L->Length--;
return 1;
}
🌟输出顺序表中数据
因为顺序表本质是数组,所以输出数据就是简单遍历数组就可以啦~
void DispList(SeqList *L)
{
int i = 0;
for(i =0;i< L->Length;i++) printf("%d ",L->data[i]);
}

好了。进入下一个模块啦~⏩
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
💓线性表的链式存储
✅单链表
顺序表结构简单,在访问表中元素的时候也特别方便,只要O(1)的时间复杂度,但是当数据规模十分庞大的时候,使用顺序表完成插入和删除操作就需要移动大量元素了。
此外,由于顺序表的空间是需要提前规定好了,再在内存中开辟相应的空间大小出来,因此容易出现空间估计过大造成内存浪费和空间估计过小导致溢出。因此引入了链式存储结构,它不需要用地址连续的存储单元实现,通过指针构建"链"建立元素之间的逻辑

单链表定义:

线性表的链式存储结构是指用一组任意的存储单元(可以连续,也可以不连续)存储线性表中的数据元素。为了反映数据元素之间的逻辑关系,对于每个数据元素不仅要表示它的具体内容,还要附加一个表示它的直接后继元素存储位置信息,这样构成的链表称为线性单向链接表,简称单链表。

小知识点

-
单链表一般是分为带头结点和不带头结点的,它们本质是一样的,带和不带都是正确的,只是因为带了头结点可以使对单链表的操作更统一,所以大多数人习惯带上头结点。
-
头指针和头结点。头指针是链表第一个结点的地址,头指针是必须的。通过头指针中的地址获得了第一个结点以后,才能对其他数据元素实现操作。头结点是人们为了统一操作而加上的,不是必须的。举个栗子,倘若不带头结点,删除第一个结点的算法是需要额外构建的。

✅单链表的基本操作实现
🌟单链表类型定义
typedef int DataType; //定义DataType 为int 类型
typedef struct linknode{ //单链表存储类型
DataType data; //数据域
struct linknode *next; //指针域
}LinkList;
上面代码中:
LinkList 是一个标识符,说直白一点了,它就是一个名字,它的类型是linknode类型。
如果想定义指向该类型的指针head:
LinkList *head;
如果想动态申请一个结点空间,并让指针head指向该结点空间:
head = (LinkList*)malloc(sizeof(struct linknode));//malloc函数:如果分配成功则返回指向被分配内存的指针,否则返回空指针NULL。
此时这个结点的数据域就是head ->data(也可以表达为(*head).data);这个结点的指针域就是head->next(也可以表达为(*head).next)
释放动态申请的空间
free(head);

🌟单链表的初始化
首先申请一个结点并让指针head指向该结点。
然后让指针head指向该结点,并将它的指针域赋值为空(NULL)
最后返回头指针head.
LinkList *InitList()
{
LinkList *head;
head=(LinkList*)malloc(sizeof(LinkList)); //动态分配一个结点空间
head->next=NULL;
return head; //此时头结点的指针域为空,表示空链表
}
🌟单链表的建立
头插法建表
建立线性表从空表开始。每次读入有效的数据就申请一个结点s,
将读取的数据放到新结点s的数据域中,
然后将新结点接在当前链表head的表头后面

参考实现代码:
void CreateListH(LinkList *head,int n)
{
LinkList *s;
int i;
printf("请输入%d个整数:",n);
for(i=0;i<n;i++)
{
s=(LinkList *)malloc(sizeof(LinkList));
scanf("%d",&s->data);
s->next=head->next;
head->next=s;
}
printf("建立链表操作成功");
}
尾插法建表
因为头插法是将数据挨着挨着插入到开头,所以最后得到的序列是和输入次序相反的。尾插法则可实现次序一致。
实现流程:
每读入一个有效数据就申请一个结点s,并将读取的数据存放到新结点s的指针域,
将s的尾指针设置为空(NULL)
将新结点插入到当前链表的尾部(尾指针last所指的结点后面)

参考实现代码:
void CreateListL(LinkList *head,int n)
{
LinkList *s,*last;
int i;
last=head;
printf("请输入%d个整数:",n);
for(i=0;i<n;i++)
{
s=(LinkList *)malloc(sizeof(LinkList));
scanf("%d",&s->data);
s->next=NULL;
last->next=s;
last=s;
}
printf("建立链表操作成功!");
}
🌟获得单链表的表长
从头指针的位置开始遍历,同时放置一个计数器用来记录遍历了多少个结点。最后计数器的数值就是链表的长度
参考实现代码:
int LengthList(LinkList *head)
{
LinkList *p=head->next;
int cnt=0;//计数器
while(p!=NULL)
{
p=p->next;
cnt++;
}
return cnt;
}

🌟查找操作
思路和顺序表的查找是一致的,换汤不换药,就不在赘述流程啦~
依旧有按值查找和按位置查找
按值查找参考代码:
//按值查找
void Locate(LinkList *head,DataType x)
{
int j=1;
LinkList *p;
p=head->next;
while(p!=NULL&&p->data!=x)
{
p=p->next;
j++;
}
if(p!=NULL)
printf("在表中的第%d位找到值为%d的结点",j,x);
else
printf("未找到值为%d的结点",x);
}
按序号/位置查找参考代码
void SearchList(LinkList *head,int i)
{
LinkList *p;
int j=0;
p=head;
if(i>LengthList(head))
printf("位置错误,链表中没有该位置");
while(p->next!=NULL&&j<i)
{
p=p->next;
j++;
}
if(j==i)
printf("在第%d位上的元素为%d",i,p->data);
}
🌟插入操作
倘若要在指针p所指的结点后面插入一个结点,
实现思想
①先将结点s的指针域指向结点p的指针域所指向的位置(s->next = p->next)
②再将结点p的指针域指向新结点s(p->next = s)

注意:语句①和语句②不能颠倒。

插入操作参考代码
void InsList(LinkList *head,int i,DataType x)
{
//按位置插入
int j=0;
LinkList *p,*s;
p=head;
while(p->next!=NULL&&j<i-1) //定位插入的位置
{
p=p->next;
j++;
}
if(p!=NULL) //p不为空则将新结点插到p后面
{
s=(LinkList *)malloc(sizeof(LinkList));
s->data=x;
s->next=p->next;
p->next=s;
printf("插入元素成功");
}
else
printf("插入元素失败");
}
🌟删除操作
实现思想
①通过循环定位出第i个结点的直接前驱(即第i-1个结点)p的地址
②然后将指针s指向要被删除的结点
③修改p->next指针,使其指向s后的结点,释放指针s所指向的结点
注意if(p->next!=NULL&&j==i-1)。只有当第i-1个结点存在(j == i-1) 并且 p不是终点结点(p->next != NULL)时 ,才能确实被删除的结点存在。

参考实现代码:
void DelList(LinkList *head,int i)
{
int j=0;
DataType x;
LinkList *p=head,*s;
while(p->next!=NULL&&j<i-1)
{
p=p->next;
j++;
}
if(p->next!=NULL&&j==i-1)
{
s=p->next; //s指向要被删除的结点
x=s->data; //将要删除的数据放入指针变量x中
p->next=s->next; //将p指针所指向的结点的指针域与s指针所指向的结点的后一个结点建立联系
free(s);
printf("删除第%d位上的元素%d成功",i,x);
}
else
printf("删除结点位置错误,删除失败");
}
🌟输出操作
获取头指针中存放的第一个结点的地址,开始逐一遍历输出各个结点中的数据就可以了

参考实现代码:
void DisList(LinkList *head)
{
LinkList *p;
p=head->next;
while(p!=NULL)
{
printf("%5d",p->data);
p=p->next;
}
}
对于循环链表和双向链表,它俩除了会在考场上出现,其他地方几乎没有它的勇武之地。把玩会了单链表,再回眸它们,应该会是满脑子——就这。

完工喽~⏩
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
💓总结——顺序表和链表的比较
顺序表本质是数组,所以实现起来容易,逻辑也简单,查询直接把索引扔到数组里就像,插入和删除也只用移动数组。但是要提前估计使用的数据的规模,因为数组开辟出来以后就不能再改变了(可以扩容,但是很麻烦),而且当数据过于庞大的时候,插入和删除操作效率很低
因为链表实现逻辑主要依靠指针,就显得就复杂了很多,它查询的效率没有顺序表高,但是执行插入和删除时候比顺序表香。
可以看出来,顺序表的优点就是链表的缺点,而其缺点就是链表的优点。在算法竞赛中,就几乎使用她俩的结合版:静态链表
有兴趣的小伙伴可以看一下喔~ ,笔芯
数据结构——静态链表
🔔写在最后🎈🎈🎈
拙文一曲,若有偏僻,欢迎及时雅正( ^ - ^ )
持续更新对数据结构的总结和理解喔💖💖💖
