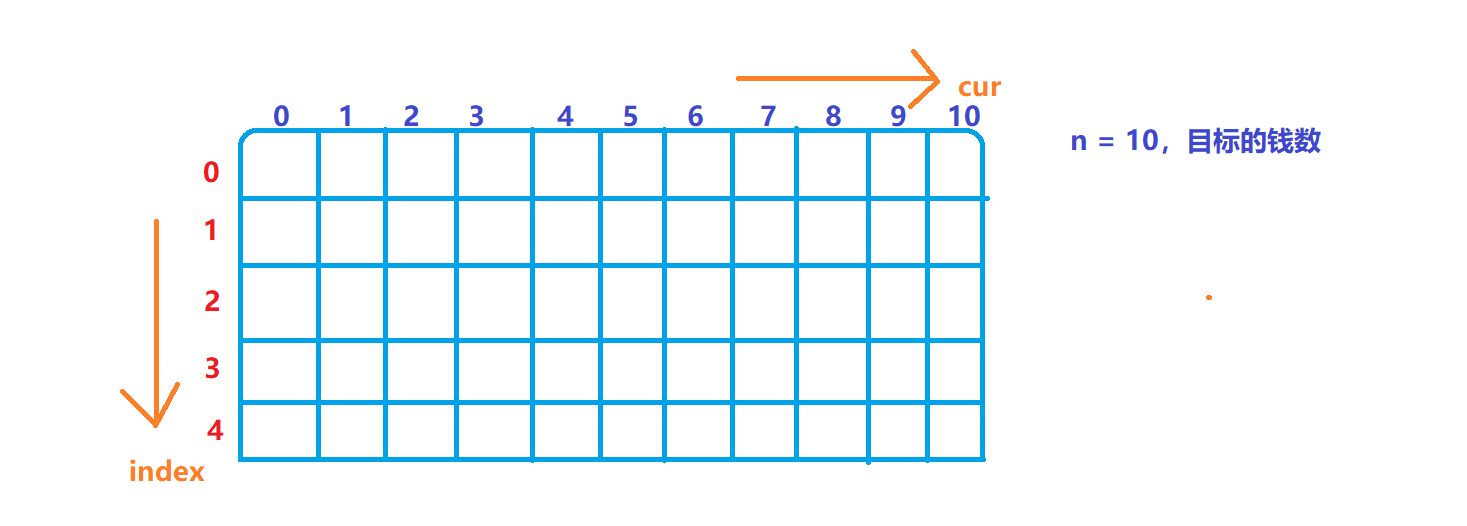
今天来看一道关于动态规划的算法题：硬币划分问题。LeetCode链接

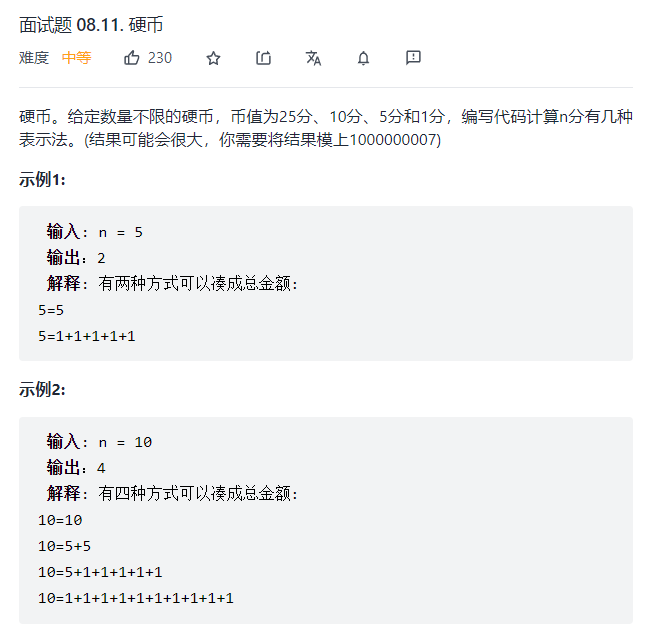
简单点说，就是给你一些硬币，这些硬币有很多个，现在问你，组成n分钱，可以有多少种组合方式。

一、暴力递归进行尝试解法

可能很多的人，拿到这道题，都不知道该如何进行下手，没有任何的思路。我也是一样的，只能先尝试着用暴力的方法，去写尝试的方法。

既然有一些硬币，那么我们就先用一个数组，将所有硬币的面值存储起来，切记，这里有一个潜规则：硬币在数组中的顺序，一定是按大小顺序进行排序的，要么是升序，要么是降序。

int[] coins = {1, 5, 10, 25}; //升序排列

然后就是我们要知道一个情况就是：假设n=10，硬币的组合方式有一种是1+1+1+1+1+5，这样一种方式，其实等价于这样：1+5+1+1+1+1。这两种，实则指的就是一种情况。根据这个情况，我们可以很明显的发现一个问题，那就是在使用硬币的时候，相同的硬币最好是在一起使用，也就是说不要出现上面一个5，将1分割成了两部分，如下图：

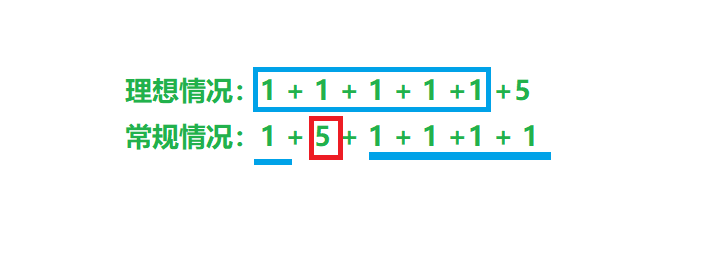
那要做到上图的理想情况，那就是在使用一种硬币的时候，保证一次性拿够（数量）。

在面对每一种硬币时，也就是在coins[i]时，当前这个位置的硬币，我可以选择要和不要两种情况。

所以根据上面分析，我们能够得出一个暴力递归的解法。

//递归尝试
public static int moneyCombine(int n) {
    if (n < 0) {
        return 0;
    }
    int[] coins = {1, 2, 5, 10}; //硬币的面值
    return process(coins, n, 0, 0);
}

/**
 * 暴力递归解法
 * @param coins 硬币面值
 * @param n     目标的钱数
 * @param cur   当前的钱数
 * @param index 硬币的下标值，潜规则，必须先把一种硬币使用完才能只用下一种硬币。
 * @return 返回最终的方法数
 */
public static int process(int[] coins, int n, int cur, int index) {
    if (cur == n) { //cur刚好等于n了，所以这是一种组合方式
        return 1;
    }
    if (cur > n || index == coins.length) {
        return 0;
    }
    int res = 0;
    res += process(coins, n, cur, index + 1); //当前位置的钱，我不想要
    //假设我要当前index位置的硬币
    //那么我可能要1个，要2个，又或者3个。没限制的话，只能一个个尝试
    //直到cur的超过n了，就停止当前位置硬币的尝试
    for (int i = cur + coins[index]; i <= n; i += coins[index]) {
        res += process(coins, n, i, index + 1); //当前位置的钱，我要了
    }
    return res;
}

以上就是递归的版本，核心就在于，相对于每一种硬币来说，我可以选择不要，又或者是要1个，或者是2个……，以这样的方式，一个一个的去尝试，这非常的暴力。

递归版本的代码，可能会出现大量的重复计算，因此就出现了动态规划。动态规划的本质就是在给递归做优化，把可能会进行重复计算的数值，保存到一张表中，下次需要这种状态的值的时候，直接从表里面拿取即可。

二、经典的dp解法

我们可以根据递归的版本，进行添加缓存，来达到一个优化。

在读递归版本的代码时，我们会发现，整个递归函数，只有两个可变参数，一个可变参数是cur，另一个可变参数是index。

这里记住一点，递归代码有几个可变参数，那么在设计dp表时，就需要几维表。此时可变参数是2个，那么我们建立一张二维数组，就能存储下所有的结果。（注：dp表不一定就是数组，有可能也会是map、set，得看题意）

这样的话，我们设计纵向（行数）的值就是index，横向（列数）的值就是cur。有如下图：

纵向：有多少种硬币，就开辟多长。

横向：n有多长，就开辟多长。

但是因为第一行和第一列是额外的，不包含在cur和index中，其实在开辟dp表时，需要额外的开辟一个单位空间，

实则就是new int【index+ 1】【n + 1】。

因为在递归版本的代码中，第一次调用递归函数的cur=0，index=0。所以在动态规划的代码中，我们需要返回dp【0】【0】的数值，这就是最终的答案。

因为返回dp表左上角的值，那么dp表肯定就是从下往上填写的。

//对于这道题来说，只有4种硬币，行数就开辟5行即可
int[][] dp = new int[5][n + 1];

现在dp表建好之后，就是如何进行填写这张表？？？

非常简单，递归版本的代码是怎么写的，dp表就该怎么填写。

1、base case

先看递归的结束条件，有两种情况：

• cur= n的时候，直接填写1。
• cur>n时，或者index = coins.length时，直接填写0。

所以在dp表的最后一行中，只有当cur=n的时候，方法数才是1，也就是右下角位置（dp【最后一行】【最后一列】）的值是1。最后一行其他的位置的值，都是0。

dp[4][n] = 1; //对于这道题来说，最后一行就是4
//因为在java中，数组的默认值就是0，所以其余的位置就不必再填0了

2、普遍位置的推导

我们先来看填写好base case代码之后，整体代码是样子的。

 //经典的dp
    public static long moneyCombine2(int n) {
        if (n < 0) {
            return -1;
        }

        int[] coins = {1, 2, 5, 10};
        //根据递归的写法，可变参数也就是两个
        int[][] dp = new int[5][n + 1]; //行是硬币数，列是当前的钱数，返回左上角的值
        dp[4][n] = 1; //填写最后一行的数据，除了右下角是1，其他的全是0

        //普遍位置的填写如下
        for (int index = 3; index >= 0; index--) { //行数，从倒数第2行开始填
            for (int money = 0; money <= n; money++) { //列数，从第1列开始填
                
                //此处就是填写递归版本的代码，将递归函数改为dp表即可
                
            }
        }

        return dp[0][0] % 1000000007;
    }

在填写好base case之后，我们就需要进行其他中间位置的数值了。再次看递归版本的代码：

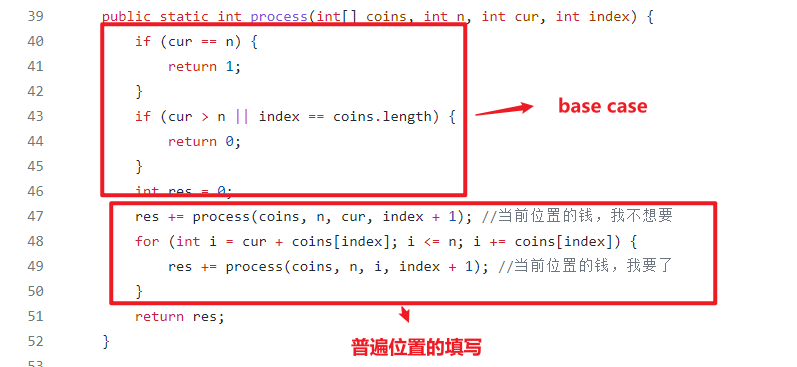
现在我们只需要将上图的普遍位置的填写，这段代码，写到上一段代码的两层for循环即可。然后将process改为dp表即可，如下：

 //经典的dp
    public static long moneyCombine2(int n) {
        if (n < 0) {
            return -1;
        }

        int[] coins = {1, 2, 5, 10};
        //根据递归的写法，可变参数也就是两个
        int[][] dp = new int[5][n + 1]; //行是硬币数，列是当前的钱数，返回左上角的值
        dp[4][n] = 1; //填写最后一行的数据，除了右下角是1，其他的全是0

        //普遍位置的填写如下
        for (int index = 3; index >= 0; index--) { //行数，从倒数第2行开始填
            for (int money = 0; money <= n; money++) { //列数，从第1列开始填
                
                //此处就是填写递归版本的代码，将递归函数改为dp表即可
                dp[index][money] = dp[index + 1][money]; //当前位置的硬币不要
                for (int cur = money + coins[index]; cur <= n; cur += coins[index]) { //递归过程的枚举过程
                    dp[index][money] += dp[index + 1][cur];
                    dp[index][money] %= 1000000007;
                }
                
            }
        }
        return dp[0][0] % 1000000007;
    }

切记切记，递归的代码是怎么写的，dp表里面就怎么填。我们只需要将递归函数的子过程，从dp表中取数据即可。取模运算是题意要求取模的。

总结：本质上，动态规划就是在将递归函数做的事，进行简化，递归函数可能去计算时，要递归多次，但是动态规划不一样，只需要在dp表中，直接拿取相应位置的数据即可。

三、斜率优化

其实上面写的dp，只是较为经典的写法，本质上，这段代码还是存在一定的小问题，那就是存在枚举问题，也就是说，效率还不够高。还可以进行优化。如下图：

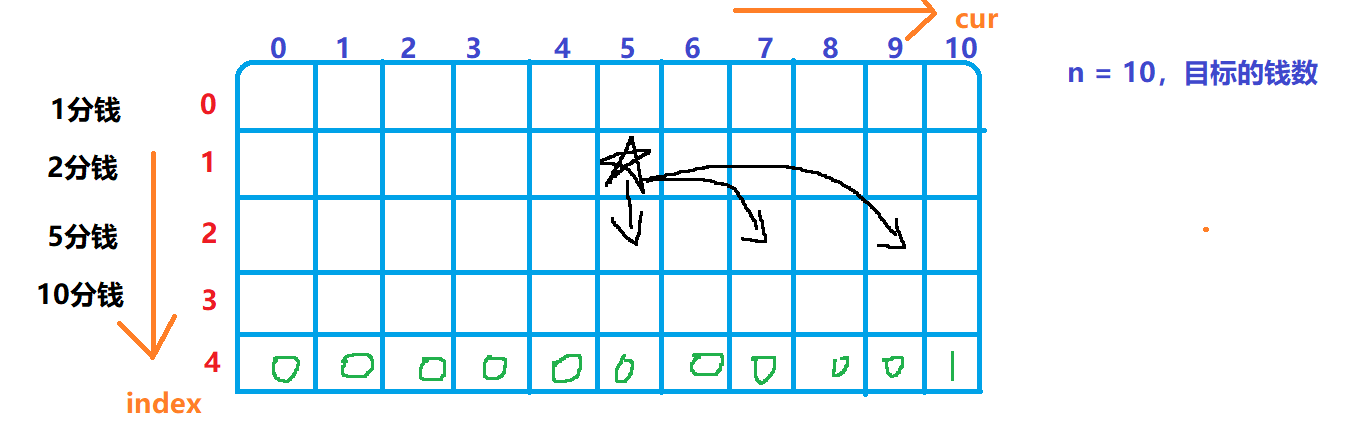
如上图所示，假设需要计算五角星位置的值，它所在的行是1，也就是2分钱的硬币，它所在的列是5，也就是当前有5分钱。根据递归函数可知，它依赖于dp【index+1】【cur】+ dp【index + 1】【cur + 2】+ dp【index+ 1】【cur + 4】……。

也就是说，它的数值，就等于它下一行的某些位置的数据进行求和。而具体下一行的哪些位置，取决于五角星的所在行，拿上图的举例，五角星的行数是1，对应的硬币面值是2，所以从五角星下面一行（dp【index】【cur】）位置开始，往右边进行求和，每次向右跳两个格子。这样的代码还不叫斜率优化，这只是一个依赖关系的推导，我们先来看看代码，其实和上文中的经典dp的解法一个意思，这里只是为了铺垫后续的斜率优化。

在上文的经典dp代码中，我们的列数，是从左往右计算的，此时我们需要稍微改一下。改成从右往左计算。如下：

 //优化的dp，从右往左遍历，没有枚举过程
public static int moneyCombine4(int n) {
    if (n < 0) {
        return -1;
    }

    int[] coins = {1, 2, 5, 10};
    //根据递归的写法，可变参数也就是两个
    int[][] dp = new int[5][n + 1]; //行是硬币数，列是当前的钱数，返回左上角的值
    dp[4][n] = 1; //填写最后一行的数据，除了右下角是1，其他的全是0

    //整体是从下往上，从右往左的
    for (int index = 3; index >= 0; index--) { //从倒数第二行开始填写
        for (int money = n; money >= 0; money--) { //从最后一列开始填写
            
            //此处就是填写递归版本的代码，将递归函数改为dp表即可
            dp[index][money] = dp[index + 1][money]; //当前位置的硬币不要
            for (int cur = money + coins[index]; cur <= n; cur += coins[index]) { //递归过程的枚举过程
                dp[index][money] += dp[index + 1][cur];
                dp[index][money] %= 1000000007;
            }
            
        }
    }
    return (int) dp[0][0];
}

上诉代码，就是将列（money），改为从右向左计算的。跟原来的没啥区别，重点就来了。好好看一下图：

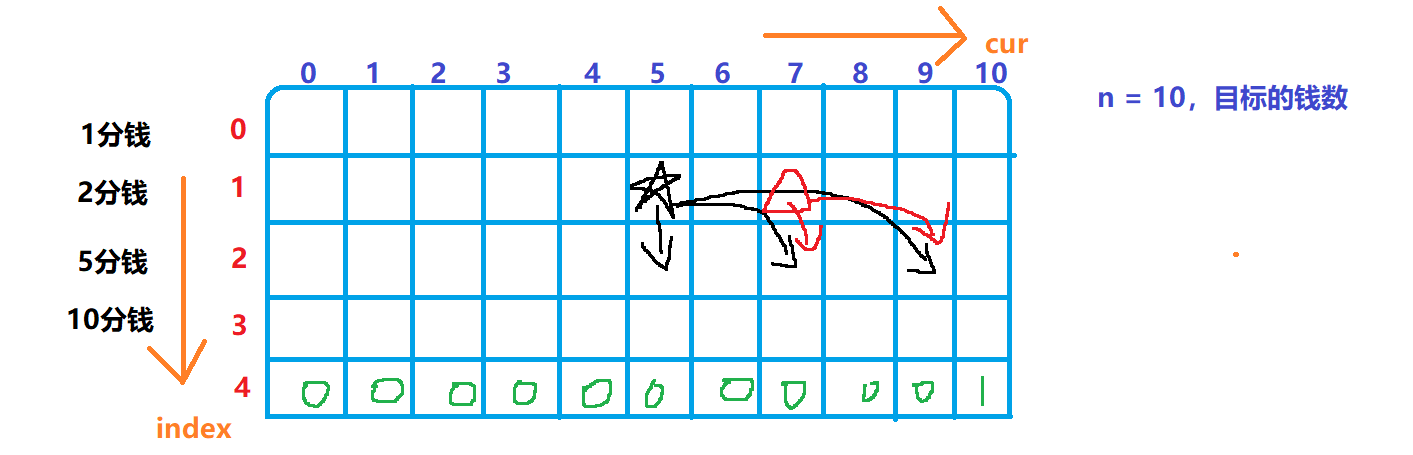
红色三角形位置的数值，求和，也是依赖于它下一行的某些位置的数据。很明显可以看出来，这些数据跟五角星的求和时，有很多都是来自同一个位置的数据，比如上图的dp【2】【7】+dp【2】【9】。也就是说，在计算五角星的时候，其实红色三角形位置的数据，已经帮我们计算过了，我们只需要从红色三角形位置拿取数据，然后再加上五角星下边的数据，就能得到五角星的数据啦。这样的优化，就称为斜率优化。

代码如下：

 //优化的dp，从右往左遍历，没有枚举过程
public static int moneyCombine4(int n) {
    if (n < 0) {
        return -1;
    }

    int[] coins = {1, 2, 5, 10};
    //根据递归的写法，可变参数也就是两个
    int[][] dp = new int[5][n + 1]; //行是硬币数，列是当前的钱数，返回左上角的值
    dp[4][n] = 1; //填写最后一行的数据，除了右下角是1，其他的全是0

    //整体是从下往上，从右往左的
    for (int index = 3; index >= 0; index--) { //从倒数第二行开始填写
        for (int money = n; money >= 0; money--) { //从最后一列开始填写
            
            //此处就是填写递归版本的代码，将递归函数改为dp表即可
            if (money + coins[index] <= n) { //在列数不越界的情况下，拿取数据
                dp[index][money] = dp[index][money + coins[index]] + dp[index + 1][money];
                dp[index][money] %= 1000000007;
            } else {
                dp[index][money] = dp[index + 1][money]; //直接拿取下边的值
            }
            
        }
    }
    return (int) dp[0][0];
}

以上的代码，就是斜率优化之后的代码，是不是很简单呢？

四、dp空间压缩

说到这里，我相信很多同学都已经知道这道题的整体思路了，空间压缩也就很简单了。整张dp表的填写，我们都是从最后一行开始填写，一直填写到第一行，然后第一行的第一个数据就是最终的答案。

并且我们还可以知道，计算普遍位置的时候，比如五角星的时候，我们只用到了五角星下面的一行数据。像这样的，依赖关系只来自于有限的行数据，那么就可以进行空间压缩。我们只需要建立一个一维数组，就解决这道题。

整体的思路，还是从最后一行开始填写，从下往上，从左往右填写：

 //dp空间压缩
    public static int moneyCombine5(int n) {
        if (n < 0) {
            return 0;
        }

        int[] coins = {1, 2, 5, 10};
        int[] dp = new int[n + 1]; //一维数组，从右向左开始填写
        dp[n] = 1; //右下角的值是1
        for (int index = 3; index >= 0; index--) {//行数
            for (int money = n; money >= 0; money--) {
                if (money + coins[index] <= n) {
                    dp[money] += dp[money + coins[index]];
                    dp[money] %= 1000000007;
                } //else情况，也就是直接拿取它下边的值，在这里就直接不动了
            }
        }
        return dp[0];
    }

好啦，以上全部就是本道题的全部讲解啦！！！如若文中有误，还望大家能够指正出来。又或者大家还有什么疑惑的地方，我们在评论区见吧！！！下期再见啦，拜拜！！！