目录
前言
●数据结构作为计算机专业基础课,综合性强,抽象性高,在一定程度上增加了学习难度,本次我们共同从数据结构的基础探讨,由浅入深进行数据结构的学习。
●由于作者水平有限,文章难免存在谬误之处,敬请读者斧正,俚语成篇,恳望指教!
●本文只浅显的探讨了链表的基本知识,作者相信随着学习课程的深入,我们将会对数据结构有更深的理解与收获!
正文
一,链表
引言:上篇文章介绍了有关线性表的顺序表部分,本篇文章将共同探讨线性表的链式存储结构——链表
1.什么是链表?
2.与链式存储有关的术语:
区别:① 无头结点 ② 有头结点
3.在链表中设置头结点有什么好处?
头结点的数据域内装的是什么?
4.链表(链式存储结构)的特点:
优点:数据元素的个数可以自由扩充 插入、删除等操作不必移动数据,只需修改链接指针,修改效率较高
缺点:存储密度小 存取效率不高,必须采用顺序存取,即存取数据元素时,只能按链表的顺序进行访问(顺藤摸瓜)
5.单链表的定义和实现:
(1)单链表的存储结构定义:
(2)单链表基本操作的实现:
初始化 ,取值,查找, 插入 ,删除
(3)单链表的运算时间效率分析:
单链表的尾插法:
6.循环链表
7.双向链表
8.顺序表和链表的比较
9. 线性表的合并
有序的链表合并
10.链表的应用
总结:
●由于作者水平有限,文章难免存在谬误之处,敬请读者斧正,俚语成篇,恳望指教!
前言
●数据结构作为计算机专业基础课,综合性强,抽象性高,在一定程度上增加了学习难度,本次我们共同从数据结构的基础探讨,由浅入深进行数据结构的学习。
●由于作者水平有限,文章难免存在谬误之处,敬请读者斧正,俚语成篇,恳望指教!
●本文只浅显的探讨了链表的基本知识,作者相信随着学习课程的深入,我们将会对数据结构有更深的理解与收获!
正文
一,链表
引言:上篇文章介绍了有关线性表的顺序表部分,本篇文章将共同探讨线性表的链式存储结构——链表
1.什么是链表?
将每个元素放在一个独立的存储单元中,元素间的逻辑关系依靠存储单元中附加的指针来给出。这种采用链式存储结构存储的线性表,称为链表。

2.与链式存储有关的术语:
①结点:数据元素的存储映像。由数据域和指针域两部分组成
②链表: n 个结点由指针链组成一个链表。它是线性表的链式存储映像,称为线性表的链式存储结构
③单链表、双链表、循环链表:
结点只有一个指针域的链表,称为单链表或线性链表
有两个指针域的链表,称为双链表
首尾相接的链表,称为循环链表
④头指针、头结点和首元结点
头指针是指向链表中第一个结点的指针
首元结点是指链表中存储第一个数据元素a1的结点
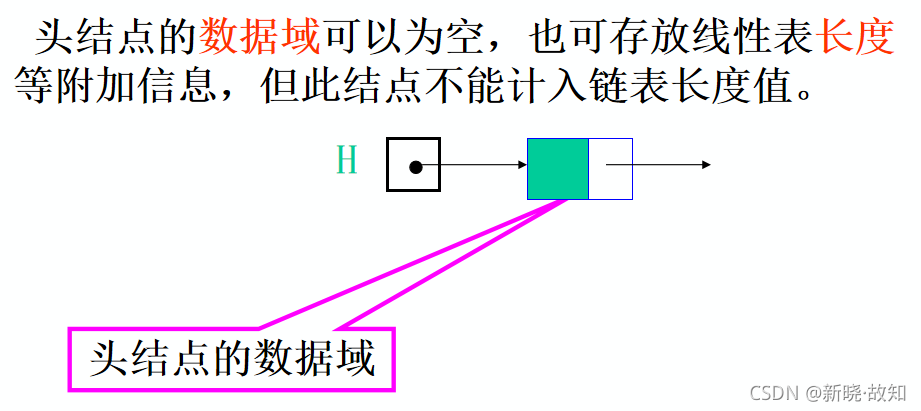
头结点是在链表的首元结点之前附设的一个结点;数据域内只放空表标志和表长等信息
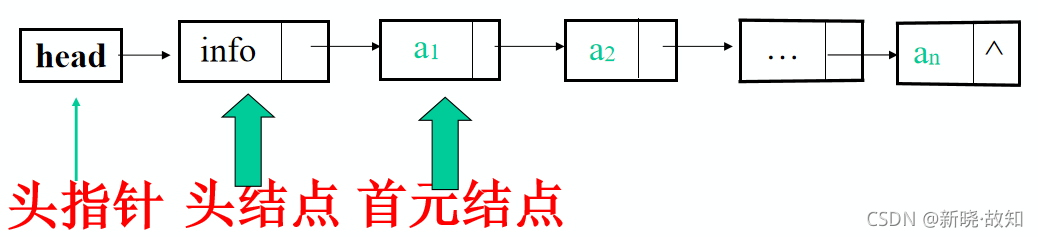
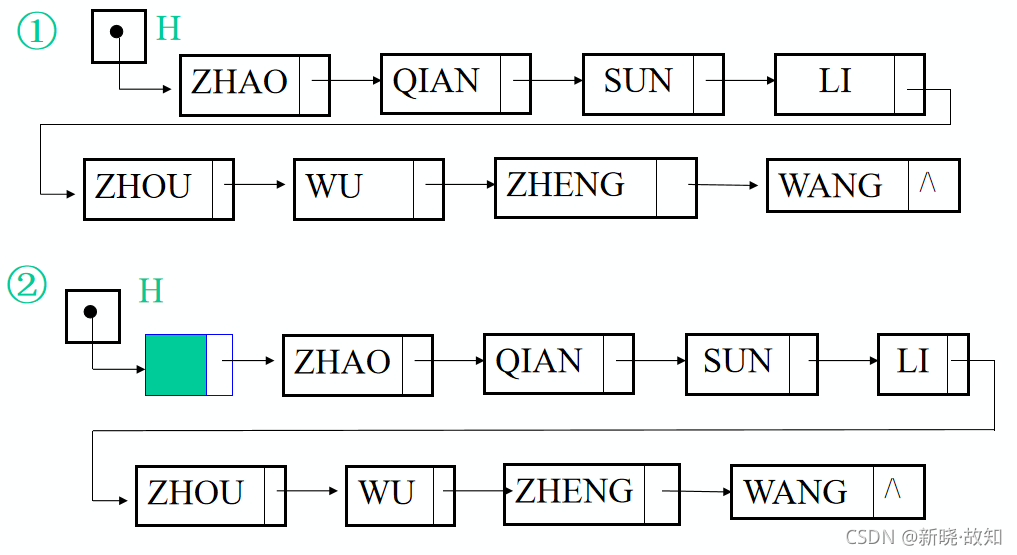
区别:① 无头结点 ② 有头结点
 3.在链表中设置头结点有什么好处?
3.在链表中设置头结点有什么好处?
① 便于首元结点的处理 首元结点的地址保存在头结点的指针域中,所以在链表的第一个位置上的操作和其它位置一致,无须进行特殊处理;
② 便于空表和非空表的统一处理 无论链表是否为空,头指针都是指向头结点的非空指针,因此空表和非空表的处理也就统一了。
头结点的数据域内装的是什么?
4.链表(链式存储结构)的特点:
(1)结点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻
(2)访问时只能通过头指针进入链表,并通过每个结点的指针域向后扫描其余结点,所以寻找第一个结点和最后一个结点所花费的时间不等
这种存取元素的方法被称为顺序存取法
优点:数据元素的个数可以自由扩充 插入、删除等操作不必移动数据,只需修改链接指针,修改效率较高
缺点:存储密度小 存取效率不高,必须采用顺序存取,即存取数据元素时,只能按链表的顺序进行访问(顺藤摸瓜)
5.单链表的定义和实现:

(1)单链表的存储结构定义:

单链表的存储结构定义
typedef struct LNode{
ElemType data; //数据域
struct LNode *next; //指针域
}LNode,*LinkList;
// *LinkList为Lnode类型的指针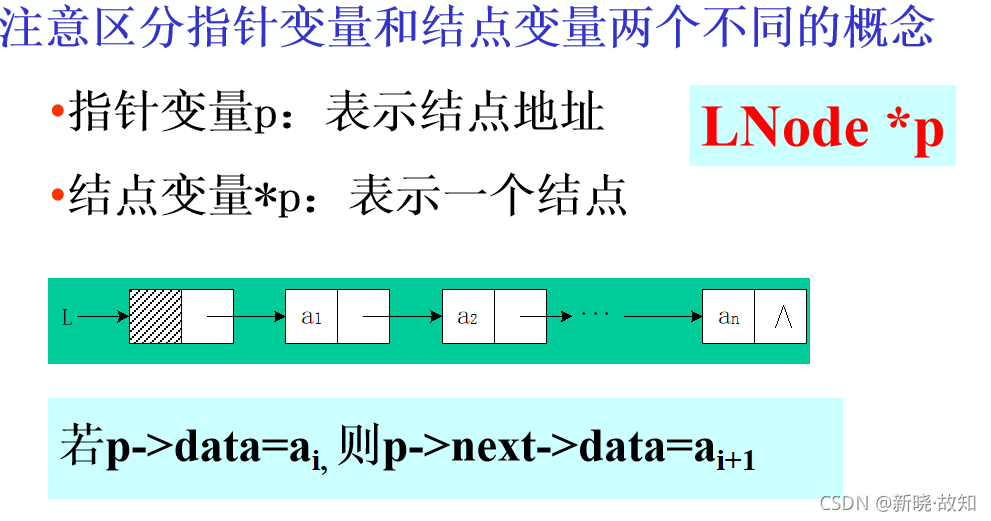
(2)单链表基本操作的实现:
初始化 ,取值,查找, 插入 ,删除
单链表初始化算法:
【单链表初始化算法】
Status InitList_L(LinkList &L){
L=new LNode;
L->next=NULL;
return OK;
}
单链表的销毁算法:
单链表的销毁算法
Status DestroyList_L(LinkList &L){
LinkList p;
while(L)
{
p=L;
L=L->next;
delete p;
}
return OK;
}
单链表的清空算法:
单链表的清空算法
Status ClearList(LinkList & L){
// 将L重置为空表
LinkList p,q;
p=L->next; //p指向第一个结点
while(p) //没到表尾
{ q=p->next; delete p; p=q; }
L->next=NULL; //头结点指针域为空
return OK;
}
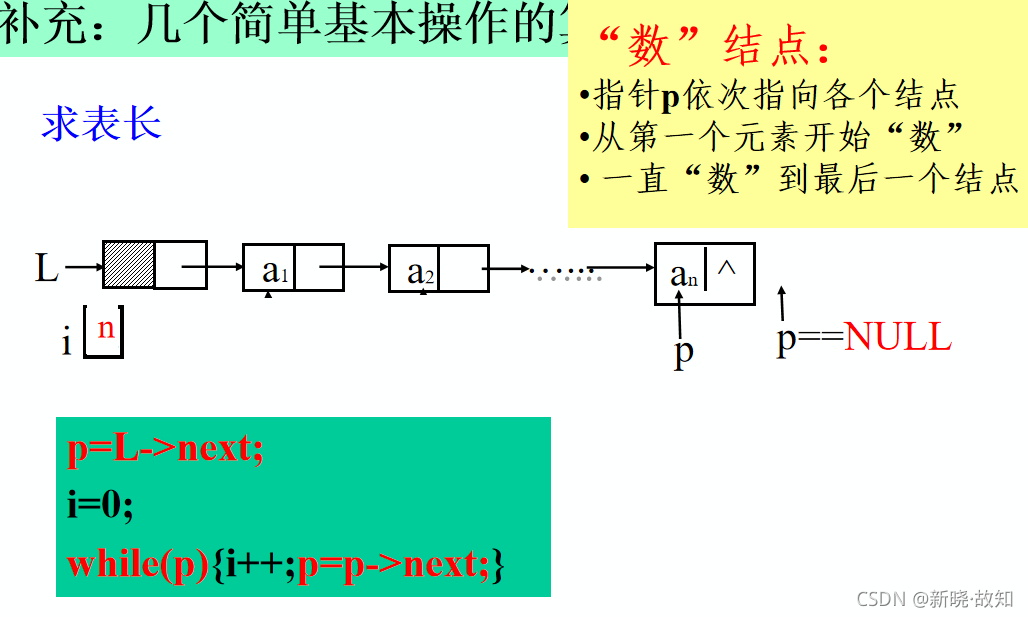
单链表的求表长算法:
单链表的求表长算法
int ListLength_L(LinkList L){
//返回L中数据元素个数
LinkList p;
p=L->next; //p指向第一个结点
i=0;
while(p){//遍历单链表,统计结点数
i++;
p=p->next; }
return i;
}
判断单链表是否为空:
判断单链表是否为空
int ListEmpty(LinkList L){
//若L为空表,则返回1,否则返回0
if(L->next) //非空
return 0;
else
return 1;
}
单链表的查找:
要从链表的头指针出发,顺着链域next逐个结点往下搜索,直至搜索到第i个结点为止。因此,链表不是随机存取结构
获取线性表L中的某个数据元素的内容
Status GetElem_L(LinkList L,int i,ElemType &e){
p=L->next;j=1; //初始化
while(p&&j<i){ //向后扫描,直到p指向第i个元素或p为空
p=p->next; ++j;
}
if(!p || j>i)return ERROR; //第i个元素不存在
e=p->data; //取第i个元素
return OK;
}//GetElem_L
在线性表L中查找值为e的数据元素
int LocateELem_L (LinkList L,Elemtype e) {
//返回L中值为e的数据元素的位置序号,查找失败返回0
p=L->next; j=1;
while(p &&p->data!=e)
{p=p->next; j++;}
if(p) return j;
else return 0;
}
插入(插在第 i 个结点之前)

(1)找到ai-1存储位置p
(2)生成一个新结点*s
(3)将新结点*s的数据域置为x
(4)新结点*s的指针域指向结点ai
(5)令结点*p的指针域指向新结点*s
在L中第i个元素之前插入数据元素e
Status ListInsert_L(LinkList &L,int i,ElemType e){
p=L;j=0;
while(p&&j<i−1){p=p->next;++j;} //寻找第i−1个结点
if(!p||j>i−1)return ERROR; //i大于表长 + 1或者小于1
s=new LNode; //生成新结点s
s->data=e; //将结点s的数据域置为e
s->next=p->next; //将结点s插入L中
p->next=s;
return OK;
}//ListInsert_L
删除(删除第 i 个结点)
将表的第i个结点删去 步骤:
(1)找到ai-1存储位置p
(2)保存要删除的结点的值
(3)令p->next指向ai的直接后继结点
(4)释放结点ai的空间
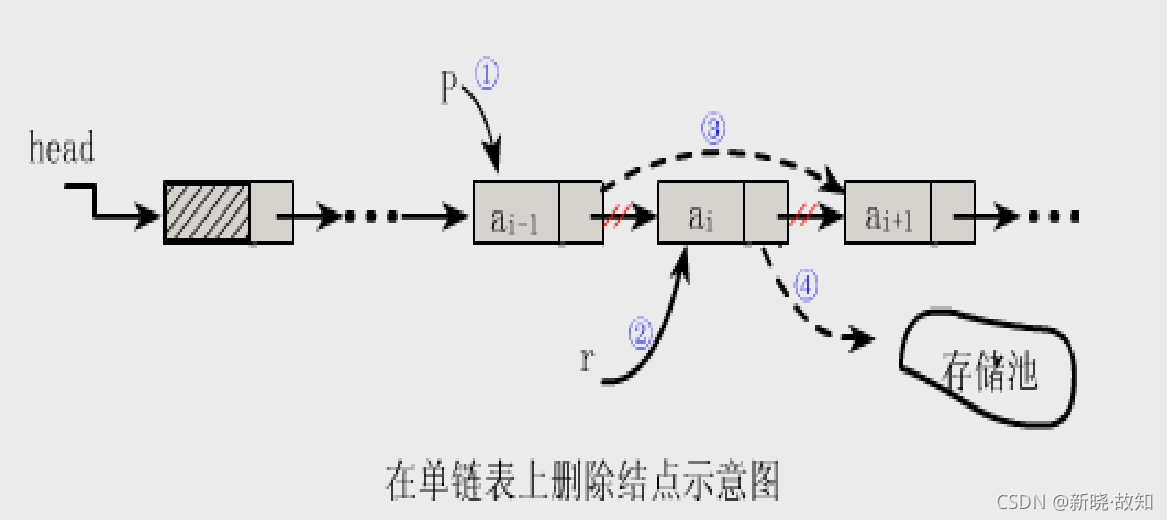
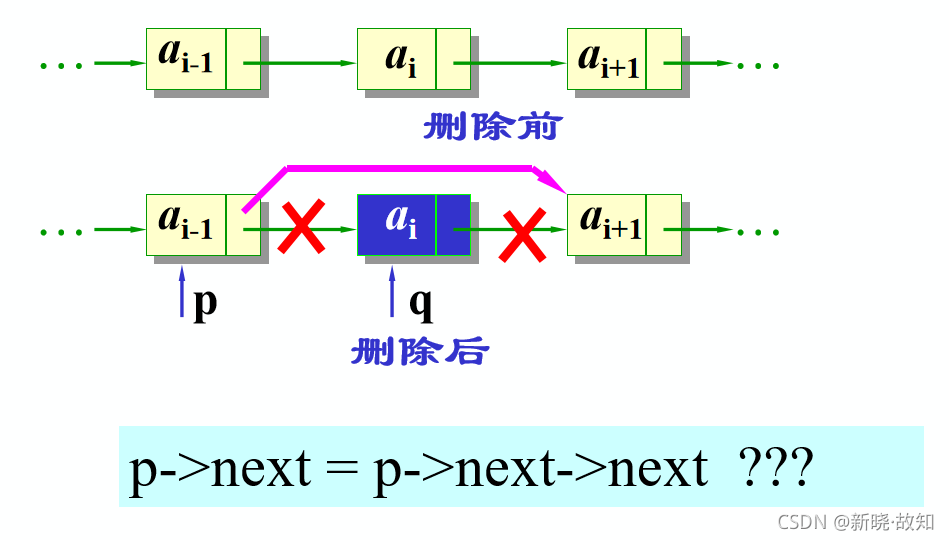
单链表的删除算法:
(1)找到ai-1存储位置p
(2)临时保存结点ai的地址在q中,以备释放
(3)令p->next指向ai的直接后继结点
(4)将ai的值保留在e中
(5)释放ai的空间
将线性表L中第i个数据元素删除
Status ListDelete_L(LinkList &L,int i,ElemType &e){
p=L;j=0;
while(p->next &&j<i-1){//寻找第i个结点,并令p指向其前驱
p=p->next; ++j;
}
if(!(p->next)||j>i-1) return ERROR; //删除位置不合理
q=p->next; //临时保存被删结点的地址以备释放
p->next=q->next; //改变删除结点前驱结点的指针域
e=q->data; //保存删除结点的数据域
delete q; //释放删除结点的空间
return OK;
}//ListDelete_L
(3)单链表的运算时间效率分析:


单链表的前插法(头插法)算法
void CreateList_F(LinkList &L,int n){
L=new LNode;
L->next=NULL; //先建立一个带头结点的单链表
for(i=n;i>0;--i){
p=new LNode; //生成新结点
cin>>p->data; //输入元素值
p->next=L->next;L->next=p; //插入到表头
}
}//CreateList_F
单链表的尾插法:
单链表的尾插法算法:
void CreateList_L(LinkList &L,int n){
//正位序输入n个元素的值,建立带表头结点的单链表L
L=new LNode;
L->next=NULL;
r=L; //尾指针r指向头结点
for(i=0;i<n;++i){
p=new LNode; //生成新结点
cin>>p->data; //输入元素值
p->next=NULL; r->next=p; //插入到表尾
r=p; //r指向新的尾结点
}
}//CreateList_L
6.循环链表

7.双向链表
双向链表的存储结构定义
typedef struct DuLNode{
ElemType data;
struct DuLNode *prior;
struct DuLNode *next;
}DuLNode, *DuLinkList
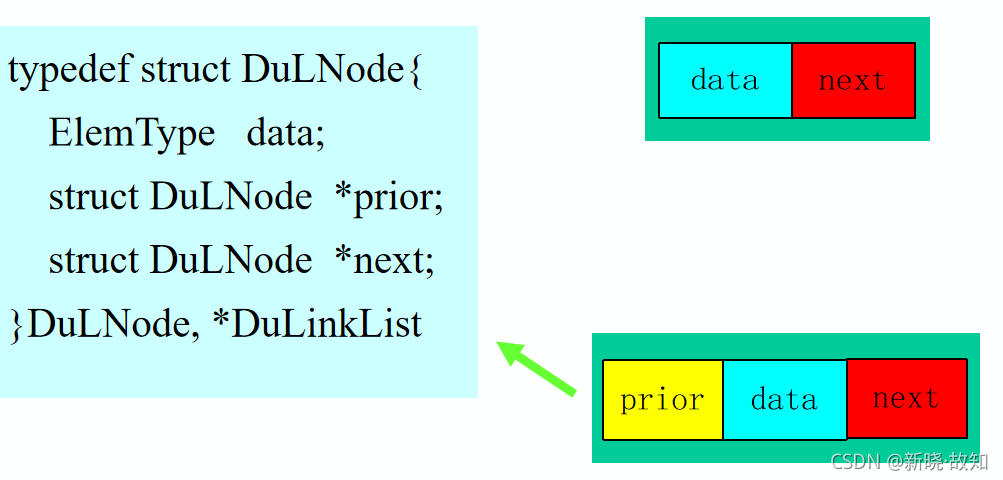

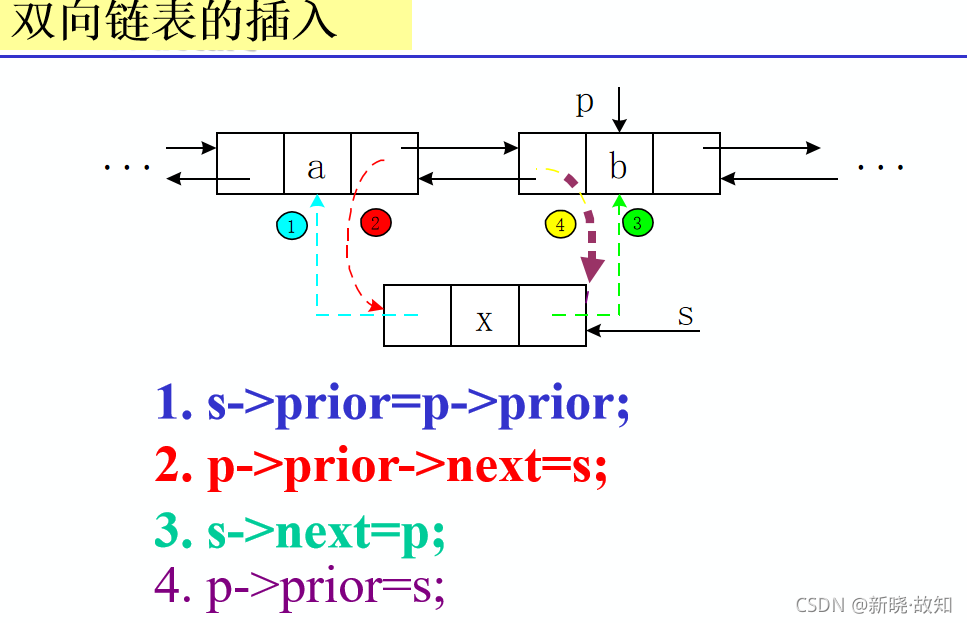
双向链表的插入算法
Status ListInsert_DuL(DuLinkList &L,int i,ElemType e){
if(!(p=GetElemP_DuL(L,i))) return ERROR;
s=new DuLNode;
s->data=e;
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
return OK;
}

双向链表的删除算法
Status ListDelete_DuL(DuLinkList &L,int i,ElemType &e){
if(!(p=GetElemP_DuL(L,i))) return ERROR;
e=p->data;
p->prior->next=p->next;
p->next->prior=p->prior;
delete p;
return OK;
}
8.顺序表和链表的比较
| 存储结构 比较项目 | 顺序表 | 链表 | |
| 空间 | 存储空间 | 预先分配,会导致空间闲置或溢出现象 | 动态分配,不会出现存储空间闲置或溢出现象 |
| 存储密度 | 不用为表示结点间的逻辑关系而增加额外的存储开销,存储密度等于1 | 需要借助指针来体现元素间的逻辑关系,存储密度小于1 | |
| 时间 | 存取元素 | 随机存取,按位置访问元素的时间复杂度为O(1) | 顺序存取,按位置访问元素时间复杂度为O(n) |
| 插入、删除 | 平均移动约表中一半元素,时间复杂度为O(n) | 不需移动元素,确定插入、删除位置后,时间复杂度为O(1) | |
| 适用情况 | ① 表长变化不大,且能事先确定变化的范围 ② 很少进行插入或删除操作,经常按元素位置序号访问数据元素 | ① 长度变化较大 ② 频繁进行插入或删除操作 | |
9. 线性表的合并
void union(List &La, List Lb){
La_len=ListLength(La);
Lb_len=ListLength(Lb);
for(i=1;i<=Lb_len;i++){
GetElem(Lb,i,e);
if(!LocateElem(La,e))
ListInsert(&La,++La_len,e);
}
}
有序的链表合并
void MergeList_L(LinkList &La,LinkList &Lb,LinkList &Lc){
pa=La->next; pb=Lb->next;
pc=Lc=La; //用La的头结点作为Lc的头结点
while(pa && pb){
if(pa->data<=pb->data){ pc->next=pa;pc=pa;pa=pa->next;}
else{pc->next=pb; pc=pb; pb=pb->next;}
pc->next=pa?pa:pb; //插入剩余段
delete Lb; //释放Lb的头结点}
10.链表的应用
应用(1)a.多项式创建---【算法步骤】
① 创建一个只有头结点的空链表。
② 根据多项式的项的个数n,循环n次执行以下操作: 生成一个新结点*s;
输入多项式当前项的系数和指数赋给新结点*s的数据域;
设置一前驱指针pre,用于指向待找到的第一个大于输入项指数的结点的前驱,pre初值指向头结点;
指针q初始化,指向首元结点;
循链向下逐个比较链表中当前结点与输入项指数,找到第一个大于输入项指数的结点*q;
将输入项结点*s插入到结点*q之前。
void CreatePolyn(Polynomial &P,int n)
{//输入m项的系数和指数,建立表示多项式的有序链表P
P=new PNode;
P->next=NULL; //先建立一个带头结点的单链表
for(i=1;i<=n;++i) //依次输入n个非零项
{
s=new PNode; //生成新结点
cin>>s->coef>>s->expn; //输入系数和指数
pre=P; //pre用于保存q的前驱,初值为头结点
q=P->next; //q初始化,指向首元结点
while(q&&q->expn<s->expn) //找到第一个大于输入项指数的项*q
{
pre=q;
q=q->next;
} //while
s->next=q; //将输入项s插入到q和其前驱结点pre之间
pre->next=s;
} //for
}
b.多项式相加---【算法步骤】
① 指针p1和p2初始化,分别指向Pa和Pb的首元结点。
② p3指向和多项式的当前结点,初值为Pa的头结点。
③ 当指针p1和p2均未到达相应表尾时,则循环比较p1和p2所指结点对应的指数值(p1->expn与p2->expn),有下列3种情况: 当p1->expn等于p2->expn时,则将两个结点中的系数相加,若和不为零,则修改p1所指结点的系数值,同时删除p2所指结点,若和为零,则删除p1和p2所指结点; 当p1->expn小于p2->expn时,则应摘取p1所指结点插入到“和多项式”链表中去; 当p1->expn大于p2->expn时,则应摘取p2所指结点插入到“和多项式”链表中去。
④ 将非空多项式的剩余段插入到p3所指结点之后。
⑤ 释放Pb的头结点。
应用(2)
约瑟夫环问题的具体描述是:设有编号为1,2,…,n的n(n>0)个人围成一个圈,从某个人开始报数,报到m时停止报数,报m的人出圈,再从他的下一个人起重新报数,报到m时停止报数,报m的出圈,……,如此下去,直到所有人全部出圈为止。当任意给定n和m后,设计算法求n个人出圈的次序。 显然,循环单链表可以很好地描述这个问题。我们将编号为1,2,…,n的n(n>0)个人围成一个圈表示成一个不带头结点的循环单链表L,其中L指向第一个结点,每个编号对应一个结点,

创建n个编号结点的循环单链表如算法:
void Create_L(LinkList &L,int n)
{
int i;
LNode *s,*r;
L=NULL;
r=L;
for(i=1;i<=n;i++)
{ s=(LinkList)malloc(sizeof(LNode));
s->data=i;
if(L==NULL){L=s; r=s;}
else{r->next=s;r=r->next;}
}
r->next=L;
}
约瑟夫算法:
void Josephus(LinkList L,int k,int n,int m)
{
LNode *s;
LNode *t;
s=GetLinkList(L,k-1);
printf("所有人出队序列如下:\n");
while (s->next!=s)
{ for (int i=1; i<m; i++) //先数m-1个数
{
t=s;
s=s->next;
} //把数到m的人从链表中删除
t->next=s->next;
printf("%d\t",s->data); //输出数到m的人的编号
free(s);
s=t->next;
}
printf("%d\n",s->data); //输出最后一个人的编号
free(s);
}
假设调用函数为main函数,且已知n=6,m=4,k=3,调用函数如下:
void main()
{
LinkList L;
Create_L(L,6);
Josephus(L,3,6,4);
}
最后出队序列编号为6, 4, 3, 5, 2, 1。总结:
本文共同探讨了链表的相关内容,在日常生活中有极其丰富的应用,作者认为要认真对待数据结构的学习,搭建基本知识框架,随着日积月累的学习逐渐填补总结,从脚踏实地做起,祝愿大家能够熟悉掌握这门课程,并将其能够熟悉的应用!
耐心看到这里的小伙伴一定很棒!加油!路在脚下,梦在前方!