树
- 1.基本概念
- 节点的度
- 树的度
- 叶子节点
- 双亲节点(父节点)
- 孩子节点
- 树
- 2.二叉树(对树的逻辑结构添加约束)
- 二叉链表物理存储结构
- 二叉树的不同形态
- 对树的逻辑结构添加哪些约束条件
- 形态一、满二叉树
- 形态二、完全二叉树
- 完全二叉树的高度
- 二叉树的缺点
- 3.二叉查找树(Binary Search Tree)(二叉搜索树,二叉排序树)
- 二叉查找树的优点
- 二叉查找树的复杂度
- 4.自平衡二叉树(AVL树、平衡二叉查找树,继承二叉查找树)
- 约束
- 重新平衡机制
- 平衡因子
- 平衡二叉树的优缺点:
- 优点
- 缺点
- 5.红黑树(也是平衡二叉树的一种)
- 特点
- 平衡的定义
- 使用
- 红黑树的优缺点
- 缺点:
- 6.BTree(又叫 平衡多路查找树)
- 定义
- 7.B+Tree
- 定义
- 8.HashMap
- 部分源码
- hash()函数
- putVal()函数
- resize()函数
- 参考
1.基本概念

节点的度
定义: 节点分支的个数
树的度
定义: 这棵树所有节点的最大分支数, 也就是最大的**节点度**
叶子节点
定义: 节点度为0的节点
双亲节点(父节点)
孩子节点
与双亲节点 刚好相反,
每个节点的孩子节点,这些孩子节点是没有次序之分的 (可以想象为三位的空间结构)。
树
约束比较轻的逻辑结构
1.孩子节点的数量没有限制。
2.孩子节点之间的顺序没有限制。
2.二叉树(对树的逻辑结构添加约束)

二叉链表物理存储结构

二叉树的不同形态

对树的逻辑结构添加哪些约束条件
1.孩子节点最多有两个, 树的度最大为2
2.节点添加上次序, 左节点, 右节点
形态一、满二叉树
定义: 处理叶子节点都有左右两个孩子。
形态二、完全二叉树
完全二叉树的高度
h = 2^ h-1个节点
二叉树的缺点
正常情况下(比如 满二叉树)
可以基于二分查找的思想,快速的查找到某个节点,时间复杂度是O(logN)
极端情况下(比如 仅有左子树 或 仅有右子树):
二叉树可以退化成一个 链表, 这种二叉树查找的时间复杂度就变成了O(N)
为了防止极端链表二叉树的产生,引入了平衡二叉树
3.二叉查找树(Binary Search Tree)(二叉搜索树,二叉排序树)
定义:它或者是一棵空树,或者是具有下列性质的二叉树
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值
它的左、右子树也分别为二叉排序树。
二叉查找树的优点
二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;
二叉查找树的复杂度
不论哪一种操作,所花的时间都和树的高度成正比。因此,如果共有n个元素,那么平均每次操作需要O(logn)的时间。
4.自平衡二叉树(AVL树、平衡二叉查找树,继承二叉查找树)
约束
可以是空树。
假如不是空树,任何一个结点的左子树与右子树都是平衡二叉树,并且高度之差的绝对值不超过 1。
任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。
重新平衡机制
增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡
平衡因子
定义: 某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子(BF,Balance Factor)
平衡二叉树中不存在平衡因子大于 1 的节点。在一棵平衡二叉树中,节点的平衡因子只能取 0 、1
平衡二叉树的优缺点:
优点
解决了 二叉树退化为近似链表结构,将时间复杂度控制为O(logN)
缺点
要求过于严格
要求每个节点的 左子树 与 右子树的最大高度差为1; 基于该要求 添加一个节点或删除一个节点时,会自动触发节点的左旋 或 右旋,以寻求整棵树的高度差最大为1
5.红黑树(也是平衡二叉树的一种)
特点
性质1. 结点是红色或黑色。
性质2. 根结点是黑色
性质3. 所有叶子都是黑色
性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
性质5. 从任一节结点其每个叶子的所有路径都包含相同数目的黑色结点。这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。
平衡的定义
红黑树上的任意节点,到任意的叶子节点的路径上经过的 黑节点 的个数必须是相同的。
或者说: 左右树的深度最大差 一倍(平衡树的条件比较宽松)。
优点: 写入效率相对(AVL树)要高一下。
使用
java中的TreeSet HashMap 均使用了红黑树的结构
红黑树的优缺点
缺点:
由于红黑树数是 严格的二叉树,所以当节点过多时(比如 1千万个),会导致整棵树的高度过高,导致查找性能降低。
为了解决查找的新能问题,引出了 BTree 平衡多路查找树
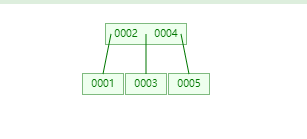
6.BTree(又叫 平衡多路查找树)

定义
B树又叫多叉树(相对于二叉树的叫法)
Mysql InnDB搜索引擎 使用的就是 B+Tree
排序方式:所有节点关键字是按递增次序排列,并遵循左小右大原则。
子节点数:非叶子节点的子节点数>1,且<=M ,且M>=2,空树除外(注:M 阶代表一个树节点最多有多少个查找路径,M=M路,当 M=2 则是二叉树)。
关键字数:枝节点的关键字数量大于等于 ceil(m/2)-1 个且小于等于 M-1 个(注:ceil()是个朝正无穷方向取整的函数。如ceil(1.1)结果为2)
所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为 null 对应下图最后一层节点的空格子。
7.B+Tree

定义
B+ 树跟 B 树不同。B+ 树的非叶子节点不保存关键字记录的指针,只进行数据索引,这样使得 B+ 树每个非叶子节点所能保存的关键字大大增加。
B+ 树叶子节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样。
B+ 树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。
非叶子节点的子节点数=关键字数
8.HashMap
部分源码
hash()函数
// 让key的hash值的高16位也参与路由寻址运算。(为什么使用高16位不太清楚,目的是减少hash碰撞)
// 路由寻址算法是 tab[i = (n - 1) & hash])
// ^ 二进制的异或算法,相同返回0,[0 0 =0; 1 1 = 0],不同返回1[0 1 =1; 1 0 =1]
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
putVal()函数
/**
* Implements Map.put and related methods
*
* @param hash hash for key
* @param key the key
* @param value the value to put
*
* @param onlyIfAbsent if true, don't change existing value(如果待写入的key已经存在时, true:不再写入操作,使用旧值; false:继续写入操作,覆盖旧值)
*
* @param evict if false, the table is in creation mode.(如果是fale,则创建新的table)
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; // 应用当前hashman的散列表
Node<K,V> p; // 当前散列表的元素
int n; // 散列表的长度
int i; // 路由寻址后的 tab的下标
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
// 寻址后的节点是非空的, 可能是链表,也可能是树
Node<K,V> e; // 临时元素
K k; // 临时元素的key
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// P的hash与 新节点的hash相等,且 key也想相等, 进行替换
e = p;
else if (p instanceof TreeNode)
// p节点已经树化
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// p节点为链表结构 Node
for (int binCount = 0; ; ++binCount) { // 迭代某一个链表
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash); // 树化操作
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize(); // 插入元素后,判断size是否大于阈值,进行扩容
afterNodeInsertion(evict);
return null;
}
resize()函数
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
参考
https://www.bilibili.com/video/BV1s54y1U7V3?p=2&spm_id_from=pageDriver