博弈论（Game Theory）入门学习笔记_dzc_go的博客

课程介绍

• 博弈论,又称对策论,是使用严谨的数学模型研究冲突对抗条件下最优决策问题的理论,是研究竞争的逻辑和规律的数学分支。

1-1 Taste-Backoff

• 以一个经典案例引出博弈论
• TCP Backoff Game
  两台电脑之间想要实现通信，两种方式可供选择，建立回退机制以及不建立回退机制。如果AB双方均建立回退机制，则双方延迟都是1。如果A、B一方建立回退机制，另一方不建立，那么建立的一方延迟是4，不建立的一方延迟是0。如果双方都不建立回退机制，则双方延迟都是3。
  
• 该问题的结果有一特点，即自己做出决策的收益不仅跟自己的决策有关，还跟对方的决策有关。因此存在一种“博弈”竞争关系。

1-2 Self-Interested Agents and Utility Theory

• Self-Interested Agents：利己代理
  并不是说决策者只考虑自己或者伤害他人，而是指决策者对于世界状态有自己的独特看法，并且根据自己的判断理解做出决策。
• Utility Theory ：效用理论
  每个决策者都有自己的效用函数，表达了决策者对于决策的偏好，决策者做出决策都是为了最大化效用期望。

1-3 Define

• Key Ingredients 关键组成
  Players：决策者。执行决策的人。
  Actions：动作。决策者可以做的事情。
  Payoffs：回报。激励决策者的东西，决策带来的回报。

• Two Standard Representations 两种标准表达方式
  Normal Form：分别定义Players、Actions、Payoffs。
  Extensive Form：扩展定义Timing、Information。

• 简单的博弈论问题可以使用矩阵表达，如1-1所示。

• 复杂问题无法用矩阵表达，如经典的造反问题。共有10000000个人，每个人可以选择造反或者不造反，只有达到2000000个人才算造反成功。如果造反达到人数要求，无论决策者选择什么收益都是1；如果造反没有达到人数要求，则决策者选择造反的收益是-1；如果造反没有达到人数要求，则决策者选择不造反的收益是0。
  Players： N = { 1 , . . . , 10 , 000 , 000 } N=\{1,...,10,000,000\} N={1,...,10,000,000}
  Actions Set for player i i i： A i = { R e v o l t , N o t } A_i=\{Revolt,Not\} Ai​={Revolt,Not}
  Utility Function for player i i i：
  （1） u i ( a i ) = 1   i f { j : a j = R e v o l t } > = 2 , 000 , 000 u_i(a_i)=1 \space if \{j:a_j=Revolt\}>=2,000,000 ui​(ai​)=1 if{j:aj​=Revolt}>=2,000,000
  （2） u i ( a i ) = − 1   i f { j : a j = R e v o l t } < 2 , 000 , 000   a n d   a i = R e v o l t u_i(a_i)=-1 \space if \{j:a_j=Revolt\}<2,000,000 \space and \space a_i=Revolt ui​(ai​)=−1 if{j:aj​=Revolt}<2,000,000 and ai​=Revolt
  （3） u i ( a i ) = − 0   i f { j : a j = R e v o l t } < 2 , 000 , 000   a n d   a i = N o t u_i(a_i)=-0 \space if \{j:a_j=Revolt\}<2,000,000 \space and \space a_i=Not ui​(ai​)=−0 if{j:aj​=Revolt}<2,000,000 and ai​=Not

1-4 Examples

• 囚徒困境 Prisoner’s dilemma。故事背景：两个共谋犯罪的人被关入监狱，不能互相沟通情况。如果两个人都不揭发对方，则由于证据不确定，每个人都坐牢一年；若一人揭发，而另一人沉默，则揭发者因为立功而立即获释，沉默者因不合作而入狱十年；若互相揭发，则因证据确凿，二者都判刑八年。由于囚徒无法信任对方，因此倾向于互相揭发，而不是同守沉默。
  结果的优劣程度按照A>B>C>D排序。
  

• Game of Pure Competition 纯竞争博弈
  博弈的双方具有完全对立的利益。
  对于双方任意动作组合，其效用之和永远为一个常数。 ∀   a ∈ A , u 1 ( a ) + u 2 ( a ) = c \forall \space a \in A,u_1(a)+u_2(a)=c ∀ a∈A,u1​(a)+u2​(a)=c
  特殊类型：零和博弈。双方效用之和永远为0。
  举例说明：石头剪刀布游戏。
  

• Games of Cooperation 合作博弈
  博弈的多方具有相同的利益，利益之间不存在冲突。 ∀ a ∈ A , ∀ i , j , u i ( a ) = u j ( a ) \forall a\in A,\forall i,j,u_i(a)=u_j(a) ∀a∈A,∀i,j,ui​(a)=uj​(a)
  举例说明：过马路问题。马路两头两个人想同时通行，每个人可以选择靠左或者靠右行驶。
  

1-5 Nash Equilibrium Intro

• Keynes Beauty Contest Game：凯恩斯选美博弈
  举办选美大赛，从1-100号候选者中选择自己认为最美的一位，获得票数最多的人获得选美冠军，投票给选美冠军的人也会得到一定的奖励。这个问题是老千层饼了，第一层的人只是自己觉得谁漂亮就选谁，比如A觉得10号最美投票给了10号；第二层的人考虑其他人的投票分布从而产生自己的决策，比如B觉得可能有很多人投票给30号，虽然自己喜欢10号也投票给30号；第三层的人觉得其他人可能也会因为考虑到第二层的因素，从而放弃自己最喜欢的转投自己认为最火爆的…这是一个无休止的猜想游戏。
• 猜数字游戏
  每个人从1-100中选择一个整数，最后最接近平均值三分之二的人获得奖励，假设参加这项游戏的人数足够多。这个问题同样是一个千层饼问题。
  第一层的人：参赛人数足够多，我假设大家所选择的数字均匀分布，那么最后的平均值应该接近于50。那么我为了获胜应该选择的数字是 50 ∗ 2 3 = 33 50*\frac{2}{3}=33 50∗32​=33。
  第二层的人：我想大部分人都在第一层，因此他们都选择33。那么最后的平均值应该接近于33。那么我为了获胜应该选择的数字是 33 ∗ 2 3 = 22 33*\frac{2}{3}=22 33∗32​=22。
  第三层的人： 22 ∗ 2 3 = 11 22*\frac{2}{3}=11 22∗32​=11。
  …
  第n层的人：应该选择的数是0。这就得到了纳什均衡。
  美国进行过一项调查，其中2%选择了66（没读懂题的笨蛋）、5%的选择了50（第一层）、10%的选择了33（第二层）、6%选择了22（第三层）、12%的选择了0或者1（思考到了最后）。但最后的结果平均值为19，第三层左右的人获得了最终的胜利。
• 以上两个故事告诉我们，在投资问题或者博弈问题中，我们的层数不可太高也不可太低。太低是傻子，太高聪明反被聪明误。

1-6 Strategic Reasoning

• 在其他人的决策确定的情况下，每一个决策者都是为了最大化个人的收获效用来做出决策。
• 一旦纳什均衡建立，没有人可以通过改变决策跳出均衡而获利受益。
• 如果某些决策者通过改变决策跳出均衡可以获利受益，那么说明纳什均衡还没有真正建立。
• 纳什均衡是一个稳定的状态，但并不是一个最优的获利状态。

1-7 Best Response and Nash Equilibrium

• Best Response 最优响应
  如果知道其他所有人的动作，那么挑选对于自己最有利的动作就变得十分简单。
  a i 表 示 第 i 个 决 策 者 所 做 出 的 决 策 a_i表示第i个决策者所做出的决策 ai​表示第i个决策者所做出的决策
  a − i = { a 1 , . . . , a i − 1 , a i + 1 , . . . , a n } 表 示 除 去 a i 以 外 其 他 人 的 决 策 a_{-i}=\{a_1,...,a_{i-1},a_{i+1},...,a_n\}表示除去a_i以外其他人的决策 a−i​={a1​,...,ai−1​,ai+1​,...,an​}表示除去ai​以外其他人的决策
  a = ( a i , a − i ) a=(a_i,a_{-i}) a=(ai​,a−i​)
  a i ∗ ∈ B R ( a − i )   i f f ∀ a i ∈ A i , u i ( a i ∗ , a − i ) > = u i ( a i , a − i ) a_i^*\in BR(a_{-i})\space iff \forall a_i\in A_i,u_i(a_i^*,a_{-i})>=u_i(a_i,a_{-i}) ai∗​∈BR(a−i​) iff∀ai​∈Ai​,ui​(ai∗​,a−i​)>=ui​(ai​,a−i​)
  其中 B R ( a − i ) BR(a_{-i}) BR(a−i​)表示已知其他决策信息后第i个决策者做出的最优响应，最优响应不一定只有一个。并且最优相应集合中的所有元素 a i ∗ a_i^* ai∗​都满足下列要求，当且仅当选择 a i ∗ a_i^* ai∗​的效用大于等于选择其他所有响应的效用。
• Pure Strategy Nash Equilibrium 纯策略纳什均衡
  实际上我们并不知道其他人会做出何种决策，因此根据他人决策制定自己的最优响应是不现实的。
  a = { a 1 , . . . , a n } i s   a   p u r e   s t r a t e g y   N a s h   e q u i l i b r i u m   i f f   ∀ i , a i ∈ B R ( a − i ) a=\{a_1,...,a_n\}is \space a \space pure \space strategy \space Nash \space equilibrium \space iff \space \forall i,a_i\in BR(a_{-i}) a={a1​,...,an​}is a pure strategy Nash equilibrium iff ∀i,ai​∈BR(a−i​)

1-8 Nash Equilibrium of Example Games

• 纳什均衡的定义
  给定其他决策者的决策，每个决策者都没有单独改变决策的动机。（也就是当前决策是最优决策）
  假设一共有A、B、C三个决策者，已知A、B决策下C做出最优决策 c ∗ c^* c∗，已知A、C决策下B做出最优决策 b ∗ b^* b∗，已知B、C决策下A做出最优决策 a ∗ a^* a∗，那么 ( a ∗ , b ∗ , c ∗ ) (a^*,b^*,c^*) (a∗,b∗,c∗)就是一个纳什均衡点。
• 如何从决策矩阵中挑选纳什均衡点？
  看该单元格，是否左侧的值是该列左侧值的最大值，右侧的值是否是该行右侧值的最大值。
• 纳什均衡不一定是对于全局来说最优的结果。比如囚徒困境。
• 纳什均衡也不是自发实现的，需要有一定的沟通协商规定，总之就是直接间接获取他人的决策信息。
  

1-9 Dominant Strategies

• Strictly\Very Weakly Dominates 决策优势、劣势关系
  s i   s t r i c t l y   d o m i n t a t e s   s i ′   i f ∀ s − i ∈ S − i , u i ( s i , s − i ) > u i ( s i ′ , s − i ) s_i \space strictly \space domintates \space s_i^{'} \space if \forall s_{-i}\in S_{-i},u_i(s_i,s_{-i})>u_i(s_i^{'},s_{-i}) si​ strictly domintates si′​ if∀s−i​∈S−i​,ui​(si​,s−i​)>ui​(si′​,s−i​)
  s i   v e r y   w e a k l y   d o m i n t a t e s   s i ′   i f ∀ s − i ∈ S − i , u i ( s i , s − i ) > = u i ( s i ′ , s − i ) s_i \space very \space weakly \space domintates \space s_i^{'} \space if \forall s_{-i}\in S_{-i},u_i(s_i,s_{-i})>=u_i(s_i^{'},s_{-i}) si​ very weakly domintates si′​ if∀s−i​∈S−i​,ui​(si​,s−i​)>=ui​(si′​,s−i​)
  严格压制关系与轻微压制关系的区别就在于取不取等号。以 s i s_i si​严格压制决策 s i ′ s_i^{'} si′​为例，是指无论其他决策者制定什么决策，当前决策者选择 s i s_i si​的效用一定严格优于选择 s i ′ s_i^{'} si′​。
• 如果一个决策压制其他所有决策，那么称之为占优策略。如果该决策严格压制每一个其他决策，那么称之为严格占优策略，并且该策略唯一。由占优策略组成的策略组合一定是纳什均衡点，全部由严格占优策略组成的策略组合一定是唯一的纳什均衡点。

1-10 Pareto Optimality

• 之前对于决策的选择以及评估都是站在每个决策者的角度，现在我们跳出决策者的身份，以一个外界观察者的角度来评估决策。我们只考虑最直接的一种评估方式，如果决策组合 O O O对于所有决策者的效用都优于决策 O ′ O^{'} O′，那么我们称 O   P a r e t o − d o m i n a t e s   O ′ O \space Pareto-dominates \space O^{'} O Pareto−dominates O′。
  比如说 O ( 7 , 8 ) 、 O ′ ( 4 , 5 ) ， 那 么 我 们 可 得 O   P a r e t o − d o m i n a t e s   O ′ O(7,8)、O^{'}(4,5)，那么我们可得O \space Pareto-dominates \space O^{'} O(7,8)、O′(4,5)，那么我们可得O Pareto−dominates O′。
• Pareto-Optimal 帕累托最优
  一个决策组合 O ∗ O^* O∗，如果没有其他任何一个决策组合帕累托压制 O ∗ O^* O∗,那么称该决策组合是帕累托最优。
  帕累托最优定义的并不是压制别人的能力，而是不被其他人压制。
  一场游戏中可能有多个帕累托最优决策组合。
  一场游戏中最少含有一个帕累托最优决策组合。
• 实例分析
  
  注意对于零和博弈问题来说，所有决策组合都是帕累托最优。

2-1 Mixed Strategies and Nash Equilibrium Taste

• 以安保设置检查关卡、攻击者制定策略攻击关卡的博弈问题来引出混合策略。

2-2 Mixed Strategies and Nash Equilibrium

• 纯策略每次决策选择的是具体的动作，而混合策略每次决策选择的是概率分布。纯策略纳什均衡是混合策略纳什均衡的一种。
• 纯策略均衡：每个决策者都是根据已知其他决策者的选择从而做出决策，并且在已知其他决策者选择的前提下没有改变自己决策的动机。混合策略均衡：每个决策者只可以调整自己的决策分布，而自己的效用则由其他决策者的决策分布决定。
• 在博弈游戏中，决策者每次选择固定的决策方式是最愚蠢的结果，因为竞争者会根据你的固定选择从而制定策略获利。因此决策者应该随机决策来迷惑对手，让对手猜不透你的选择。
• 区分定义：在纯策略中每个决策者每一步决定的是一个动作 a i a_i ai​；在混合策略中每个决策者每一步决定的是一个策略 s i s_i si​，策略包含多个动作及对应概率。针对第 i i i个决策者所有策略的组合为 S i = { s 1 , . . . , s n } S_i=\{s_1,...,s_n\} Si​={s1​,...,sn​}，针对所有决策者的策略组合为各个决策者的策略笛卡尔积 S = S 1 × . . . × S n S=S_1\times ...\times S_n S=S1​×...×Sn​。
• 在纯策略中我们针对每个决策者的不同动作衡量效用，在混合策略中我们针对每个决策者的不同策略概率分布来衡量效用，换句话说计算效用期望。
  u i ( s ) = ∑ a ∈ A u i ( a ) P r ( a ∣ s ) , P r ( a ∣ s ) = ∏ j ∈ N s j ( a j ) u_i(s)=\sum_{a\in A}u_i(a)Pr(a|s),Pr(a|s)=\prod_{j\in N}s_j(a_j) ui​(s)=∑a∈A​ui​(a)Pr(a∣s),Pr(a∣s)=∏j∈N​sj​(aj​)
• 混合策略中的最优响应以及纳什均衡
  只需要将之前的 a i a_i ai​全部替换成 s i s_i si​即可。
  s i ∗ ∈ B R ( s − i )   i f f ∀ s i ∈ S i , u i ( s i ∗ , s − i ) > = u i ( s i , s − i ) s_i^*\in BR(s_{-i})\space iff \forall s_i\in S_i,u_i(s_i^*,s_{-i})>=u_i(s_i,s_{-i}) si∗​∈BR(s−i​) iff∀si​∈Si​,ui​(si∗​,s−i​)>=ui​(si​,s−i​)
  s = { s 1 , . . . , s n } i s   a   N a s h   e q u i l i b r i u m   i f f   ∀ i , s i ∈ B R ( s − i ) s=\{s_1,...,s_n\}is \space a \space Nash \space equilibrium \space iff \space \forall i,s_i\in BR(s_{-i}) s={s1​,...,sn​}is a Nash equilibrium iff ∀i,si​∈BR(s−i​)
• 纳什理论
  每个有限游戏都有一个纳什均衡。（有限游戏是指有限的players、actions、utilities）。

2-3 Computing Mixed Nash Equilibrium

• 以行人问题作为示例，展示两种纳什均衡的求解方法。
  
  

2-4 Hardness Beyond 2x2 Games

• 本章节介绍算法求解纳什均衡问题的困难行与复杂度。
• 寻找NE（纳什均衡）的两个经典算法：
  LCP（Linear Complementarity）formulation 线性互补问题。
  Support Enumeration Method 子集枚举算法。
• NE求解是一个困难的问题，现在还没有一般的NE求解方法（不仅限于双矩阵博弈）。目前还没有求解NE的多项式时间算法，并且与NE有关的几个问题已经被证明是np-hard的（比如判断当前问题是否有多于一个NE）。
• 在4 人及以上的博弈中，纳什均衡的计算是属于PPAD-Complete 的。总结来说，PPAD介于NP与P之间。最外层的NPC问题是指在多项式时间内可以判断是否存在解，NP问题是指已知存在解但无法在多项式时间内求解，P问题是指可以在多项式时间内求解。

2-5 Example: Mixed Strategy Nash

• 本节我们以足球中点球大战的例子来体会混合策略纳什均衡在实际当中的应用。

• 点球大战说的是这么一种博弈游戏。点球者可选择向左向右踢，守门员可选择向左向右扑救。最简单的情况，我们默认守门员扑空的情况，点球者收益是1，守门员收益是0；守门员选对方向的情况，点球者收益是0，守门员收益是1。但是实际情况中，收到点球者球技的影响，守门员扑空时也不一定进球，比如说该球员右脚技术很差，即便扑空，也只有75%的概率进球。

• 最基础的点球大战收益矩阵：
  

• 调整后的点球大战收益矩阵：
  

• 守门员的决策分布使得点球者对自己的决策漠不关心（收益相等）：
  设守门员向左扑的概率为 q q q，向右扑的概率为 1 − q 1-q 1−q
  达到纳什均衡时，点球者向左向右踢得收益相同：
  q × 0 + ( 1 − q ) × 1 = q × 0.75 + ( 1 − q ) × 0 , q = 4 7 q\times 0+(1-q)\times 1=q\times 0.75+(1-q)\times 0,q=\frac{4}{7} q×0+(1−q)×1=q×0.75+(1−q)×0,q=74​

• 点球者的决策分布使得守门员对自己的决策漠不关心（收益相等）：
  设点球者向左踢的概率为 p p p，向右踢的概率为 1 − p 1-p 1−p
  达到纳什均衡时，守门员向左向右扑得收益相同：
  p × 1 + ( 1 − p ) × 0.25 = p × 0 + ( 1 − p ) × 1 , p = 4 7 p\times 1+(1-p)\times 0.25=p\times 0+(1-p)\times 1,p=\frac{4}{7} p×1+(1−p)×0.25=p×0+(1−p)×1,p=74​

• 分析以上结果，点球者知道自己的左脚更具有优势，因此增大向左踢的概率，最终达到纳什均衡有 4 7 \frac{4}{7} 74​的概率向左踢。守门员知道点球者左脚有优势会更多向左踢，因此增大向左扑的概率，最终达到纳什均衡有 4 7 \frac{4}{7} 74​的概率向左扑。

2-7 Data：Professional Sports and Mixed Strategies

• 上一节中我们利用收益矩阵理论分析了点球大战中的博弈情况，这一节我们通过真实实验数据去验证理论的正确性。

• 147场点球统计出的收益矩阵信息：
  

• 设点球者向左踢的概率为 P K P_K PK​，守门员向左扑的概率为 P G P_G PG​，计算纳什均衡点。
  
  

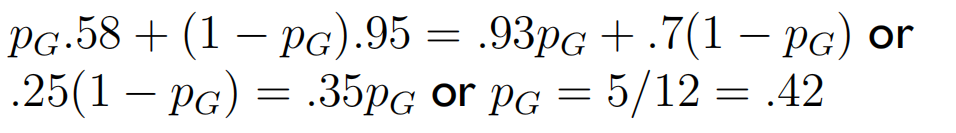
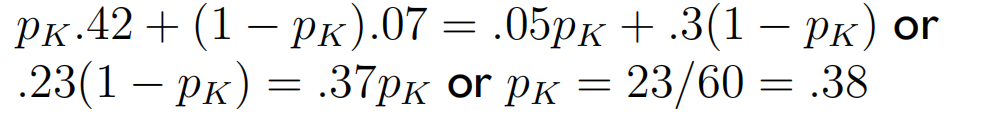
• 将计算出的概率与实际统计的概率相比，两者结果非常接近。证明纳什均衡理论的确是实际存在的、正确的理论，可以表征事物发展的内在规律。
  

3-1 Beyond the Nash Equilibrium

• 本章节用三张图片，三个故事分别引出Dominated Strategies、Zero-Sum Games、Coordination。

3-2 Strictly Dominated Strategies & Iterative Removal

• 本章节带来的是严格占优策略以及迭代消除法。
• Strictly Dominated Strategies 严格占优策略
  A strategy a i ∈ A i a_i\in A_i ai​∈Ai​is strictly dominated by a i ′ ∈ A i a_i^{'}\in A_i ai′​∈Ai​if u i ( a i , a − i ) < u i ( a i ′ , a − i ) ∀ a − i ∈ A − i u_i(a_i,a_{-i})<u_i(a_i^{'},a_{-i})\forall a_{-i}\in A_{-i} ui​(ai​,a−i​)<ui​(ai′​,a−i​)∀a−i​∈A−i​.
  简单来说，无论其他决策者作何决策，第 i i i个决策者选择 a i a_i ai​的收益都要大于选择 a i ′ a_i^{'} ai′​。
• 迭代消除法过程图示
  每次迭代消去针对的都是某一特定决策者，因此只需看对应的左侧收益或者是右侧收益，不用考虑虽然在左侧收益完全占优，但是右侧收益被消除的有更优的情况，因为博弈的过程是最大化个人收益，不会去考虑到其他决策者的收益。
  
  注意：迭代消除的过程同样也可以使用混合策略，比如说第二张图中，如果U行与D行以相同概率混合，混合结果同样严格占优M行，同样可以消除掉M行，虽然这里M行可以使用纯策略消除。因此给与我们提示，如果纯策略消除不掉的话或许可以尝试混合策略消除。
• 借助迭代消除的思想也可以找到纯策略纳什均衡点。
  具体方法是：找到每一行左侧收益的最大值标出，找到每一列右侧收益的最大值标出。如果某一个单元下标重合，那么就是纯策略纳什均衡点。
  
• 依据严格占优策略的迭代消除法会保持纳什均衡的性质（即不影响纳什均衡），并且迭代消除的顺序无关紧要（最终结果相同）。
• 弱占优策略
  相较于严格占优策略，弱占优策略的条件相对宽松了一些。严格占优策略要求针对所有的其他决策者决策，第 i i i个决策者选择 a i a_i ai​的收益都要优于 a i ′ a_i^{'} ai′​的收益。弱占优决策是指，针对所有的其他决策者决策，第 i i i个决策者选择 a i a_i ai​的收益都要大于等于 a i ′ a_i^{'} ai′​的收益，并且对于部分其他决策者的决策情况，第 i i i个决策者选择 a i a_i ai​的收益都要优于 a i ′ a_i^{'} ai′​的收益。总结来说弱占优策略部分满足严格占优策略的要求。
  弱占优策略同样可以用于迭代消除，但是迭代消除的顺序对结果有影响，至少一个纳什均衡点被保留。

3-3 Dominated Strategies & Iterative Removal:An Application

• 本章节介绍了一个十分有趣的实验来佐证，猪都不会去选择被严格压制的策略，更何况是人类。
• 实验内容是这样的，在一个大笼子里关着一头大猪和一头小猪，两头猪都在笼子的A侧，笼子的B侧有一个机关，触发该机关在笼子的A侧就会掉落下10份食物，无论大猪小猪从A侧跑到B侧触发机关再回到A侧都需要消耗2份食物。大猪会欺负小猪，不同情况下大猪小猪获得事物配比如下：
  如果大猪先得到食物，最终小猪获得1份，大猪获得9份。
  如果小猪先得到食物，最终小猪获得4份，大猪获得6份。
  如果大猪小猪同时获得，最终小猪获得3份，大猪获得7份。
• 该问题的收益矩阵如下图所示：
  
• 虽然无论谁先得到食物，都是大猪获益更多，但是对于小猪来说，正确的决策能增加自己的收益。选择花费2份食物代价去触发机关，也就以为着会较晚获得食物，因此看起来大猪小猪都选择等待是最好的选择，但同时也存在问题如果都不触发机关就都无法获得食物。
• 该问题中存在着严格占优策略，对于小猪来说，选择等待的收益永远大于选择触发的收益，因此小猪很大概率会选择等待。而大猪虽然也想“坐享其成”，但小猪的决策让大猪不得不更多时候选择去触发机关。最终实验的统计结果如下：