LeetCode 1302. 层数最深叶子节点的和_数据结构和算法

截止到目前我已经写了 600多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

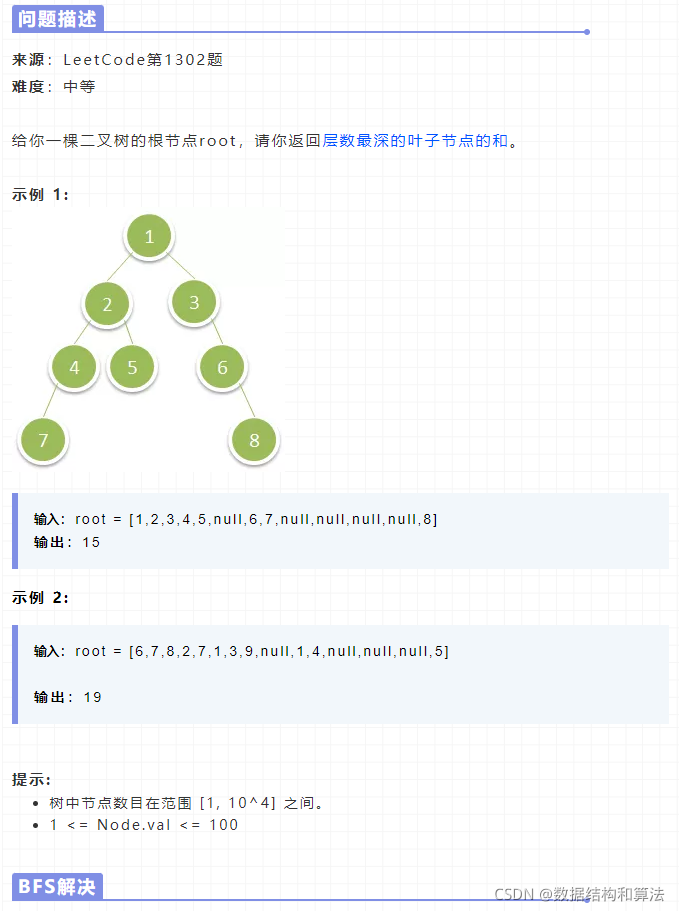
这题让求的是最深叶子节点的和，最容易想到的就BFS解决，也就是一层一层的从上往下遍历，BFS的遍历方式如下，也可以看下373，数据结构-6,树

到最后一层的时候我们再把节点的值相加即可。这里我们不知道哪一层是最深的层数，我们可以把每一层所有节点的值都相加，下一层会把上一次的给覆盖掉，最后一层下面没有了，所以没法覆盖，直接返回即可。来看下代码

public int deepestLeavesSum(TreeNode root) {
    //每层节点的和
    int res = 0;
    //队列
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    //队列不为空，继续访问队列的元素
    while (!queue.isEmpty()) {
        //当前层的节点数量
        int levelCount = queue.size();
        //当前层所有节点值的和
        res = 0;
        //遍历当前层的所有节点
        for (int j = 0; j < levelCount; j++) {
            TreeNode node = queue.poll();
            //累加当前层节点的值
            res += node.val;
            //如果左子节点不为空就把他加入到队列中
            if (node.left != null)
                queue.add(node.left);
            //如果右子节点不为空就把他加入到队列中
            if (node.right != null)
                queue.add(node.right);
        }
    }
    return res;
}

时间复杂度：O(N)，N是节点的个数，所有节点都要访问一遍
空间复杂度：O(N)，队列中存放的是每层节点的个数，满二叉树的时候最后一层节点的个数是（N+1）/2

//记录树的最大深度
private int maxLevel = 0;
//记录最后一层所有节点的和
private int sum = 0;

public int deepestLeavesSum(TreeNode root) {
    dfs(root, 0);
    return sum;
}

//level表示第几层，根节点是第0层
private void dfs(TreeNode root, int level) {
    //边界条件判断，如果是空直接返回
    if (root == null)
        return;
    //操作当前节点，如果没到最后一层，记录
    //当前访问过的最大层数，并且把sum重置为0，
    //也就是之前加的作废
    if (level > maxLevel) {
        maxLevel = level;
        sum = 0;
    }
    //如果到了最后一层，就把节点值相加
    if (level == maxLevel) {
        sum = sum + root.val;
    }
    //访问左子节点和右子节点，
    dfs(root.left, level + 1);
    dfs(root.right, level + 1);
}

时间复杂度：O(N)，N是树的所有节点个数
空间复杂度：O(H)，H是树的最大深度